Абсцисса точки м числовой единичной окружности (5 видео)

Алгебра и начала математического анализа. 10 класс

Содержание

Урок «Определение синуса и косинуса на единичной окружности»
Конспект лекций (раздаточный материал) по учебной дисциплине «Математика: Алгебра» по теме » Тригонометрические формулы» (часть 1)
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Выберите документ из архива для просмотра:
🎥 Видео

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок № 30. Определение синуса, косинуса и тангенса угла

Перечень вопросов, рассматриваемых в теме:

Ввод понятий синуса, косинуса, тангенса и котангенса угла
Определение синуса, косинуса, тангенса и котангенса угла
Решение простейших тригонометрических уравнений
Решение задач на применение знаний о синусе, косинусе, тангенсе и котангенсе в формате заданий ЕГЭ;

Глоссарий по теме

Синус угла– ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается

Косинус угла – абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается

Тангенс угла – отношение синуса угла к его косинусу.

Обозначается tg

Котангенс угла отношение косинуса угла к его синусу.

Обозначается сtg

На единичной окружности касательная, проведенная к точке (1; 0) называется линией тангенсов.

Касательная, проведенная к точке (0; 1) — линия котангенсов.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Зарождение тригонометрии относится к глубокой древности. Слово «тригонометрия» греческое: тригоно — треугольник, метрити — мера. Иными словами, тригонометрия — наука об измерении треугольников. Длительную историю имеет понятие синуса. Различные отношения отрезков треугольника и окружности встречаются уже в III в. до н. э. в работах великих математиков Древней Греции — Евклида, Архимеда, Аполлония Пергского. В IV—V вв. появился специальный термин в трудах по астрономии великого индийского ученого Ариабхаты (476 — ок.550). Отрезок он назвал ардхаджива, или более кратко джива. Арабскими математиками в IX в. слово джива было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в XII в. это слово было заменено латинским синус (sinus — изгиб, кривизна).

Косинус — это сокращение латинского выражения complementysinus, т. е. «дополнительный синус» или иначе «синус дополнительной дуги».

Название «тангенс» происходит от латинского tanger (касаться). Tangens переводится как «касающийся» (линия тангенсов — это касательная к единичной окружности).

Несмотря на то, что тригонометрия зародилась в древние времена, сегодня она охватывает практически все естественные науки и технику.

1.Найдите координаты точек А, В, С и D, лежащих на единичной окружности (рис. 1)

Рисунок 1 – единичная окружность

Поставьте в соответствие точке её координаты

Ответ: А(1; 0); В(0; 1); С(-1; 0); D(0; -1)

Сегодня на уроке мы узнаем, как по-другому называются абсцисса и ордината точки, лежащей на единичной окружности.

1.Рассмотрим окружность радиуса, равного 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют

единичной или тригонометрической.

Рисунок 2 – точка Р на единичной окружности

Точка Р (1; 0) при повороте вокруг начала координат на угол переместилась в точку Рₐ. Определим её координаты. (рис. 2).

Синусом угла называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол.

Обозначается

Косинусом угланазывается абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается

Угол может выражаться и в градусах и в радианах.

Точка А(1; 0) при повороте на угол 90 (рис. 1)

Ордината точки В равна 1, значит или

Абсцисса точки В равна 0, значит

Точка А(1; 0) при повороте на угол переместилась в точку ( рис. 1)

Найдите и

Ответ: = 0;

Точка А(1; 0) при повороте на угол переместилась в точку (рис. 1)

Найдите и

Ответ: =1= 0.

Рассмотрим ещё два понятия.

Определение. Тангенсом угла называется отношение синуса угла к его косинусу.

Обозначается tg

tg,

Найти tg 0. Вычислим по формуле tg = = 0.

Определение. Котангенсом угла называется отношение косинуса угла к его синусу.

Обозначается сtg

сtg

Найти сtg .

Вычислим по формуле сtg =

2. Меру угла(в радианах) можно рассматривать как действительное число, поэтому и – это числовые выражения. А так как каждая точка единичной окружности имеет координаты х и у такие, что выполняются неравенства -1 ≤ х ≤ 1; -1 ≤ у ≤ 1,то синус и косинус не могут превышать значения, больше .

Чтобы решить уравнения = а, нужно считать х неизвестным, число а – заданным.

Решить уравнение = 1.

Найдем точку с ординатой 1 и запишем, каким числам х она соответствует. На окружности мы видим эту точку: В (0; 1). Она соответствуют числу и всем числам вида

Решением уравнения = 1 являются х =.

3. Полезно знать синусы, косинусы, тангенсы некоторых углов. Для этого рассмотрим дугу единичной окружности в I четверти координатной плоскости (рис. 3).

Рисунок 3 – 1 четверть единичной окружности

Точки А (1; 0) и В (0; 1) нам знакомы. Рассмотрим ещё несколько точек на окружности и найдем их координаты. Точка С является серединой дуги АВ, значит угол АОС равен половине прямого угла, 45 или . Ордината точки С равна её абсциссе. Их значения нетрудно найти по теореме Пифагора из прямоугольного треугольника ОСF, оно равно А значит,

tg 45

Дуга АМ составляет третью часть прямого угла, . Ордината точки М равна , значит

, tg30.

Дуга АNсоставляет прямого угла, . Абсцисса точки N равна , поэтому

, tg 60.

Чтобы легче запомнить эти значения, придумали мнемоническое правило- правило на ладони (рис. 4).

Рисунок 4 — мнемоническое правило- правило на ладони

Расположим ладонь так, как на рисунке, пусть мизинцу соответствует угол 0, следующим пальцам– 30, 45, 60 и 90. Так же присвоим им номера: мизинец №0, следующие №1, №2, №3, №4. Чтобы найти синус, используем формулу: =. А для косинуса нумерацию будем вести от большого пальца, выполняя вычисления по той же формуле. =.

Например, =, = = .

А тангенс можно вычислить по формуле: tg = .

Тангенсы и котангенсы, также как и синусы, косинусы, можно определить по единичной окружности. Для этого познакомимся с ещё одним понятием.

На единичной окружности касательная, проведенная к точке (1; 0) называется линией тангенсов. Касательная, проведенная к точке (0; 1) — линия котангенсов (рис. 5).

Рисунок 5 – линия тангенсов и линия котангенсов

Например, чтобы найти tg, находим пересечение радиус-вектора под углом с линией тангеса. Это число , или .

Чтобы найти ctg , радиус-вектор под углом должен пересечь линию котангенсов.

Это число .

Примеры и разбор решения заданий тренировочного модуля

Решить уравнение =0.

Синусом угла является ордината точки, поэтому значения синусов находим по оси Оу.

Найдем точки А (1; 0) и С (-1; 0) с ординатой 0 и запишем, каким числам х они соответствуют. Они соответствуют числам 0 (точка А), (точка С), 2

Решением уравнения = 0 являются х =.

Z- множество целых чисел.

Решить уравнение=1.

Найдем точки с абсциссой 1 и запишем, каким числам х они соответствуют. На рис.3 мы видим эту точку: А (1; 0) Она соответствуют числу и всем числам вида

Решением уравнения= 1. являются х = , где .

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Урок «Определение синуса и косинуса на единичной окружности»

Краткое описание документа:

Видеоурок «Определение синуса и косинуса на единичной окружности» представляет наглядный материал для урока по соответствующей теме. В ходе урока рассматриваются понятия синуса и косинуса для чисел, соответствующих точкам единичной окружности, описывается множество примеров, формирующих умение решать задания, где используется данная интерпретация понятий. Удобное и понятное иллюстрирований решений, подробно описанный ход рассуждений помогают быстрее достичь целей обучения, повысить эффективность урока.

Видеоурок начинается с представления темы. В начале демонстрации дается определение синуса и косинуса числа. На экране демонстрируется единичная окружность с центром в начале координат, отмечаются точки пересечения единичной окружности с осями координат А, В, С, D. В рамке выделено определение, в котором указано, что если точке М, принадлежащей единичной окружности, соответствует некоторое число t, то абсцисса этой точки является косинусом числа t и обозначается cos t, ордината точки является синусом и обозначается sin t. Озвучивание определения сопровождается изображением на единичной окружности точки М, указанием ее абсциссы и ординаты. Представляется краткая запись с помощью обозначений, что для М(t)=M(x;y), х= cos t, у= sin t. Указываются ограничения, накладываемые на значение косинуса и синуса числа. Согласно рассмотренным данным, -1 2 +у 2 =1. Отмечается, что после подстановки вместо координат соответствующих функций, получим cos 2 t+ sin 2 t=1 – основное тригонометрическое тождество. Пользуясь способом нахождения sin t и cos t с помощью единичной окружности, заполняется таблица основных значений синуса и косинуса для чисел от 0 до 2π с шагом π/4 и для чисел от π/6 до 11π/6 с шагом π/6. На экране демонстрируются эти таблицы. С помощью их и рисунка учитель может проверить, как усвоен материал и насколько ученикам понятно происхождение значений sin t и cos t.

Рассматривается пример, в котором вычисляется sin t и cos t для t=41π/4. Решение иллюстрируется рисунком, на котором изображена единичная окружность с центром в начале координат. На ней отмечается точка 41π/4. Замечено, что данная точка совпадает с положением точки π/4. Это доказывается с помощью представления данной дроби в виде смешанной 41π/4=π/4+2π·5. Пользуясь таблицей значений косинуса, получаем значения cos π/4=√2/2 и sinπ/4=√2/2. Из полученных сведений следует, что cos 41π/4=√2/2 и sin 41π/4=√2/2.

В втором примере необходимо вычислить sin t и cos t для t=-25π/3. На экране изображается единичная окружность с отмеченной на ней точкой t=–25π/3. Сначала для решения задания число –25π/3 представляется в виде смешанной дроби, чтобы обнаружить, какому табличному значению будет соответствовать его sin t и cos t. После преобразования получаем –25π/3=-π/3+2π·(-4). Очевидно, t=-25π/3 совпадет на окружности с точкой –π/3 или 5π/3. Из таблицы выбираем соответствующие значения синуса и косинуса cos 5π/3=1/2 и sin 5π/3=-√3/2. Эти значения будут верными и для рассматриваемого числа cos (-25π/3)=1/2 и sin (-25π/3)=-√3/2. Задача решена.

Аналогично решается и пример 3, в котором необходимо вычислить sin t и cos t для t=37π. Чтобы решить пример, число 37π раскладывается, вычленяя π и 2π. В таком представлении получается 37π=π+2π·18. На единичной окружности, которая изображена рядом с решением, отмечается данная точка на пересечении отрицательной части оси ординат и единичной окружности – точка π. Очевидно, что значения синуса и косинуса числа совпадут с табличными значениями π. Из таблицы находим значения sin π=-1 и cos π=0. Соответственно, эти же значения являются искомыми, то есть sin 37π=-1 и cos 37π=0.

В примере 4 требуется вычислить sin t и cos t при t=-12π. Представляем число в виде -12π=0+2π·(-6). Соответственно, точка -12π совпадает с точкой 0. Значения косинуса и синуса этой точки sin 0=1 и cos 0=0. Эти значения и являются искомыми sin (-12π)=1 и cos (-12π)=0.

В пятом примере нужно решить уравнение sin t=√3/2. В решении уравнения используется понятие синуса числа. Так как он представляет ординату точки М(t), то необходимо отыскать точку с ординатой √3/2. На рисунке, сопровождающем решение, видно, что ординате √3/2 соответствуют две точки – первая π/3 и вторая 2π/3. Учитывая периодичность функции, отмечаем, что t=π/3+2πk и t= 2π/3+2πk для целого k.

В примере 6 решается уравнение с косинусом — cos t=-1/2. В поиске решений уравнения находим на единичной окружности точки с абсциссой 2π/3. На экране демонстрируется рисунок, на котором отмечается абсцисса -1/2. Ей соответствуют две точки на окружности — 2π/3 и -2π/3. Учитывая периодичность функций, найденное решение записывается в виде t=2π/3+2πk и t=-2π/3+2πk, где k- целое число.

В примере 7 решается уравнение sin t-1=0. Чтобы найти решение, уравнение преобразуется к виду sin t=1. Синусу 1 соответствует число π/2. Учитывая периодичность функции, найденное решение записывается в виде t=π/2+2πk, где k – целое. Аналогично в примере 8 решается уравнение cos t+1=0. Преобразуем уравнение к виду cos t=-1. Точка, абсцисса которой равна -1, соответствует числу π. Эта точка отмечена на единичной окружности, изображенной рядом с текстовым решением. Соответственно, решением данного уравнения является число t=π+2πk, где k – целое число. Не более сложным является решение уравнения cos t+1=1 в примере 9. Преобразовав уравнение, получаем cos t=0. На единичной окружности, изображенной рядом с решением, отмечаем точки –π/2 и -3π/2, в которых косинус принимает значение 0. Очевидно, решением данного уравнение будет ряд значений t=π/2+πk, где k – целое число.

В примере 10 сравниваются значения sin 2 и cos 3. Чтобы решение было наглядным, демонстрируется рисунок, где отмечены точки 2 и 3. Зная, что π/2≈1,57, оцениваем удаленность точек от нее. На рисунке отмечается, что точка 2 удалена от π/2 на 0,43, в то время как 3 удалена на 1,43, поэтому точка 2 имеет большую абсциссу, чем точка 3. Это значит, что sin 2>cos 3.

Пример 11 описывает вычисление выражения sin 5π/4. Так как 5π/4 – это π/4+π, то, используя формулы приведения, выражение можно преобразовать в вид — sin π/4. Из таблицы выбираем его значение — sin π/4=-√2/2. Аналогично в примере 12 находится значение выражения cos7π/6. Преобразуя его к виду cos(π/6+π), получаем выражение – cos π/6. Табличное значение – cos π/6=-√3/2. Это значение и будет решением.

Далее предлагается запомнить важные равенства, которые помогают в решении задач – это sin(-t)= -sin t и cos (-t)=cos t. Фактически данное выражение отображает четность косинуса и нечетность синуса. На изображении единичной окружности рядом с равенствами можно увидеть, как на координатной плоскости работают данные равенства. Также представляются два равенства, отображающие периодичность функций, важные для решения задач sin(t+2πk)= sin t и cos (t+2πk)=cos t. Демонстрируются равенства, отображающие симметричное расположение точек на единичной окружности sin(t+π)= -sin t и cos (t+π)=-cos t. Рядом с равенствами строится изоражение, на котором отображается расположение этих точек на единичной окружности. И последние представленные равенства sin(t+π/2)= cos t и cos (t+π/2)=- sin t.

Видеоурок «Определение синуса и косинуса на единичной окружности» рекомендуется применять на традиционном школьном уроке математик для повышения его эффективности, обеспечения наглядности объяснения учителя. С этой же целью материал может использоваться в ходе дистанционного обучения. Пособие также может быть полезно для формирования соответствующих навыков решения заданий у учеников при самостоятельном освоении материала.

«Определение синуса и косинуса на единичной окружности».

Дадим определение синуса и косинуса числа

ОПРЕДЕЛЕНИЕ: если точка М числовой единичной окружности соответствует числу t(тэ), то абсциссу точки М называют косинусом числа t(тэ) и обозначают cost, а ординату точки М называют синусом числа t(тэ) и обозначают sint(рис).

Значит, если М(t) = М (x ,y)(эм от тэ равно эм с координатами икс и игрек), то x = cost, y= sint (икс равен косинус тэ, игрек равен синус тэ).Следовательно, -1≤ cost ≤ 1, -1≤ sint ≤1( косинус тэ больше либо равно минус один, но меньше либо равно один ; синус тэ больше либо равно минус один, но меньше либо равно один).Зная, что каждая точка числовой окружности имеет в системе xOy свои координаты, можно составить таблицу значении синуса и косинуса по четвертям окружности, где значение косинуса положительно в первой и четвертой четвертях и, соответственно, отрицательно во второй и третьей четвертях.

Значение синуса положительно в первой и второй четвертях и, соответственно, отрицательно в третьей и четвертой четвертях. (показать на чертеже)

Так как уравнение числовой окружности имеет вид х 2 + у 2 =1( икс квадрат плюс игрек квадрат равно одному), то получаем равенство:

(косинус квадрат тэ плюс синус квадрат тэ равно единице).

Опираясь на таблицы, которые мы составляли при определении координат точек числовой окружности, составим таблицы для координат точек числовой окружности для значений cost и sint .

ПРИМЕР 1. Вычислить cos t и sin t, если t = (тэ равно сорок один пи на четыре).

Решение. Числу t = соответствует та же точка числовой окружности, что и числу , так как = ∙π = ( 10 + ) ∙π = + 2π ∙ 5( сорок один пи на четыре равно сумме пи на четыре и произведения два пи на пять). А для точки t = по таблице значение косинусов 1 имеем cos = и sin =. Следовательно,

ПРИМЕР 2. Вычислить cos t и sin t, если t = (тэ равно минус двадцать пять пи на три).

РЕШЕНИЕ: Числу t = соответствует та же точка числовой окружности, что и числу , так как = ∙ π = – (8 + )∙π = + 2π ∙ ( – 4 ) ( минус двадцать пять пи на три равно сумме минус пи на три и произведению двух пи на минус четыре). А числу соответствует на числовой окружности та же точка, что и числу . А для точки t = по таблице 2 имеем cos = и sin = .Следовательно, cos () = и sin () =.

ПРИМЕР 3. Вычислить cos t и sin t, если t = 37π; ( тэ равно тридцать семь пи).

РЕШЕНИЕ: 37π = 36π + π = π + 2π ∙ 18.Значит, числу 37π соответствует та же точка числовой окружности, что и числу π. А для точки t = π по таблице 1 имеем cos π = –1, sin π=0.Значит, cos37π = –1, sin37π=0.

ПРИМЕР 4. Вычислить cos t и sin t, если t = –12π (равно минус двенадцать пи).

РЕШЕНИЕ: – 12π = 0 + 2π ∙ ( – 6), то есть числу – 12π соответствует та же точка числовой окружности, что и числу ноль. А для точки t = 0 по таблице 1 имеем cos 0 = 1, sin 0 =0.Значит, cos( –12π) =1, sin( –12π) =0.

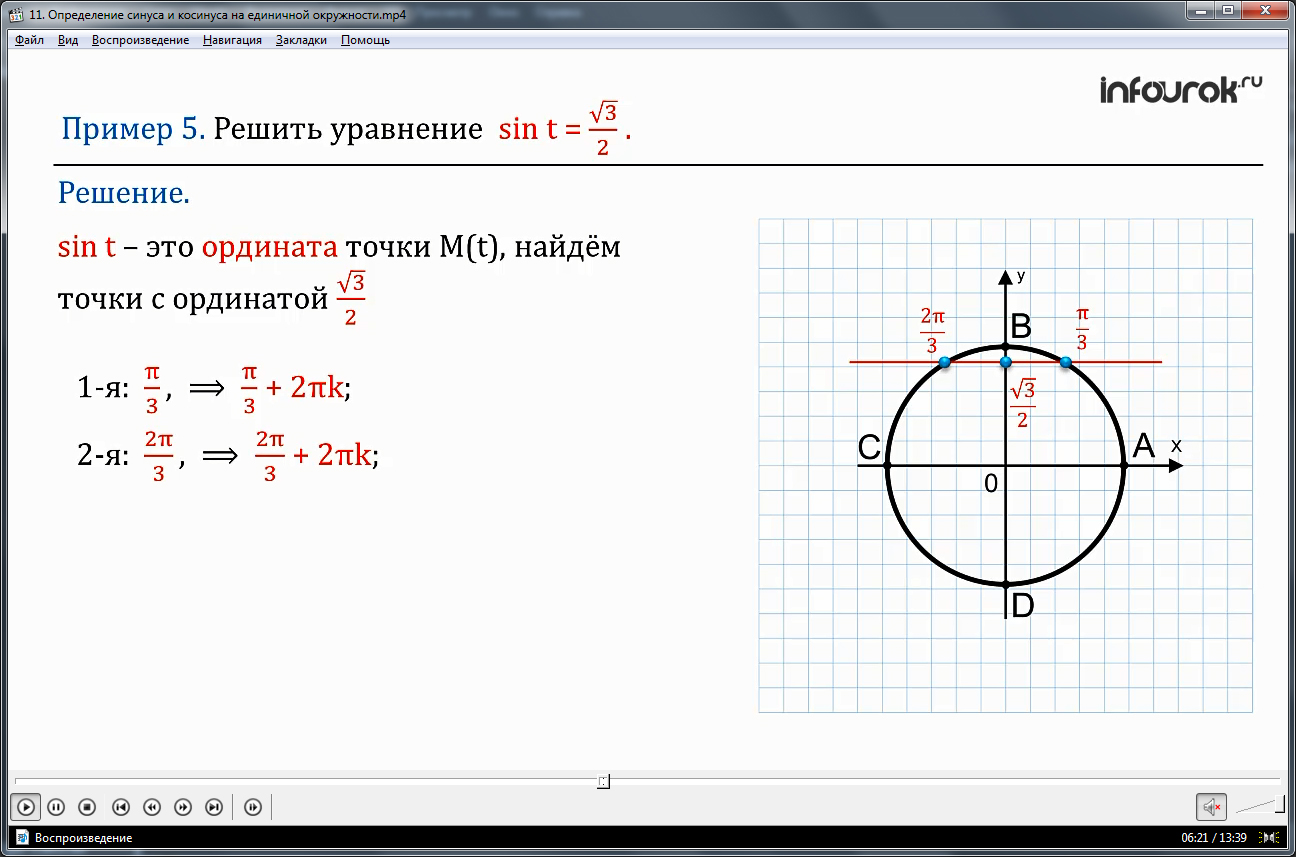
ПРИМЕР 5. Решить уравнение sin t = .

Решение. Учитывая, что sin t – это ордината точки М(t) (эм от тэ) числовой окружности, найдем на числовой окружности точки с ординатой и запишем каким числам t они соответствуют. Одна точка соответствует числу , а значит, и любому числу вида + 2πk. Вторая точка соответствует числу , а значит, и любому числу вида + 2πk. Ответ: t = + 2πk,где kϵZ (ка принадлежит зэт),t= + 2πk,где kϵZ (ка принадлежит зэт).

ПРИМЕР 6. Решить уравнение cos t = .

Решение. Учитывая, что cos t – это абсцисса точки М(t) (эм от тэ) числовой окружности, найдем на числовой окружности точки с абсциссой и запишем каким числам t они соответствуют. Одна точка соответствует числу ,а значит и любому числу вида + 2πk. А вторая точка соответствует числу или , а значит, и любому числу вида + 2πk или + 2πk.

Ответ: t = + 2πk, t=+ 2πk ( или ± + 2πk( плюс минус два пи на три плюс два пи ка) , где kϵZ (ка принадлежит зэт).

ПРИМЕР 7.Решить уравнение cos t = .

Решение. Аналогично предыдущему примеру, на числовой окружности нужно найти точки c абсциссой и записать, каким числам t они соответствуют.

По рисунку видно, что абсциссу имеют две точки Е и S, а каким числам они соответствуют мы пока не сможем сказать. К этому вопросу вернемся позже.

ПРИМЕР 8.Решить уравнение sin t = – 0,3.

Решение. На числовой окружности найдем точки с ординатой – 0,3 и запишем , каким числам t они соответствуют.

Ординату – 0,3 имеют две точки P и H, а каким числам они соответствуют мы пока не сможем сказать. К этому вопросу так же вернемся позже.

ПРИМЕР 9.Решить уравнение sin t –1 =0

Решение. Перенесем минус единицу в правую часть уравнения, получим синус тэ равно одному ( sin t =1). На числовой окружности нам нужно найти точку, у которой ордината равна один. Эта точка соответствует числу , а значит всем числам вида + 2πk( пи на два плюс два пи ка).

Ответ: t = + 2πk, kϵZ( ка принадлежит зэт).

ПРИМЕР 10.Решить уравнение cos t + 1 = 0.

Перенесем единицу в правую часть уравнения, получим косинус тэ равно минус один(cos t = – 1).Абсциссу минус один имеет точка числовой окружности, которая соответствует числу π, а это значит, и все числам вида π+2πk. Ответ: t = π+ 2πk, kϵZ.

ПРИМЕР 11. Решить уравнение cos t + 1 = 1.

Перенесем единицу в правую часть уравнения, получим косинус тэ равно нулю(cos t = 0).Абсциссу ноль имеют точки В и D (рис 1), которые соответствуют числам , , , , и т. д. Эти числа можно записать так + πk. Ответ : t = + πk, kϵZ.

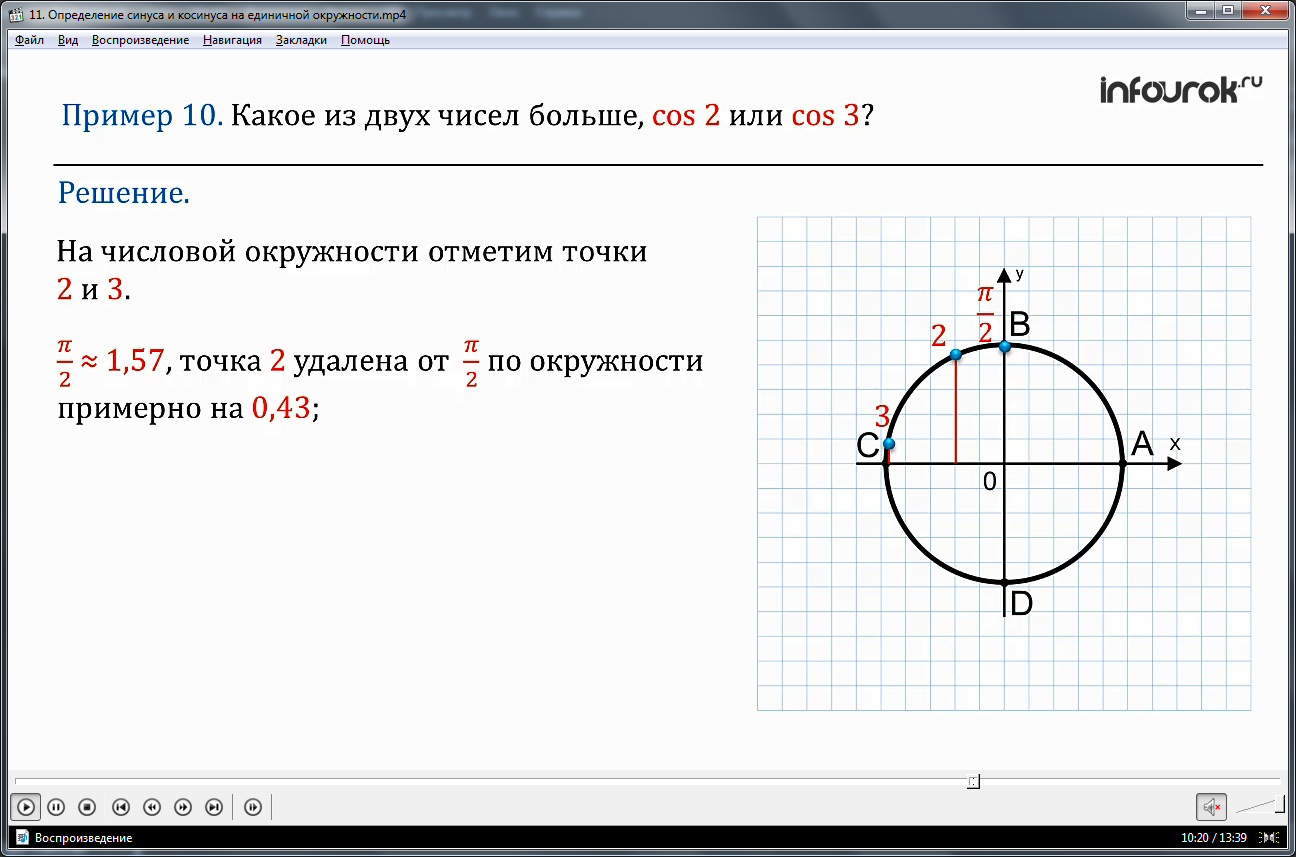
ПРИМЕР 12. Какое из двух чисел больше, cos 2 или cos 3? (косинус двух или косинус трех)

Решение. Переформулируем вопрос по-другому: на числовой окружности отмечены точки 2 и 3. У какой из них абсцисса больше?

На числовой окружности отметим точки 2 и 3. Вспомним, что .Значит, точка 2 удалена от по окружности примерно на 0,43( нуль целых сорок три сотых) ( 2 –≈ 2 – 1,57 = 0,43), а точка 3 на 1,43 (одну целую сорок три сотых). Следовательно, точка 2 находится ближе к точке , чем точка 3, поэтому у нее абсцисса больше (мы учли, что абсциссы обе отрицательные).

Ответ: cos 2 > cos 3.

ПРИМЕР 13. Вычислить sin (синус пять пи на четыре)

Решение. sin( + π) = – sin = (синус пять пи на четыре равно сумме пи на четыре и пи равно минус синус пи на четыре равно минус корень из двух на два).

ПРИМЕР 14. Вычислить cos (косинус семь пи на шесть).

cos( + π ) = – cos =. (представили семь пи на шесть как сумму пи на шесть и пи и применили третье равенство).

Для синуса и косинуса получим некоторые важные формулы.

1. Для любого значения t справедливы равенства

Синус от минус тэ равно минус синус тэ

Косинус от мину тэ равно косинусу тэ.

По рисунку видно, что у точек Е и L, симметричных относительно оси абсцисс, одна и та же абсцисса, это значит

cos(–t) = cost, но равны по модулю и противоположные по знаку ординаты (это значит sin(– t) = – sint.

2. Для любого значения t справедливы равенства

sin (t+2πk) = sin t

cos (t+2πk) = cos t

Синус от тэ плюс два пи ка равно синусу тэ

Косинус от тэ плюс два пи ка равно косинусу тэ

Это верно, так как числам t и t+2πk соответствует одна и та же точка.

3. Для любого значения t справедливы равенства

Синус от тэ плюс пи равно минус синусу тэ

косинус от тэ плюс пи равно минус косинусу тэ

Пусть числу t соответствует точка E числовой окружности, тогда числу t+π соответствует точка L, которая симметрична точке E относительно начала координат. По рисунку видно, что у этих точек абсциссы и ординаты равны по модулю и противоположны по знаку. Это значит,

4. Для любого значения t справедливы равенства

Синус тэ плюс пи на два равно косинусу тэ

Косинус тэ плюс пи на два равно минус синусу тэ.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Конспект лекций (раздаточный материал) по учебной дисциплине «Математика: Алгебра» по теме » Тригонометрические формулы» (часть 1)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Точки на числовой окружностиСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Конспект декций Тригонометрические формулы ч.1.docx

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ВОЛЖСКИЙ ИНСТИТУТ ЭКОНОМИКИ, ПЕДАГОГИКИ И ПРАВА»

Волжский социально-педагогический колледж

Математика: Алгебра (10-11кл., 1 курс СПО)

Конспект лекций (раздаточный материал) по разделу

«Тригонометрические формулы» (часть 1)

Автор: Бондаренко Людмила Валентиновна

Место работы: Волжский социально-педагогический колледж – структурное подразделение ВИЭПП

С оответствия между точками числовой прямой и точками окружности.

Пусть вертикальная прямая касается в точке Р окружности с центром О ра диуса 1 . Будем считать эту прямую числовой осью с началом в точке Р , а положительным направле нием на прямой направление вверх .

За единицу длины на числовой оси возь мем радиус окружности . Отметим на прямой несколько точек: ±1, ±3, ± π , где π 3,14 — иррациональ ное число . Вообразив эту прямую в ви де нерастяжимой нити , закрепленной на окружности в точке Р , будем мыс ленно наматывать ее на окружность. При этом точки числовой прямой с ко ординатами, например , 1, , — 1, — 2 перейдут соответственно в точки окружности М ₁ М ₂ , М ₃ , М ₄ , такие, что длина дуги PM ₁ , равна 1 , длина дуги РМ ₂ равна и т. д.

Таким образом, каждой точке прямой ставится в соответствие некоторая точка окружности.

Рассмотрим окружность радиуса R и отметим на ней дугу РМ длины R и угол РОМ.

Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан и обозначается 1 рад.

Найдем градусную меру угла в 1 радиан . Так как дуга длиной π R (полуокружность) стягивает центральный угол в 180° , то дуга длиной R стягивает угол в π раз меньший , т.е. 1 рад = 0 ; Так как π 3,14 , то 1 рад57,3°.

Если угол содержит α градусов , то его радианная мера равна α 0 = · α рад.

Применение радианной меры удобно для вычисления длины окружности , а также длины дуги .

Обычно при обозначении меры угла в радианах наименование « рад » опускают.

Поворот точки единичной окружности вокруг начала координат.

Покажем теперь, как можно установить соответ ствие между действительными числами и

Рассмотрим на координатной плоскости окруж ность радиуса 1 с центром в начале координат . Ее называют единичной окружностью ( тригонометрической окружностью ). Введем понятие поворота точки единичной окружности вокруг начала координат на угол α рад, где α — любое действительное число.

За положительное направление на единичной окружности принимают направление вращения против часовой стрелки.

За отрицательное направление на единичной окружности принимают направление вращение по часовой стрелке.

1 . Пусть α > 0 . Предположим, что точка, двига ясь по единичной окружности от точки Р (1;0) против часовой стрелки , прошла путь длиной α . Конечную точку пути обозначим М . B этом случае будем говорить, что точка М полу чена из точки Р поворотом вокруг начала коор динат на угол α рад .

2 . . Пусть α . В этом случае поворот на угол α рад означает, что движение совершалось по ча совой стрелке и точка прошла путь длиной | α |. Поворот на 0 рад означает, что точка остается месте .

Посмотрите таблицу поворотов на некоторые углы, выраженные в

* каждому действительному числу а соответствует единственная точка единичной окружности, получаемая поворотом точки Р(1;0) на угол α рад;

* одной и той же точке М единичной окружности соответствует бесконечное множество действительных чисел α + 2π k , где k — целое число , задающих поворот точки Р (1;0) в точку М .

Задача 1. Найти координаты точки, полученной поворотом точки Р ( 1;0 ) на угол: 1) 7π ; 2) — . Решение. 1).Так как 7π = π + 2π · 3 , то при повороте на 7π получается та же самая точка, что и при повороте на π , т.е. получается точка с координатами ( -1;0 ).

2).Так как — = — — 2π , то при повороте на — получается та же самая точка, что и при повороте на — , т.е. получается точка с координатами ( 0; -1 ).

Задача 2. Записать все углы, на которые нужно повернуть точку ( 1;0 ), чтобы получить точку М ; 〕 . Решение . Из прямоугольного АОМ следует, что угол АОМ равен , т.е. один из возможных углов поворота равен . Следовательно, все углы, на которые нужно повернуть точку ( 1;0 ), чтобы получить точку ; 〕 , выражаются так: + 2π k , где k — любое целое число (т.е. k = 0; 1; 2;… ).

Определение синуса, косинуса и тангенса угла

В курсе геометрии были введены определения синуса, косинуса и тангенса угла , выраженного в градусах. Вспомним эти определения :

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. sin A= a /b; sin C= c /b.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе: cos A= c /b; cos C= a /b.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему: tg A= a /c; tg C= c /a.

В тригонометрии рассматриваются произвольные углы. Как определить синус, косинус в этом случае? Рассмотрим единичную окружность, т.е. окружность с центром в начале координат и радиусом, равным 1.

Каждой точке на единичной окружности соответствует угол α , координата х и координата y .

Определение 1. Синусом угла α называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (обозначается sin α ), т.е. sin α = у

Определение 2 . Косинусом угла α называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (обозначается cos α ), т.е. cos α = х

Итак, косинус и синус — координаты точки на единичной окружности , соответствующей данному углу . Косинус — абсцисса (x), синус — ордината (y). В этих определениях угол α может выражаться как в градусах , так и в радианах .

Например , при повороте точки ( 1; 0 ) на угол , т. е. угол 90°, получается точка ( 0; 1 ). Ордината точки ( 0; 1 ) равна 1 , поэтому sin = sin 90° = 1 ; абсцисса этой точки равна 0 , поэтому cos = cos 90° = 0

Задача 3. Решить уравнение sin х = 0. Решение. Решить уравнение sin х = 0 — это значит найти все углы, синус которых равен нулю . Ординату равную нулю имеют две точки единичной окружности ( 1;0 ) и ( -1;0 ) (Рис. 1). Эти точки получаются из точки ( 1;0 ) поворотом на углы 0 , π, 2π, 3π и т.д., а также на углы — π, -2π, -3π и т.д. Следовательно sin х = 0 при х = π k , где k — любое целое числ о. Ответ можно записать х = π k , k Z .

Задача 4 . Решить уравнение cos х = 0. Решение. Абсциссу равную нулю имеют две точки единичной окружности ( 0;1 ) и ( 0;-1 ) (Рис. 3). Эти точки получаются из точки ( 1;0 ) поворотом на углы , π, + 2π и т.д., а также на углы π, — 2π и т.д. Т.е. на углы π k , k

Знаки синуса и косинуса и тангенса

Пусть точка ( 1; 0 ) движется по единичной окружности против часовой стрелки .

* Для точек , расположенных во второй четверти , ординаты положительны , а абсциссы отрицательны . Следовательно, sin α > 0 , cos α 0 , если α π .

При дальнейшем движении точки по окружности знаки синуса и косинуса определяются тем , в какой четверти окажется точка .

Если точка ( 1; 0 ) движется по часовой стрелке , то знаки синуса и косинуса также определяются тем , в какой четверти окажется точка .

Знаки тангенса. По определению

Зависимость между синусом, косинусом и тангенсом одного и того же угла

Выясним зависимость между синусом и косинусом .

Пусть точка М(х; у) единичной окружности получена поворотом точки ( 1; 0 ) на угол α .Тогда по определению синуса и косинуса х = cos α , у = sin α .

Точка М принадлежит единичной окружности , поэтому ее координаты (х; у) удовлетворяют уравнению единичной окружности х 2 + у 2 = 1 . Следовательно,

Равенство ( 1 ) выполняется при любых значениях α и называется основным тригонометрическим тождеством.

Из равенства (1) можно sin α выразить через cos α и cos α через sin α :

В этих формулах знак перед корнем определяется знаком выражения, стоящего в левой части формулы, т.е. от того, в какой четверти расположен угол.

Поэтому в формуле ( 3 ) перед корнем нужно поставить знак «+» :

Выясним теперь зависимость между тангенсом и котангенсом . По определению тангенса и котангенса .

Из равенства ( 4 ) можно выразить tg α через ctg α и наоборот:

Т.к. α π , то cos α 0 . Поэтому

Следовательно

Используя основное тригонометрическое тождеств о и определение тангенса , найдем зависимость между тангенсом и косинусом.

Получим равенство , откуда

Тангенс во второй четверти отрицателен, поэтому tg α = — .

Задача 6 . Вычислить cos α , если tg α = 3 и π α . Решение . Из формулы ( 7 ) находим Так как π α , то cos α 0 , и поэтому cos α = —

Задача 1. Доказать, что при α πk , k Z , справедливо равенство

Решение. По определению ctg α = , поэтому

Равенство ( 1 ) справедливо для всех допустимых значений входящих в него букв ( т.е. таких, при которых его левая и правая части имеют смысл,) называют тождеством, а задачи на доказательство таких равенств называют задачами на доказательство тождеств .

Задача 3 . Доказать тождество Решение . Чтобы доказать это тождество, покажем, что разность между его левой и правой частями равна нулю:

При решении задач 1—3 использовались следующие способы доказательства тождеств :

преобразование правой части к левой; преобразование левой части к правой; установление того, что разность между правой и левой частями равна нулю. Иногда удобно доказательство тождества провести преобразованием его левой и правой частей к одному и тому же выражению.

Задача 4. Доказать тождество Решение .

Тождество доказано , так как его левая и правая части равны cos 2 α — sin 2 α .

Задача 5. Упростить выражение Решение

Решение задач по теме « Тригонометрические тождества»

Используя определение тангенса, имеем

Таким образом, tg ( — α ) = — tg α . ( 3 )

Можно показать, что если α πk , k Z то ctg ( -α ) = — ctg α . Формулы ( 1 ) — ( 3 ) позволяют сводить вычисление значений синуса , косинуса и тангенса отрицательных углов к вычислению их значений для положительных углов.

Например :

sin 45 0 sin 30 0 = · — · =

sin 45 0 sin 30 0 = · + · =

Задача 3. Доказать формулы

При α = по формуле ( 2 ) получаем т.е. ( 4 )

Заменив в этой формуле β на α, получим Полагая в формуле ( 4 ) β = – α, имеем

Используя формулы ( 1 ) – ( 4 ), выведем формулы сложения для синуса :

Заменяя в формуле ( 5 ) β на – β, получаем

Задача 5. Вычислить Решение.

Для получения формулы тангенса суммы и тангенса разности достаточно применить основное тригонометрическое тождество и разделить числитель и знаменатель полученной дроби на cos α cos β , где cos α ≠ 0 и cos β ≠ 0. ( 7 )