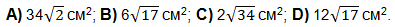Abcda1b1c1d1 параллелепипед сколько прямых параллельных прямой dc можно назвать на рисунке

Видео:Параллельность прямых. 10 класс.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Параллельные прямые в пространстве. Параллельность трех прямых

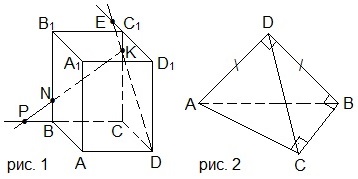
1 Дан параллелепипед. Параллельны ли прямые СК и DA ₁ ?

Выберите один из 3 вариантов ответа:

3) зависит от размеров параллелепипеда

2 Если в пространстве даны две параллельные прямые и третья прямая пересекает одну из параллельных, то пересекает ли она вторую из параллельных прямых?

Выберите один из 2 вариантов ответа:

1) не обязательно

2) обязательно пересекает

3 Сколько прямых, параллельных данной прямой, можно провести в пространстве через точку, не принадлежащую этой прямой? (в ответе укажите только число) Запишите число: ___________________________

4 В основании прямоугольного параллелепипеда ABCDA ₁ B ₁ C ₁ D ₁ лежит квадрат со стороной 1 см, а длина бокового ребра параллелепипеда равна 3 см. Точки P, T, O и K являются серединами отрезков AB, B B ₁ , B ₁ D и AD соответственно. Вычислите периметр четырехугольника PTOK.

Выберите один из 5 вариантов ответа:

1) 2) 3)

4) 5)

ABCDA ₁ B ₁ C ₁ D ₁ — параллелепипед. Сколько прямых, параллельных прямой DC , можно назвать на рисунке. В ответе укажите только число.

Запишите число: ___________________________

6 Если в пространстве даны две параллельные прямые и одна из них пересекает некоторую плоскость, то пересекает ли эту плоскость другая параллельная прямая?

Выберите один из 3 вариантов ответа:

1) нет 2) не обязательно 3) да

7 Если взять ребро куба, то сколько других ребер ему параллельны? (в ответе укажите только число) Запишите число: ___________________________

8 Сколько существует вариантов взаимного расположения двух различных прямых в пространстве?

Выберите один из 3 вариантов ответа:

9 Дан куб. Какие из указанных ниже пар ребер — параллельны?

Выберите несколько из 4 вариантов ответа:

1) 2)

3) 4)

10 Дан параллелепипед. Параллельны ли прямые АК и DM ?

Выберите один из 3 вариантов ответа:

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Г10(I)-4. Тетраэдр и параллелепипед

Геометрия 10 класс. Глава I. Тест 4.

Вариант 1.

1. Выбрать верные утверждения.

1) Грани тетраэдра – это треугольники, из которых состоит тетраэдр.

3) Диагональю параллелепипеда называется отрезок, соединяющий две вершины любой грани.

4) Сечением тетраэдра могут быть только треугольники и четырёхугольники, так как тетраэдр имеет 4 грани.

5) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.

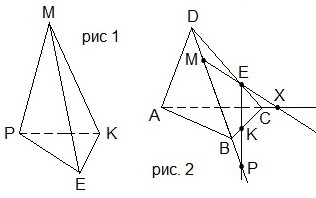
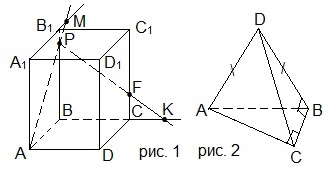
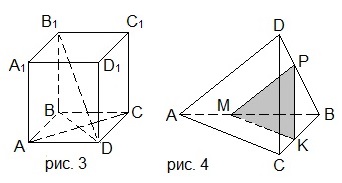
2. Назвать все пары скрещивающихся рёбер тетраэдра MPEK на рисунке 1.

A) MP и KE; MK и PE; ME и PK; B) MP и PE; MK и PE; ME и PK;

C) MP и KE; MK и KE; ME и PK; D) MP и KE; MK и PE; ME и EK.

3. Выбрать верные утверждения, используя рисунок 2.

1) Х – точка пересечения прямой МЕ и плоскости АВС.

2) Р – точка пересечения прямой ЕК и плоскости АВD.

3) Точки Х и Р лежат в одной плоскости.

A) 2 и 3; B) 1 и 3; C) 1 и 2; D) 1; 2 и 3.

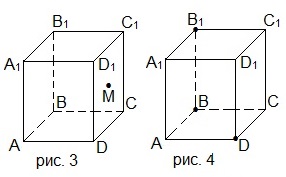
4. На рисунке 3 точка М принадлежит боковой грани CC₁D₁D прямоугольного параллелепипеда ABCDA₁B₁C₁D₁. Через точку М проведите сечение параллелепипеда плоскостью, параллельной плоскости АВС. Найдите площадь этого сечения, если АВ=5 см, AD=7 см, AA₁=9 см.

A) 45 см 2 ; B) 35 см 2 ; C) 63 см 2 ; D) 21 см 2 .

5. Основанием параллелепипеда ABCDA₁B₁C₁D₁ на рисунке 4 является квадрат со стороной 10 см и боковым ребром, равным 12 см. Угол B₁BD – прямой. Проведите сечение параллелепипеда через точки B, D и В₁ и найдите площадь этого сечения.

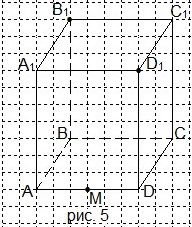
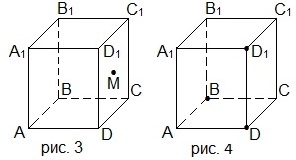
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки B₁, D₁ и М. Какая фигура получилась в сечении?

A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.

Вариант 2.

1. Выбрать верные утверждения.

1) Поверхность, составленная из четырёх треугольников, называется тетраэдром.

2) Два ребра тетраэдра, не имеющие общих вершин, называют смежными.

3) Грани параллелепипеда – это параллелограммы, из которых составлен параллелепипед.

4) Секущей плоскостью параллелепипеда называют любую плоскость, по обе стороны от которой имеются точки данного параллелепипеда.

5) Две грани параллелепипеда, имеющие общие рёбра, называются противоположными.

A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.

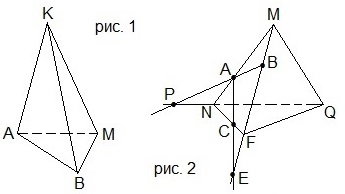
2. Назвать все пары скрещивающихся рёбер тетраэдра KABM на рисунке 1.

A) AK и AB; BK и AM; MK и AB; B) AK и BM; BK и AB; MK и AB;

C) AK и BM; BK и AM; MK и AB; D) AK и BM; BK и AM; MK и MB.

3. Выбрать верные утверждения, используя рисунок 2.

1) Р – точка пересечения прямой АВ и плоскости NMQ.

2) E – точка пересечения прямой AC и плоскости MFQ.

3) Точки E и Р лежат в различных плоскостях.

A) 1; 2 и 3; B) 1 и 3; C) 1 и 2; D) 2 и 3.

4. На рисунке 3 точка М принадлежит боковой грани CC₁D₁D прямоугольного параллелепипеда ABCDA₁B₁C₁D₁. Через точку М проведите сечение параллелепипеда плоскостью, параллельной плоскости АА₁D₁. Найдите площадь этого сечения, если АВ=5 см, AD=7 см, AA₁=9 см.

A) 45 см 2 ; B) 35 см 2 ; C) 63 см 2 ; D) 21 см 2 .

5. Основанием параллелепипеда ABCDA₁B₁C₁D₁ на рисунке 4 является квадрат со стороной 8 см и боковым ребром, равным 7 см. Угол B₁BD – прямой. Проведите сечение параллелепипеда через точки B, D и D₁ и найдите площадь этого сечения.

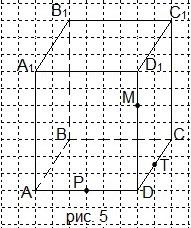
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и Т. Какая фигура получилась в сечении?

A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.

Вариант 3.

1. Выбрать верные утверждения.

1) Тетраэдр имеет 4 грани, 6 рёбер и 4 вершины.

2) Параллелепипед имеет 6 граней, 12 рёбер и 8 вершин.

3) Противоположные грани параллелепипеда параллельны и равны.

4) Секущей плоскостью тетраэдра называют любую плоскость, по одну сторону от которой имеются точки данного тетраэдра.

5) Секущая плоскость пересекает грани параллелепипеда по отрезкам-рёбрам параллелепипеда. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда.

A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.

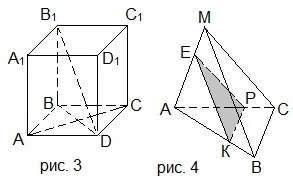
2. Выбрать верные утверждения, используя рисунок 1.

1) M – точка пересечения прямой АP и плоскости A₁B₁C₁.

2) K – точка пересечения прямой PF и плоскости ABD.

3) Точки M и K лежат в одной плоскости.

A) 1; 2 и 3; B) 1 и 3; C) 2 и 3; D) 1 и 2.

3. В тетраэдре DABC на рисунке 2 угол ADB равен 60°, углы АСВ и CBD прямые, AD=BD, АВ=26, DC=31. Найти АС. В ответе записать квадрат получившегося значения.

A) 391; B) 625; C) 380; D) 576.

4. Основанием параллелепипеда ABCDA₁B₁C₁D₁ на рисунке 3 является квадрат со стороной 4 см и боковым ребром, равным 6 см. Угол B₁BD – прямой. Проведите сечение параллелепипеда через прямую АС параллельно B₁D и найдите площадь этого сечения.

5. В тетраэдре МАВС на рисунке 4 проведено сечение КЕР параллельно грани ВСМ. Площадь треугольника ВСМ равна 60 см 2 . Найти площадь треугольника КЕР, если АК:КВ=7:3.

A) 29,4 см 2 ; B) 58,8 см 2 ; C) 294 см 2 ; D) 30,4 см 2 .

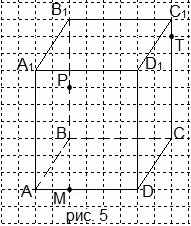
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и Т. Какая фигура получилась в сечении? A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.

Вариант 4.

1. Выбрать верные утверждения.

1) Две грани параллелепипеда, имеющие общее ребро, называются смежными.

2) Все рёбра параллелепипеда называются боковыми рёбрами.

3) Секущая плоскость пересекает грани тетраэдра по отрезкам прямых, содержащих рёбра тетраэдра. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.

4) Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники, так как параллелепипеда имеет 6 граней.

5) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.

2. Выбрать верные утверждения, используя рисунок 1.

1) Р – точка пересечения прямой NK и плоскости ACD.

2) E – точка пересечения прямой DK и плоскости A₁B₁C₁.

3) Точки E и Р лежат в различных плоскостях.

A) 2 и 3; B) 1 и 3; C) 1; 2 и 3; D) 1 и 2.

3. В тетраэдре DABC на рисунке 2 углы АСВ, АDВ и CBD — прямые, AD=BD=8, DC=11. Найти АС. В ответе записать квадрат получившегося значения.

A) 72; B) 71; C) 57; D) 64.

4. Основанием параллелепипеда ABCDA₁B₁C₁D₁ на рисунке 3 является квадрат со стороной 6 см и боковым ребром, равным 8 см. Угол B₁BD – прямой. Проведите сечение параллелепипеда через прямую АС параллельно B₁D и найдите площадь этого сечения.

5. В тетраэдре DАВС на рисунке 4 проведено сечение MPK параллельно грани АDС. Площадь треугольника МРК равна 4 см 2 . Найти площадь треугольника АDС, если СК:ВК=3:5.

A) 10,24 см 2 ; B) 20,48 см 2 ; C) 6,4 см 2 ; D) 8,64 см 2 .

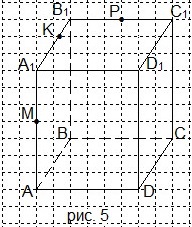
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и К. Какая фигура получилась в сечении? A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.

1) Поверхность, составленная из четырёх треугольников, называется тетраэдром.

2) Грани тетраэдра – это треугольники, из которых состоит тетраэдр.

3) Тетраэдр имеет 4 грани, 6 рёбер и 4 вершины.

4) Два ребра тетраэдра, не имеющие общих вершин, называют противоположными.

6) Грани параллелепипеда – это параллелограммы, из которых составлен параллелепипед.

7) Параллелепипед имеет 6 граней, 12 рёбер и 8 вершин.

8) Две грани параллелепипеда, имеющие общее ребро, называются смежными.

9) Две грани параллелепипеда, не имеющие общих рёбер, называются противоположными.

10) Диагональю параллелепипеда называется отрезок, соединяющий две вершины, не принадлежащие одной грани.

11) Рёбра параллелепипеда, не принадлежащие основаниям, называются боковыми рёбрами.

12) Противоположные грани параллелепипеда параллельны и равны.

13) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

14) Секущей плоскостью тетраэдра называют любую плоскость, по обе стороны от которой имеются точки данного тетраэдра.

15) Секущей плоскостью параллелепипеда называют любую плоскость, по обе стороны от которой имеются точки данного параллелепипеда.

16) Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.

17) Секущая плоскость пересекает грани параллелепипеда по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда.

18) Сечением тетраэдра могут быть только треугольники и четырёхугольники, так как тетраэдр имеет 4 грани.

19) Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники, так как параллелепипеда имеет 6 граней.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллелепипед. Свойства граней и диагоналей параллелепипеда

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы дадим определение параллелепипеда, обсудим его строение и его элементы (диагонали параллелепипеда, стороны параллелепипеда и их свойства). А также рассмотрим свойства граней и диагоналей параллелограмма. Далее решим типовую задачу на построение сечения в параллелепипеде.

📸 Видео

№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

№114. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте на ребре АВ точку М. Постройте сечение паралСкачать

№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

№110. Докажите, что в параллелепипеде ABCDA1B1C1D1 плоскость A1DB параллельна плоскости D1CB1.Скачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

Параллельность прямой и плоскости. 10 класс.Скачать

№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Объем параллелепипеда ABCDA_1B_1C_1D_1 равен 9. Найдите объем треугольной пирамиды ABCA_1.Скачать

№76. Дан параллелепипед ABCDA1B1C1D1. Докажите, что AC||A1C1 и BD||B1D1.Скачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

№83. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей черезСкачать

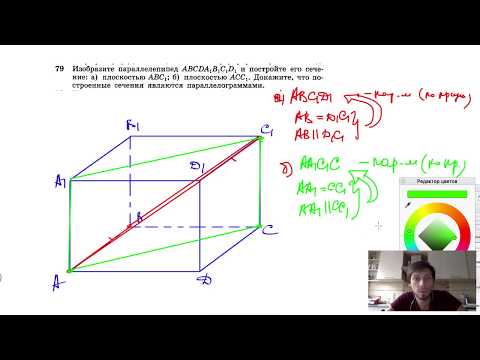
№79. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью АВС1;Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

№82. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте внутреннюю точку М грани АА1В1ВСкачать