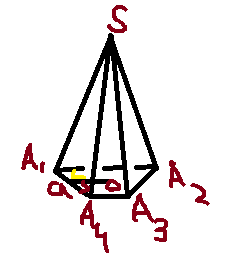
Условие
Дано:
А1А2А3А4 – трапеция
А1А4=А2А3 = а
О –центр окружности, вписанной в А1А2А3А4
ОL–радиус описанной окружности
Найти:
Vпирамиды – ? 
Решение
Рассмотрим основание пирамиды. Первым делом нам надо найти площадь основания. Высота трапеции h=2r, ребро равно a. Синус угла между боковой стороной и основанием sinальфа = 2r/a
По формуле 4r^2/sinальфа находим площадь основания
C имеющимися данными невозможно найти высоту пирамиды, а значит и объем пирамиды тоже. А так получилось бы
V = (1/3) * (4r^2/sinальфа) * H, где H высота пирамиды
Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать
Простейшие задачи на применение теоремы о трех перпендикулярах, на угол между прямой и плоскостью
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный видеоурок посвящен теме «Простейшие задачи на применение теоремы о трех перпендикулярах, на угол между прямой и плоскостью». В начале урока мы повторим материал о перпендикулярах, их геометрические свойствах.Вспомним терминологию, доказательство теоремы о трех перпендикулярах. Затем решим несколько простейших задач с применением этой теоремы на угол между прямой и плоскостью.
Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать
Контрольная работа по математике
Контрольная работа по математике.
2 курс.1 семестр.
Образец решения задач
Задача 1. Дано: АА1 – перпендикуляр,
АВ и АС – наклонные, Ð АВС = 90°, Ð АСА1 = 30°,
1. Рассмотрим DСАА1:
Ð А1 = 90°, т. к. АА1^ плоскости α
Ð С = 30°, АС – гипотенуза. АС = 2, АА1=2×2=4
2. Рассмотрим DАВС:
Ð С = 90°(по условию), по теореме Пифагора АВ2=ВС2+АС2, АВ=
=5
3. В DАВС СМ – высота
Пусть ВМ = х, то АМ = 5-х
СМ2=СВ2 – ВМ2; СМ2 = 9-х2 в DСВМ
СМ2=АС2 – АМ2; СМ2 = 16-(5-х2 ) в DАСМ
9-х2=16-(5-х)2; 9-х2=16-25+10х-х2;10х=18; х=1,8
ВМ = 1,8; то АМ = 5-1,8 = 3,2
СМ2=16-(3,2)2=16-10,24=5,76; См = 2,4
Задача №2
Дано: MN – проекция отрезка АВ на плоскость α,
1. Построим АК|| MN
Рассмотрим DАDP и DАВК,
Ð А – общий,
ÐР = ÐК, т. к. АК || MN
4. 
DE = DP – EP = 12 – 8 = 4
Ответ: DE = 4
Задача 3. Дано: АВ – перпендикуляр к плоскости α,
2. Рассмотрим DАВD: АB^BD, т. к. АB^ α
Ð D = 60° Þ Ð A = 30°
AD= AB:sin 60° = 1 : 
= 
3. Рассмотрим DАВC: АB^BC, т. к. АB^ α
АB = 1 (лежит против угла в 30°) Þ АС = 2 АВ = 2
ВС = 1 × ctg 30° = 
4. DАВD: ВD = 
= 
5. DВCD: CD= 
= 
6. P = 
Ответ: Р= 
Задача 4. Дано: АВ – перпендикуляр,
АС и АD – наклонные, DCBD – равносторонний АВ = ВС = BD
Найдите: 
1. Пусть ВС = BD= CD = АВ = а
2. D АВС = DАBD т. к. АB^ α, то АB^BD и АB^BC и АВ = BD; АВ = BC Þ АC = AD
3. по теореме Пифагора AC = 
4. P DAСD=AC +AD +CD; P DAСD= 
5. DCВD – равносторонний, т. к. ВС = CD = BD, то r = 
6. 
Ответ:
Задача 5. Основания равнобедренной трапеции равны 10 см и 34 см. высота – 32 см. Через большее основание проведена плоскость α, образующая с высотой трапеции угол в 60°. Определить проекцию боковой стороны трапеции на плоскость α.
АD= 34 см BС = 10 см, BK= 32 см, ADÎ α, Ð BKO = 60°
Найдите: AO – проекция наклонной АВ/
1. Рассмотрим АBСD – трапецию D АВК: АК=
=12
2. D АВK: 
3. D ВОК: BO^ αÞ BO^ KO, Ð BKO = 60°, BO= BK sin 60° = 32 
4. D АВO: BO^ α Þ BO^ AO, AO= 
Вариант 1
1. Дано: АВ – перпендикуляр, АС и AD – наклонные,
 |
2. Дано: КМ– проекция отрезка АВ на плоскости a,
АМ=2, ВС:АС =1:4
3. Из концов отрезка АВ, параллельного плоскости a, проведены наклонные АС и BD, проекции которых на плоскость соответственно равны 3 см и 9 см и лежат по разные стороны от проекции отрезка АВ. Найти расстояние между основаниями наклонных, если АВ =16 см и АС ^ АВ, ВD ^ АВ. Сделайте чертеж.
4. Из точки пространства проведены к данной плоскости перпендикуляр, равный 6, и наклонная длиной 9. Найдите проекцию перпендикуляра на наклонную.
 |
1. Дано: АВ – перпендикуляр,
АС и AD – наклонные к плоскости a,
Ð АСВ = Ð АDВ =30°, СD = 
АВ.
 |
2. Дано: DАВС, D – точка в пространстве,
DA = DC, DO ^ (ABC)
3. Прямые АВ и CD расположены по разные стороны от плоскости a и параллельны прямой EF, лежащей в этой плоскости. Найти расстояние между прямыми АВ и CD, если они удалены от прямой EF соответственно на 17 см и 25 см, а их проекции от той же прямой – на 15 см.
4. Сторона равностороннего треугольника равна 3. Найдите расстояние от его плоскости до точки, которая отстоит от каждой из его вершин на 2.
Вариант 3
1. Дано: АВ – перпендикуляр, АС и AD – наклонные,
Ð АСВ = 45°, АС =
16, BD = 6.
 |
2. Дано: DE– проекция отрезка АВ на плоскости a,
АD=6, АС =12, ВЕ = 2.
3. В точках А и В плоскости a восстановлены к ней перпендикуляры АС =2,4 см и BD = 12 см. Через концы перпендикуляров проведены прямая DE до пересечения в точке Е с плоскостью a. Найти длину отрезка DE, если расстояние между перпендикулярами равно 28 см. Сделайте чертеж.
4. К данной плоскости проведены две равные наклонные; угол между ними равен
60°, а угол между их проекциями – прямой. Найдите расстояние от данной точки до плоскости.
Вариант 4
2. Дано: DАВС, Ð ACB =90°,
О – центр описанной окружности,
АМ = МC, OD ^ (ABC), АВ = 5,
АС = 3, DO = 2
3. Даны плоскость a и DАВС. Сторона АВ параллельна плоскости a, а продолжения сторон АС и ВС пересекают плоскость a в точках D и Е. Определить DE, если АВ = 15 см и расстояние точек А и С от плоскости равны соответственно 6 см и 18 см.
4. К данной плоскости проведены две равные наклонные; угол между ними равен
60°, а угол между их проекциями – прямой. Найдите угол между каждой наклонной и ее проекцией.
Вариант 5
1. Дано: CD – проекция отрезка АВ на плоскостьa,
 |
3. Равнобедренная трапеция расположена на плоскости так, что основания ее параллельны плоскости. Проекция трапеции на плоскость a есть также трапеция описанная около круга. Определить угол между боковой стороной данной трапеции и перпендикуляров к плоскости a, если основания трапеции равны 2 дм и 6 дм, а боковая сторона 8 дм. Сделайте чертеж.
4. 
В равнобедренном треугольнике основание и высота равны по 4. Данная точка находится на расстоянии 6 от плоскости треугольника и на равном расстоянии от его вершин. Найдите это расстояние.
1. Дано: DАВС, О – центр вписанной окружности,
ОD^(АВС),
АС = ВС – 5, АВ =6, DО = 1, АМ = МВ.
 |
3. Ромб, высота которого равна 
и острый угол равен 60°, лежит одной стороной на плоскости a. Проекция ромба на эту плоскость есть четырехугольник, один из углов которого равен 45°. Найти площадь этого четырехугольника и расстояние второй стороны ромба от плоскости a.
4. Катеты прямоугольного треугольника АВС равны 3 и 4. Из вершины прямого угла С проведен к плоскости этого треугольника перпендикуляр CD=1. Найдите расстояние от точки D до гипотенузы AB.
Вариант 7
1. Дано: АВ – перпендикуляр, АС = AD – наклонные,
Ð АСВ = 60°, АС =4, BD = 
.
3. Определить форму сечения треугольной пирамиды плоскостью, параллельной двум скрещивающимся ребрам, если эти ребра взаимно перпендикулярны. Сделайте чертеж.
4. 
Стороны треугольника относятся как10:17:21, а его площадь равна 84. Из вершины большего угла этого треугольника проведен перпендикуляр к его плоскости, равный 15. Найдите расстояние от его концов до большей стороны.
1. Дано: АВ – перпендикуляр к плоскости a,
АС и AD – наклонные,
Ð АСВ = Ð АDВ =30°, Ð САD = 60°,
R= 
( радиус окружности, описанной
около треугольника АСD).
 |
Найдите: S– площадь круга, описанного вокруг DАВС.
3. Дана правильная четырехугольная пирамида SABCD. Через точку М, делящую сторону АВ основания в отношении 1:3, провели плоскость, параллельную стороне AD основания и боковому ребру SB. Вычислить площадь сечения, если AD = 36 см и SB = 30 см.
4.К вершине А прямоугольника ABCD проведен к его плоскости перпендикуляр АМ, конец М которого отстоит от других вершин на расстоянии 6, 7, и 9. Найти длину перпендикуляра АМ.
 |
1. Дано: АВ – перпендикуляр, АС и AD – наклонные,
2. Дано: КМ– проекция отрезка АВ на плоскости a,
АМ=2, ВС:АС = 1:4
3. Из концов отрезка АВ, параллельного плоскости проведены наклонные АС и BD, перпендикулярные отрезку АВ, проекции которых на плоскость соответственно равны 3 см и 9 см и лежат по разные стороны от проекции отрезка АВ. Найти расстояние между основаниями наклонных, если АВ = 16 см. Сделайте чертеж.
4. Высота правильной четырехугольной пирамиды равна 
, апофема наклонена к плоскости основания под углом 30°. Найдите боковые ребра.
Вариант 10
1. Дано: АВ – перпендикуляр,
АС и AD – наклонные к плоскости a,
Ð АСВ = Ð АDВ =30°, СD =АВ.
 |
3. Прямые АВ и CD расположены по разные стороны от плоскости a и параллельны прямой EF, лежащей в этой плоскости. Найти расстояние между прямой АВ и CD, если они удалены от прямой EF соответственно на 17 см и 25 см, а их проекции от той же прямой – на 15 см.
4. В параллелограмме АВCD вершина А и D находятся на плоскости М, а В и С – вне ее. Сторона AD = 10, сторона АВ = 15, проекции диагоналей АС и DD на плоскость М соответственно равны 13,5 и 10,5. Найдите диагонали.
🎦 Видео
Задача из Третьяковки ★ Пример на устный счёт ★ (10^2+11^2+12^2+13^2+14^2)/365Скачать
№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать
2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать
№975. Найдите координаты точек пересечения прямой 3x-4y + 12 = 0 с осями координатСкачать
ЕГЭ Математика Задание 6#27935Скачать
Алгебра 10 класс. 17 сентября. Числовая окружность #3Скачать
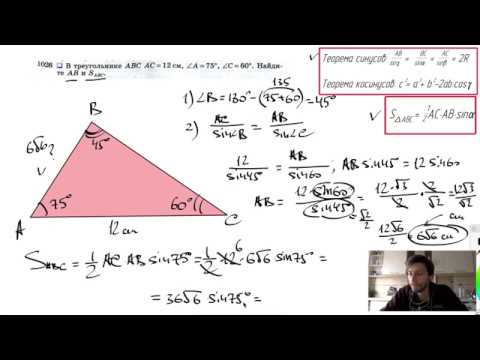
№1026. В треугольнике ABC АС = 12 см, ∠A= 75°, ∠C=60°. Найдите АВ и SABCСкачать
2 вариант ЕГЭ Ященко 2023 математика профильный уровень 🔴Скачать
Новое 10 задание легко! и без формулы БернуллиСкачать
№321. Измерения прямоугольного параллелепипеда ABCDA1B1C1D1 таковы:Скачать
В треугольнике ABC на сторонах АВ и ВС отмечены точки М и К соответственно, ВМ/АВ = 1/2, ВК/ВС = 4/5Скачать
Математика 2 класс (Урок№3 - Счёт десятками. Образование и запись чисел от 20 до 100.)Скачать
Один плюс одинСкачать
2+2=5?Скачать
№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать
Сложение и вычитание в пределах 20. Устный счет. 1 и 2 классСкачать
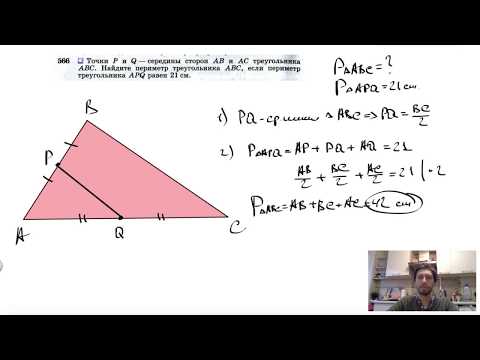
№566. Точки Р и Q — середины сторон АВ и АС треугольника ABC. Найдите периметр треугольникаСкачать
№264. Высоты АА1 и ВВ1 треугольника ABC пересекаются в точке М. Найдите ∠AMB, еслиСкачать
