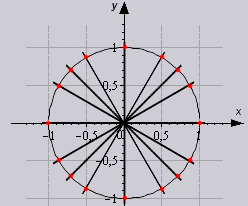
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
- А теперь подробно о тригонометрическом круге:
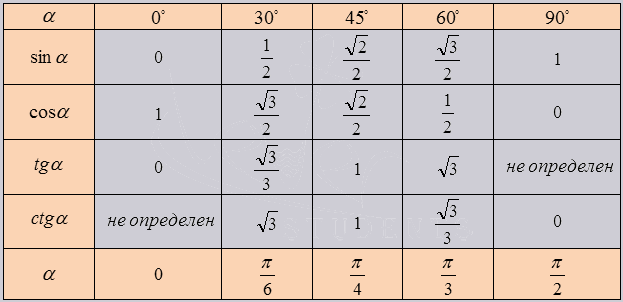
- Тригонометрическая таблица
- Таблица синусов, косинусов, тангенсов и котангенсов!
- Деление окружности на градусы
- Содержание
- Градус [ править | править код ]
- Минуты и секунды [ править | править код ]
- Угловая секунда [ править | править код ]
- Использование [ править | править код ]
- Дольные единицы [ править | править код ]
- 🎥 Видео
Видео:10 класс, 11 урок, Числовая окружностьСкачать

А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Тригонометрическая таблица
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90. 360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, котангенс от 0 0 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
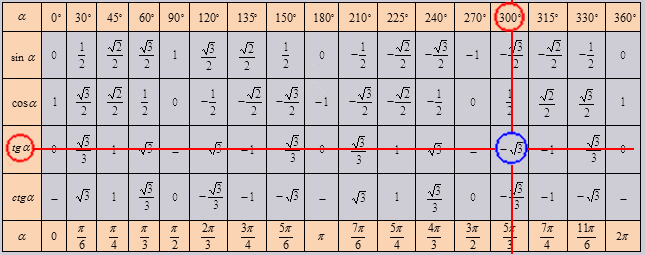
Изобразим все полученные значения в виде тригонометрической таблицы:
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

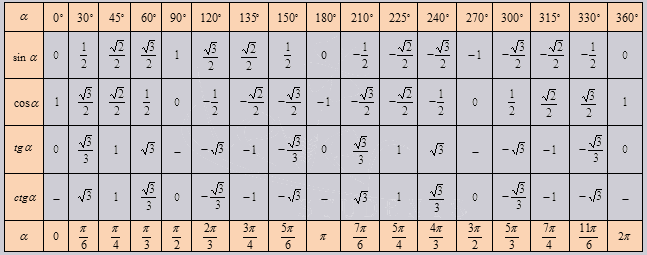
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z . 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
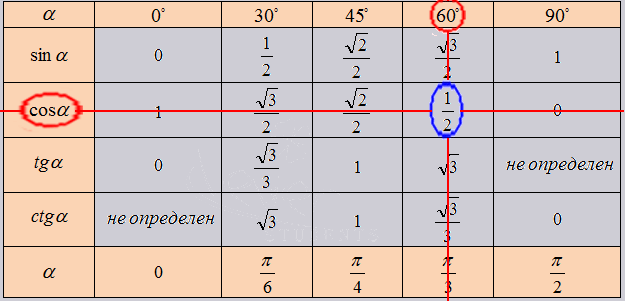
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
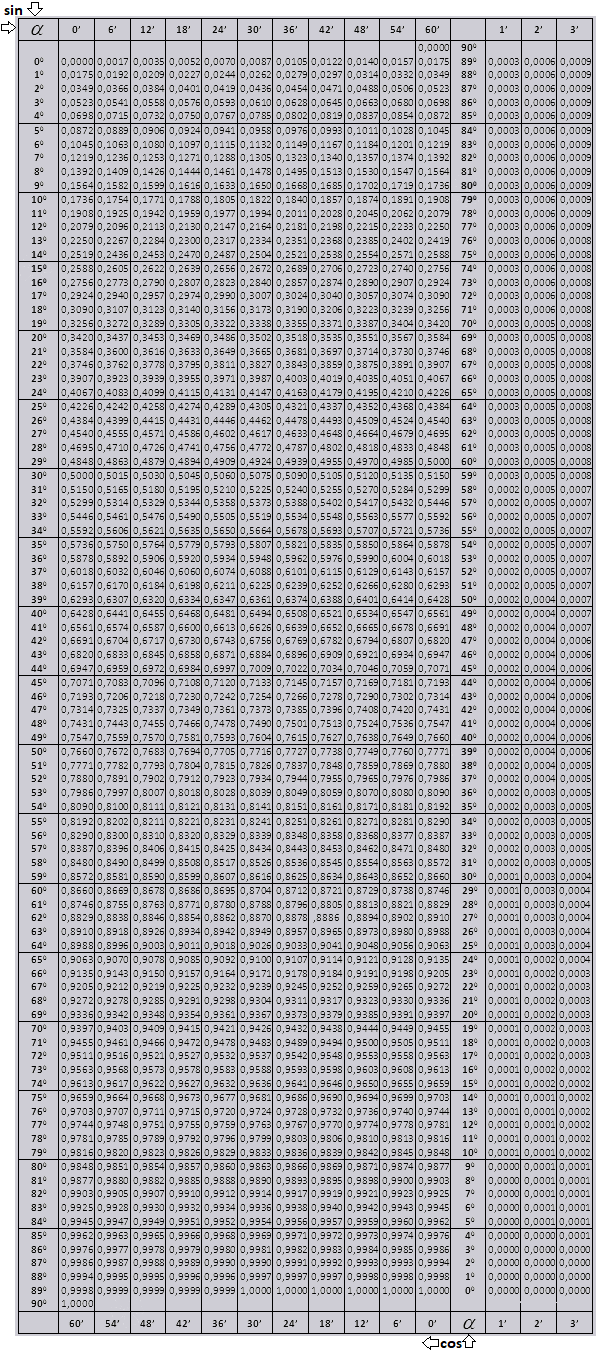
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
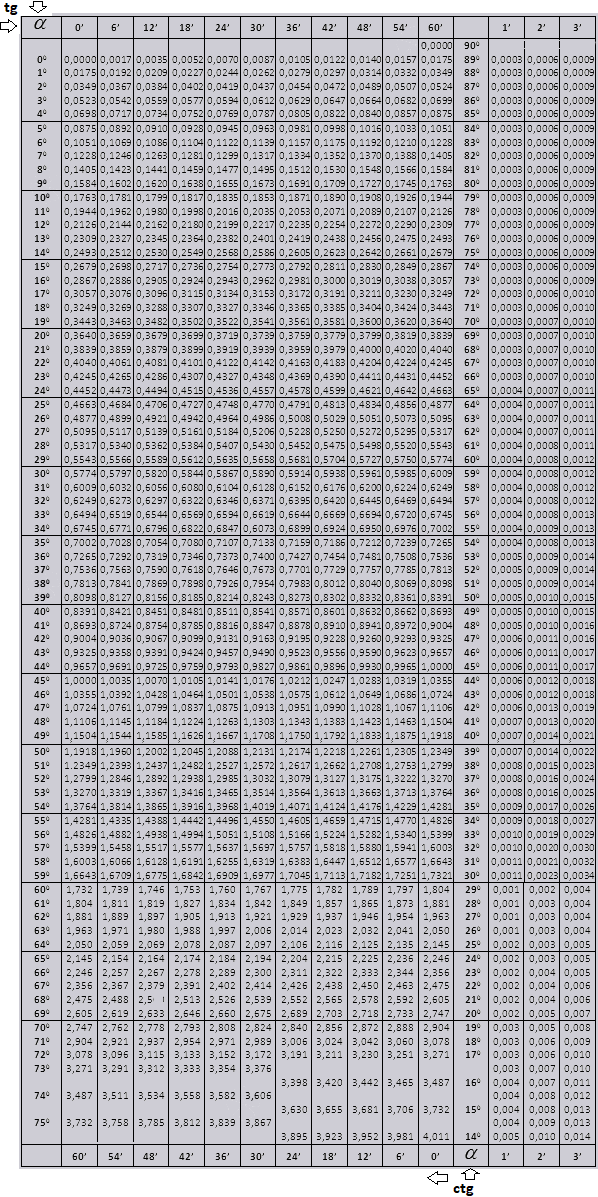
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
tg угла начиная с 0 0 заканчивая 76 0 , ctg угла начиная с 14 0 заканчивая 90 0 .
tg до 90 0 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.

При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054

При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397

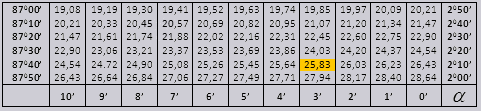
Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
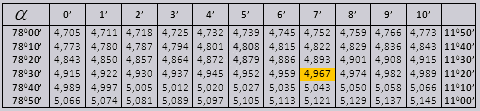
а ctg 20 0 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Видео:ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Деление окружности на градусы
Во всем мире принято странное деление окружности на 360 градусов. Со всех точек зрения было бы логичнее деление окружности на 2, потом на 4, потом на 8, 16, 32, 64 и т. д. части. А то поди ж ты: сначала делим окружность на 4 части, потом каждую четверть на 90 градусов. Почему на 90? Почему не на 100 или 120? Оказывается, деление окружности на 360 градусов ведет свое начало от вавилонских жрецов. Они, наблюдая за движением Солнца, обнаружили, что в день равноденствия Солнце от восхода до заката описывает на небесном своде полуокружность, в которой видимый поперечник Солнца укладывается ровно 180 раз. Поэтому-то они и стали каждую полуокружность делить на 180 частей, а каждую окружность – на 360 градусов! Школьный транспортир напоминает, что каждое его деление есть не что иное, как отпечаток – след Солнца, проходящего по небосклону в день равноденствия.
Существует, правда, египетская гипотеза происхождения деления окружности. Длительность года у египтян составляла 360 дней. Год был разбит на 12 месяцев, а каждый месяц на 30 дней. И Солнце по небу проходило каждый год через 12 зодиакальных созвездий. Так что Солнце находилось в каждом из этих созвездий по 30 дней. Итак, за 1 день солнце проходит по небу расстояние в 1 единицу пути. Таких единиц всего 360. И только потом эту единицу пути назвали градусом.
Герой романа Жюля Верна «Таинственный остров» инженер Сайрес Смит, чтобы определить величину острого угла, образованного ножками самодельного циркуля, «измерил этот угол по окружности, разделённой на триста шестьдесят равных частей; угол равнялся десяти градусам». Зачем для измерения острого угла потребовалось делить на части всю окружность, когда достаточно рассмотреть её четверть, непонятно, и как удалось добиться их равенства? Поэтому, деление окружности непростой вопрос, которому во многих задачах стоит уделить время.
Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
Видео:Длина дуги окружности. 9 класс.Скачать

Содержание
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Градус [ править | править код ]
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году [1] . Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.
Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления [2] [3] .
Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.
Градус в альтернативных единицах измерения:
1 ∘ = 2 π 360 = >>> 




Видео:Радианная мера угла. 9 класс.Скачать

Минуты и секунды [ править | править код ]
По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей [5] ; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).
Минуты и секунды в других системах измерения:
1 ′ = 2 π 360 ∘ ⋅ 60 ′ = 1 ′ p ′ ≈ 1 ′ 3437,747 ′ >cdot 60′>>= 747′>>> 
>> 

>> 
Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.
Угловая секунда [ править | править код ]
Углова́я секу́нда (англ. arcsecond , arc second , as , second of arc ; синонимы: дуговая секунда, секунда дуги [6] ) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла [7] .
Использование [ править | править код ]
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается s ). Соотношение между этими величинами определяется формулой 1 s =15″. [8]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой [6] [9] , что является простой транслитерацией с англ. arcsecond .
Дольные единицы [ править | править код ]
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds , mas ), микросекунды (англ. microarcseconds , µas ) и пикосекунды (англ. picoarcseconds , pas ). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению [7] . Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками [10] , в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами ( mas , µas и pas соответственно).
| Единица | Величина | Обозначение | Аббревиатура | Радиан (прибл.) |
|---|---|---|---|---|
| градус | 1/360 окружности | ° | deg | 17,4532925 mrad |
| минута | 1/60 градуса | ′ | arcmin, amin, ′ ^ >>  , MOA , MOA | 290,8882087 µrad |
| секунда | 1/60 минуты | ″ | arcsec | 4,8481368 µrad |
| миллисекунда | 1/1000 секунды | mas | 4,8481368 nrad | |
| микросекунда | 1 × 10 −6 секунды | μas | 4,8481368 prad |
Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника. [ источник не указан 2692 дня ]
В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP) [11] [12] .
| Главная ≫ Инфотека ≫ Математика ≫ По следам вавилонян, или почему в окружности 360 градусов? // Наталья Карпушина |
| Комментарии: 0 |