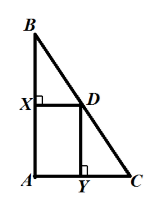4 замечательных точек окружности

Презентация была опубликована 8 лет назад пользователемВиталий Недоплясов

Похожие презентации

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Презентация на тему: » Замечательные точки окружности. I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3.» — Транскрипт:

1 Замечательные точки окружности

2 I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3. Если точка пересечения серединных перпендикуляров сторон треугольника находится вне его, то … 4. Треугольник имеет … медиан. Вариант 2 1. Медианой треугольника называется … 2. Серединным перпендикуляром стороны треугольника называется … 3. Если точка пересечения серединных перпендикуляров сторон треугольника находится на его стороне, то … 4. Треугольник имеет … биссектрис.

3 Новый материал Изобразим треугольник ABC: а) остроугольный; б) прямоугольный; в) тупоугольный. Проведем все его высоты. Сделаем соответствующее предположение и докажем следующую теорему.

4 Теорема. Высоты треугольника или их продолжения пересекаются в одной точке (ортоцентре треугольника).

5 Доказательство. Через вершины данного треугольника АВС проведем прямые, параллельные противоположным сторонам.

7 Заметим, что высоты треугольника могут не пересекаться. Изображен тупоугольный треугольник ABC, в котором продолжения высот AA1, BB1, CC1 пересекаются в одной точке H, а сами высоты не пересекаются. не пересекаются.

8 Задание Изобразим треугольник ABC: а) остроугольный; б) прямоугольный; в) тупоугольный. Проведем все его медианы. Сделаем соответствующее предположение о том, что все медианы треугольника пересекаются в одной точке. Теперь измерим все медианы от вершины до точки пересечения всех медиан, и от этой точки до соответствующей стороны. Сделаем предположение об отношении, в котором делит каждую медиану точка их пересечения и докажем следующую теорему.

9 Теорема. Медианы треугольника пересекаются в одной точке (центроиде треугольника), и делятся в этой точке в отношении 2:1, считая от вершин.

10 Доказательство. В треугольнике АВС проведем медианы АD и ВЕ и их точку пересечения обозначим через О. Отрезок ED будет средней линией треугольника АВС. Проведем среднюю линию HG в треугольнике АВО. Треугольники HGO и EDO равны (по второму признаку равенства треугольников). Следовательно, HO=OE и GO=OD. Таким образом, имеем AG=GO=OD, BH=HO=OE, т.е. медианы АD и BE в точке пересечения делятся в отношении 2:1, считая от соответствующей вершины. Медиана, проведенная из вершины С, также должна делить медиану АD в отно­шении 2:1. Следовательно, она будет проходить через точку О, т.е. все три медианы будут пересекаться в одной точке.

14 VI. Задание на дом 1. Выучить разобранную на уроке теорию (п. 38 учебника). 2. Решить задачи.7,8,11,22,23

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Четыре замечательные точки треугольника

Вы будете перенаправлены на Автор24

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

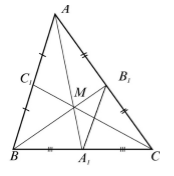
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

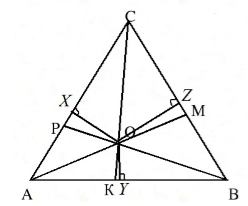
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

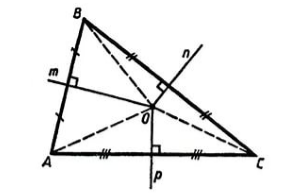
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Видео:Четыре замечательные точки треугольникаСкачать

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

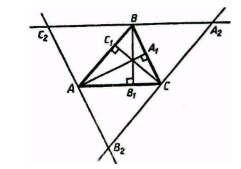
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Видео:Первое условие принадлежности четырех точек одной окружностиСкачать

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2022

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Проект по геометрии «Замечательные точки треугольника»

Сергей Бабенко
Проект по геометрии «Замечательные точки треугольника»

Проект по геометрии на тему «Замечательные точки треугольника»

Содержание

2. Историческая справка

3.1 Элементы треугольника

3.2 Виды треугольников

4. Замечательные точки треугольника, изучаемые в школе

4.1 Точка пересечения высот (ортоцентр)

4.2. Точка пересечения медиан (центроид)

4.3 Точка пересечения биссектрис (инцентр)

4.4 Точка пересечения серединных перпендикуляров (медиатрисс)

4.5 Свойства треугольников (равнобедренный, равносторонний, прямоугольный треугольники)

5. Замечательные точки треугольника, не изучаемые в школе

5.1. Прямая Эйлера

5.2 Изогональные точки

5.3 Окружность Эйлера (окружность девяти точек)

5.4 Точка Жергона

5.5 Точка Нагеля

5.7 Точка Лемуана

5.8 Точка Брокара

5.9 Прямая Симсона

6. Список использованной литературы

Целью данной работы является изучение и обобщение знаний о треугольнике.

1. Введение

Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является как бы символом геометрии. Сегодня школьная геометрия только тогда может стать интересной и содержательной, только тогда может стать собственно геометрией, когда в ней появляется глубокое и всестороннее изучение треугольника.

Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения – никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника.

Значит, изучение школьной геометрии не может осуществляться без глубокого изучения геометрии треугольника; ввиду многообразия треугольника как объекта изучения – а, значит, и источника различных методик его изучения – необходимо подбирать и разрабатывать материал для изучения геометрии замечательных точек треугольника. Причем при подборе этого материала не следует ограничиваться только лишь замечательными точками, предусмотренными в школьной программе Государственным образовательным стандартом, такими как центр вписанной окружности (точка пересечения биссектрис, центр описанной окружности (точка пересечения серединных перпендикуляров, точка пересечения медиан, точка пересечения высот. Но для глубокого проникновения в природу треугольника и постижения его неисчерпаемости необходимо иметь представления как можно о большем числе замечательных точек треугольника. Это совсем не означает, что всем школьникам на уроках геометрии необходимо преподавать материал, например, про точку Ферма или точку Жергонна; но любой школьник должен иметь принципиальную возможность прикоснуться к этому кладезю идей – либо через факультативные занятия, либо самостоятельно.

Помимо неисчерпаемости треугольника как геометрического объекта, необходимо отметить удивительнейшее свойство треугольника как объекта изучения: изучение геометрии треугольника можно начинать с изучения любого его свойства, взяв его за основу; затем методику изучения треугольника можно построить так, чтобы на эту основу нанизывать все остальные свойства треугольника. Другими словами, с чего бы ни начинать изучение треугольника, всегда можно дойти до любых глубин этой удивительной фигуры. Но тогда – как вариант – можно начинать изучение треугольника с изучения его замечательных точек.

В виду вышесказанного, в данном проекте заострим внимание не столько на том, что есть в любых школьных учебниках по геометрии, сколько на том, чего в них нет – это, прежде всего, замечательные точки треугольника, не изучаемые в школе.

Все вышесказанное обосновывает актуальность разработки темы данного проекта.

Целью настоящего проекта является адаптация геометрического материала о замечательных точках треугольника к преподаванию в курсе геометрии 8 класса как в рамках школьной программы, так и на факультативных занятиях.

2. Историческая справка

С одной стороны, история математики – это непрерывный процесс открытий; с другой стороны, открытия в математике, касающиеся геометрии треугольника, были сделаны по преимуществу в Античный период, в период позднего Средневековья и начала Нового времени. Поэтому здесь рассмотрим развитие математики в эти периоды.

Свойства треугольника были хорошо изучены еще в древности греками. В знаменитых «Началах» Евклида доказывается, что центром окружности, описанном около треугольника, является точка пересечения серединных перпендикуляров к его сторонам. Архимед, определяя положение центра тяжести треугольной пластинки, установил, что он лежит на каждой из трех медиан.

Известно, что в «Началах» Евклида излагается материал о центрах вписанной и описанной окружностей, точек пересечения медиан, высот и биссектрис. Есть основания полагать, что греки до Евклида обладали этими знаниями, а Евклид их просто систематизировал и включил в «Начала» для полноты изложения материала.

Принято считать, что вся современная наука оформилась в 17 веке.

Начало открытий замечательных точек треугольника, не изучаемых в школе, положил в 17 веке Джованни Чева (1648 — 1734) – итальянский математик. Основной заслугой Чевы является построение учения о секущих, которое положило начало новой – синтетической геометрии; оно изложено в сочинении «О взаимопересекающихся прямых». Во-первых, его теорема (знаменитая теорема Чевы) сама по себе представляет ценность, во-вторых, ее применение позволило открыть свойства замечательных точек треугольника, известных как точки Нагеля и Жергонна.

Следующим продвижением в истории математики является доказательство Готфридом Лейбницем теоремы о пересечении медиан в 1701 году в Берлине. Воспользовавшись этим результатом, Эйлер в докладе Российской Академии наук изложил факт, известный ныне как свойство прямой Эйлера.

В 19 веке появляется публикация молодого французского математика Ферма расчетов, связанных с минимальным суммарным расстоянием до вершин треугольника.

Уже в конце 19 века Брокар, Нагель и Торричелли, изучая труды Ферма и применяя теорему Чевы, замечают неопубликованные ранее никем некоторые свойства точки Ферма.

Примерно в это же время – вторая половина 19 века – итальянский математик Наполеон Фьеорованти применяет оригинальную идею: по аналогии с «Пифагоровыми штанами», т. е. с построением «равносторонних прямоугольников» на сторонах прямоугольного треугольника, Фьеорованти попробовал построить на сторонах прямоугольного треугольника «равносторонние треугольники». Затем им были сделаны два обобщения этого построения: во-первых, равносторонние треугольники были построены на сторонах произвольного треугольника; во-вторых, была подмечена взаимосвязь внутреннего и внешнего треугольников Наполеона. Таким образом, название «треугольники Наполеона» этому построению было дано по аналогии с построениями Пифагора, и к императору Наполеону Бонапарту эти треугольники никакого отношения не имеют.

3. Треугольник

3.1 Элементы треугольника

Треугольник – многоугольник с тремя сторонами, или замкнутая ломаная линия с тремя звеньями, или фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой.

Основные элементы треугольника ABC

Вершины – точки А; В и С

Стороны – отрезки АВ; ВС и АС, соединяющие вершины;

Углы – Углы часто обозначают так же, как и вершины, – буквами A, B и C.

3.2 Виды треугольников

Существует две классификации треугольников: по углам и сторонам.

Классификация по углам

Определение. Треугольник называется остроугольным, если все три его угла — острые.

Определение. Треугольник называется тупоугольным, если один из его

углов -тупой, то есть больше 90 градусов.

Определение. Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90 градусов. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.

Классификация по сторонам

Определение. Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

Определение. Треугольник, у которого все стороны равны, называется равносторонним или правильным.

4. Замечательные точки треугольника, изучаемые в школе.

Поясним сначала смысл выражения «замечательные точки треугольника». Всем известно, что биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанной в этот треугольник окружности. Также в одной точке пересекаются медианы и высоты треугольника, серединные перпендикуляры к его сторонам. Все точки, получающиеся в результате пересечения перечисленных наборов из трех прямых, назовем замечательными – замечательное в них, прежде всего то, что три различные прямые на плоскости, как правило, пересекаются в трех различных точках, а не в одной.

Приведем некоторый теоретический материал школьного курса геометрии по замечательным точкам треугольника.

Каждый треугольник имеет три медианы, три биссектрисы и три высоты, причем каждая тройка прямых пересекается в одной точке. Эти точки, вообще говоря, отличны друг от друга, однако для правильного треугольника совпадают с его центром.

4.1 Точка пересечения высот (ортоцентр)

Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.

Основное свойство высот. Три высоты в треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника. В остроугольном треугольнике ортоцентр лежит внутри треугольника, в прямоугольном — совпадает с вершиной прямого угла, а в тупоугольном треугольнике — находится вне треугольника на пересечении продолжений высот.

4.2 Точка пересечения медиан (центроид)

Медианой треугольника называют отрезок, соединяющий его вершину с серединой противолежащей стороны.

Основное свойство медиан: в любом треугольнике медианы пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершины.

Точка пересечения медиан треугольника имеет простой физический смысл: она является его центром масс. Представим, что треугольник нарисован на жесткой, но практически невесомой пластине и в его вершинах укреплены три тяжелых шарика одинаковой массы. Из физики известно, что в плоскости треугольника найдется такая точка М, что если подвесить за нее пластинку с шариками, то вся система будет пребывать в равновесии, то есть, как бы ее ни расположить, она будет оставаться неподвижной в том положении, в котором мы ее отпустим. Мы будем обозначать эту точку буквой М. Ее также называют центроидом или центром масс треугольника. Отметим несколько свойств медианы:

Медиана разбивает треугольник на два равновеликих, то есть имеющих одинаковую площадь.

Три медианы разбивают треугольник на шесть равновеликих.

Отрезки, соединяющие точку пересечения медиан с вершинами треугольника, разбивают треугольник на три равновеликие части.

4.3 Точка пересечения биссектрис (инцентр)

Биссектрисой треугольника называют отрезок прямой, делящей угол при вершине на две равные части.

Основное свойство биссектрис: точка пересечения – центр вписанной окружности.

Биссектриса внутреннего угла треугольника есть геометрическое место точек, равноудаленных от сторон этого угла. Две биссектрисы обязательно пересекутся в одной точке.

Эта точка будет равноудалена от сторон угла А и от сторон угла В и, следовательно, от сторон угла С. Это означает, что точка лежит также и на третьей биссектрисе и равноудалена от всех трех сторон треугольника – то есть является центром вписанной в него окружности. Эту точку называют инцентром.

Биссектрисы внутренних углов треугольника пересекаются в центре вписанной окружности.

Свойство биссектрисы внутреннего угла треугольника: биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные заключающим ее сторонам.

Любой треугольник имеет единственную описанную окружность, центр которой лежит на пересечении серединных перпендикуляров к его сторонам.

4.4 Точка пересечения серединных перпендикуляров (медиатрисс)

Серединный перпендикуляр к стороне треугольника есть геометрическое место точек, равноудаленных от ее концов. Серединные перпендикуляры к двум сторонам обязательно пересекаются в одной точке.

Эта точка будет равноудалена от концов каждой из двух сторон, т. е. от всех вершин треугольника. Это и означает, что она является центром описанной около треугольника окружности. Ясно также, что она лежит и на третьем серединном перпендикуляре, т. е. все три перпендикуляра пересекаются в одной точке.

4.5 Свойства треугольников

Равнобедренный треугольник

Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой.

Также равны биссектрисы, медианы и высоты, проведённые из этих углов.

Биссектриса, медиана и высота, проведенные к основанию, совпадают между собой.

Центры вписанной и описанной окружностей лежат на этой линии.

Углы, противолежащие равным сторонам, всегда острые (следует из их равенства).

Равносторонний треугольник

Каждая из высот является одновременно биссектрисой и медианой.

Центры описанной и вписанной окружностей совпадают.

5. Замечательные точки треугольника, не изучаемые в школе

5.1 Прямая Эйлера

Во всяком треугольнике точка пересечения медиан, точка пересечения высот (или их продолжений) и точка пересечения серединных перпендикуляров к сторонам треугольника лежат на одной прямой (эта прямая называется прямой Эйлера)

5.2 Изогональные точки

Прямые, симметричные высотам относительно соответствующих биссектрис, проходят через центр описанной окружности, то есть содержат ее радиусы.

Справедливо также следующее: если три прямые, проведенные из вершин треугольника, пересекаются в одной точке, то и прямые, симметричные им относительно соответствующих биссектрис, тоже проходят через одну и ту же точку.

Подобные две точки называются изогональными. Таким образом, ортоцентр треугольника (синяя точка) изогонален центру описанной окружности.

5.3 Окружность девяти точек

Середины сторон треугольника, основания его высот и середины отрезков от вершин до ортоцентра лежат на одной окружности

Ее радиус равен половине радиуса описанной окружности, а центр лежит посередине отрезка, где N — центр описанной окружности, а точка

S — ортоцентр треугольника. Такая окружность называется окружностью девяти точек, или окружностью Эйлера, или окружностью Фейербаха — по имени Карла Фейербаха, провинциального учителя математики из Германии, родного брата философа Людвига Фейербаха.

5.4 Точка Жергонна

Три отрезка, соединяющие вершины треугольника с точками, в которых вписанная в него окружность касается соответственно противоположных вершинам сторон, пересекаются в одной точке J. Она называется точкой Жергонна

5.5 Точка Нагеля

Отрезки, соединяющие каждую из вершин треугольника с точкой, в которой противоположная сторона касается соответствующей вневписанной окружности, пересекаются в одной точке N – точке Нагеля. Она интересна тем, что отрезок NI, где I – центр вписанной окружности, проходит через центр тяжести M (точка пересечения медиан) треугольника и делится им в отношении NM:MI = 2:1

5.6 Точка Ферма

Построим на сторонах произвольного треугольника АВС, вне его, равносторонние треугольники ABC’, BCA’, CAB’. Тогда шесть кривых — три окружности, описанные вокруг этих правильных треугольников, и прямые AA’, BB’, CC’ пересекаются в одной точке X. Если все углы треугольника ABC не превосходят 120 градусов, то X лежит в треугольнике ABC и является точкой Ферма S. В этом случае углы между отрезками AS, BS и CS равны между собой и, значит, равны 120 градусов. Более того, длины отрезков AA’, BB’ и CC’, называемых линиями Симпсона, тоже равны между собой и равны AS + BS + CS. Если один из углов треугольника ABC больше 120 градусов, то X лежит вне треугольника ABC, а точка Ферма S совпадает с вершиной тупого угла. Точка S — точка Ферма, то есть точка, сумма расстояний от которой до всех вершин треугольника ABC минимальна.

5.7 Точка Лемуана

Отразив относительно биссектрис треугольника соответствующие медианы, получаем новые замечательные линии — симедианы.

Точка L их пересечения называется точкой Лемуана треугольника. Она является центроидом треугольника KMN, образованного ее проекциями на стороны исходного треугольника.

5.8 Точка Брокара

Если на сторонах треугольника АВС внешним образом построить подобные ему треугольники СА1В, САВ1 и С1АВ (углы при первых вершинах всех четырех треугольников равны и т. д., то прямые АА1, ВВ1 и СС1 пересекутся в точке Р, которую называют точкой Брокара. Одна из особенностей этой точки состоит в том, что угол РАС = углу РСВ = углу РВА.

5.9 Прямая Симсона

Основания перпендикуляров, опущенных из точки P описанной окружности треугольника на его стороны или их продолжения, лежат на одной прямой – прямой Симсона.

Верно и обратное утверждение: если основания перпендикуляров, опущенных из некоторой точки Р на стороны треугольника или их продолжения, лежат на одной прямой, то точка P лежит на описанной окружности треугольника.

Заключение

В разработке проекта приведена историческая справка об открытиях в области замечательных точек треугольника – выбрана самая краткая и существенная информация касательно истории развития геометрии замечательных точек треугольника;

Изложен геометрический материал по замечательным точкам треугольника, как изучаемым, так и не изучаемым в школьном курсе геометрии.

Дан ряд задач с решениями, многие проиллюстрированы чертежами.

Задачи включающие в себя решение и разбор тем по замечательным точкам треугольника в школьной программе раскрываются не полностью и большая часть остается неизученной. Такие задачи для учеников являются сложными и непривычными, в течение изучения данной темы по школьной программе не вырабатываются необходимые навыки по решению таких задач. Данная тема может частично раскрыться лишь на внеклассных занятиях или с помощью самостоятельного обучения.

Результатом проекта является мультимедийный продукт (презентация).

6. Список использованной литературы

1. Атанасян Л. С. Геометрия: Учеб. для общеобразовательных. учреждений. – М. : Просвещение, 2008.

2. Большая математическая энциклопедия / Якушева Г. М. и др. – М. : Филол. О-во «СЛОВО»: ОЛМА-ПРЕСС, 2005. – 639 с. : ил.

3. Возникновение и развитие математической науки: Кн. Для учителя. – М. : Просвещение, 1987. – 159 с. : ил.

4. За страницами учебника алгебры: Кн. для учащихся 7 – 9 кл. сред. Шк. — М. : Просвещение, 1990. – 224 с. : ил.

5. Панов В. Ф. Математика древняя и юная/ Под ред. В. С. Зарубина. – 2-е изд., испр. – М. : Изд-во МГТУ им. Н. Э. Баумана, 2006. – 648с.

6. Энциклопедия для детей. Т. 11. Математика / Глав. ред, М. Д. Аксёнова. – М. : Аванта+,1998. – 688 с. : ил.

7. Энциклопедия. Мудрость тысячелетий. – М. : ОЛМА-ПРЕСС, 2004. –

🎬 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

Коллаб 4 каналов. 4 замечательные точки трапецииСкачать

Условие принадлежности четырёх точек одной окружностиСкачать

четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать

Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

ЕГЭ Задание 16 Условие принадлежности четырех точек окружностиСкачать

Геометрия 8 класс. Четыре замечательные точки треугольникаСкачать

1 2 4 сопряжение окружностейСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Точки на числовой окружностиСкачать

Геометрия 8 класс : Решение задач. 4 замечательные точкиСкачать

Четыре замечательные точки треугольника. Видеоурок 20. Геометрия 8 классСкачать