Если прямые AB и AC пересекают окружность S3 соответственно в точках M и N (отличных от B и C), то равнобедренные треугольники AO1C и NO3C имеют равные углы при вершине C. Поэтому их углы при вершинах A и N также равны. Следовательно, O3N || O1A. Аналогично O3M || O2A.
- Три окружности с центрами O1, O2 и O3
- Три окружности, радиусы которых равны 2, 3, 4 соответственно, попарно касаются внешним образом в точках A, B, C?
- Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, касаются сторон угла с вершиной A?
- Углы B и C треугольника ABC равны соответственно 73 и 77?
- Ребята, помогите, пожалуйста?
- 895 баллов?
- Углы b и c треугольника abc равны соответственно 13 и 17 найдите BC если радиус окружности описанной около треугольника ABC равен 6?
- Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А?
- Две касающиеся внешним образом в точке К окружности, радиус одной из которых в двое больше радиуса другой, вписаны в угол c вершиной A?
- 1. Около окружности, радиус которой равен 12, описан правильный шестиугольник?
- Около треугольника АВС с равными сторонами АВ и ВС описана окружность радиуса R?
- Три окружности , имеющие радиусы 1, 2 и 3 попарно касаются друг друга внешним образом?
- 🔥 Видео
Видео:Интересная задача о трёх попарно касающихся окружностяхСкачать

Три окружности с центрами O1, O2 и O3
Три окружности с центрами O1, O2 и O3 радиусами 1, 2 и 6 соответственно попарно касаются внешним образом. Найдите угол O1O2O3.
Решение: 
O1O2=3
O2O3=8
O1O3=7
По теореме косинусов:
O1O3 2 =O1O3 2 +O2O3 2 -2O1O2∙O2O3∙cos(O1O2O3)
7 2 =8 2 +3 2 -2∙8∙3∙cos(O1O2O3)
49=64+9-48∙cos(O1O2O3)
48∙cos(O1O2O3)=64+9-49
48∙cos(O1O2O3)=24
cos(O1O2O3)=0,5
∟O1O2O3=60°
Видео урока, где рассмотрено решение этой задачи и не только.
Кликните СЮДА, чтобы посмотреть видео.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Видео:Как найти стороны равнобокой трапеции, описанной около трёх попарно касающихся равных окружностей?Скачать
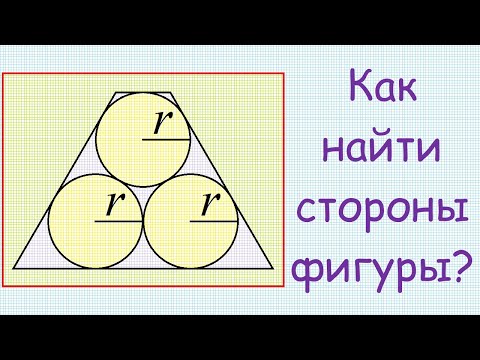
Три окружности, радиусы которых равны 2, 3, 4 соответственно, попарно касаются внешним образом в точках A, B, C?
Геометрия | 5 — 9 классы
Три окружности, радиусы которых равны 2, 3, 4 соответственно, попарно касаются внешним образом в точках A, B, C.
Найдите радиус окружности, описанной около треугольника ABC.
Пусть О1, О2 и О3 — центры данных нам окружностей, точки А, В и С — точки их касания.
Тогда О1А = О1С = 2, О2А = О2В = 3, О3В = О3С = 4.
Значит стороны треугольника О1О2О3 равны : 5, 6 и 7.
Тогда площадь этого треугольника по Герону равна :
S = √[p * (p — a)(p — b)(p — c)], где р — полупериметр, а, b, с — стороны треугольника.
Р = (5 + 6 + 7) / 2 = 9.
S = √(9 * 4 * 3 * 2) = 6√6.
Заметим, что окружность, описанная вокруг треугольника АВС — это вписанная в треугольник О1О2О3 окружность, так как точки А, В и С окружности принадлежат сторонам О1О2, О2О3 и О3О1 соответственно.
Есть формула нахождения длины отрезка от вершины треугольника до точки касания с вписанной окружностью : расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно d = (a + b — c) / 2 или d = р — с, где р — полупериметр, с — сторона, противоположная углу треугольника.
В нашем случае : О1А = 9 — 7 = 2, О2А = 9 — 6 = 3, О3В = 9 — 5 = 4, следовательно, точки касания вписанной в треугольник АВС окружности совпадают с точками А, В и С касания данных нам окружностей.
Радиус вписанной в треугольник окружности равен r = S / p или в нашем случае
r = 6√6 / 9 = 2√6 / 3.
Ответ : r = 2√6 / 3.
Видео:Геометрия Три равные окружности радиуса r попарно касаются одна другой. Вычислить площадь фигурыСкачать

Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, касаются сторон угла с вершиной A?
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, касаются сторон угла с вершиной A.
Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C.
Найдите радиус окружности, описанной около треугольника ABC.
Видео:Геометрия Три окружности разных радиусов попарно касаются друг друга. Отрезки, соединяющие их центрыСкачать

Углы B и C треугольника ABC равны соответственно 73 и 77?
Углы B и C треугольника ABC равны соответственно 73 и 77.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 9.
Видео:Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Ребята, помогите, пожалуйста?
Ребята, помогите, пожалуйста!
))) Две касающиеся внешним образом в точке К окружности, радиусы которых равны 22 и 33, касаются сторон угла с вершиной А.
Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С.
Найдите радиус окружности, описанной около треугольника АВС.
Видео:Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать

895 баллов?
Нужна помощь бакалавров.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, вписаны в угол с вершиной A.
Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C.
Найдите радиус окружности, описанной около треугольника ABC.
Видео:Три окружности касаются прямой и друг друга внешним образомСкачать
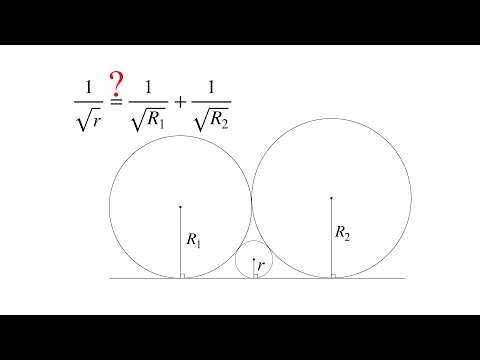
Углы b и c треугольника abc равны соответственно 13 и 17 найдите BC если радиус окружности описанной около треугольника ABC равен 6?
Углы b и c треугольника abc равны соответственно 13 и 17 найдите BC если радиус окружности описанной около треугольника ABC равен 6.
Видео:Геометрия Три окружности радиусов R1 = 6 см, R2 = 7 см, R3 = 8 см попарно касаются друг другаСкачать

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А?
Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А.
Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С, Найдите радиус окружности, описанной около треугольника АВС.
Видео:ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

Две касающиеся внешним образом в точке К окружности, радиус одной из которых в двое больше радиуса другой, вписаны в угол c вершиной A?
Две касающиеся внешним образом в точке К окружности, радиус одной из которых в двое больше радиуса другой, вписаны в угол c вершиной A.
Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C.
Найти радиус окружности, описанной около треугольника ABC, если AB = корень из 3.
Пожалуйста, с чертежом!
Видео:КРАСИВАЯ ПЛАНИМЕТРИЧЕСКАЯ ЗАДАЧА (3 ОКРУЖНОСТИ)Скачать

1. Около окружности, радиус которой равен 12, описан правильный шестиугольник?
1. Около окружности, радиус которой равен 12, описан правильный шестиугольник.
Найдите радиус окружности, описанной около этого шестиугольника.
2 Найдите радиус окружности, вписанной в правильный шестиугольник со стороной 54.
3. Найдите радиус окружности, описанной около квадрата со стороной, равной 12.
4. Сторона правильного треугольника равна 4.
Найдите радиус окружности, вписанной в этот треугольник.
5. Радиус окружности, описанной около правильного треугольника, равен 18.
Найдите высоту этого треугольника.
6. Около окружности , радиус которой равен 16, описан квадрат.
Найдите радиус окружности, описанной около этого квадрата.
Видео:Геометрия Две окружности с центрами O1 и O3 и радиусами 4,5 и 2,5 касаются друг с другом внешнимСкачать

Около треугольника АВС с равными сторонами АВ и ВС описана окружность радиуса R?
Около треугольника АВС с равными сторонами АВ и ВС описана окружность радиуса R.
Угол С треугольника равен а (острый).
Точка Е — середина дуги ВС описанной окружности.
Найти радиус окружности, касающейся внешним образом описанной окружности в точке Е и прямой АВ.
Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Три окружности , имеющие радиусы 1, 2 и 3 попарно касаются друг друга внешним образом?
Три окружности , имеющие радиусы 1, 2 и 3 попарно касаются друг друга внешним образом.
Найдите радиус окружности, проходящей через центры данных окружностей.
Вы открыли страницу вопроса Три окружности, радиусы которых равны 2, 3, 4 соответственно, попарно касаются внешним образом в точках A, B, C?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
5 : 4 : 2, соответственно стороны будут равны 15 : 12 : 6 см, а периметр 33 см.
AC = 1, 55 мм правильна відповідь.
Вот, держи ответ) очень легко.
Вот, держи решение. Надеюсь, помогла : ).
Тот у которого все стороны равны ( конгруэнтны) как у и квадрата. У ромба это такое свойство и его нельзя до казать только на рисуя.
1 случай когда т N лежит между точками М и К MK = MN + NK = 7 + 5 = 12дм 2 случай когда т К лежит между точками M и N MK = MN — NK = 7 — 5 = 2 дм.
Длина дуги C = πR * α / 180 C = 36, α = 45 Меньшая дуга ограничивает сектор в 45гр, значит большая в 360 — 15 = 315гр, т. Е. в 315 : 45 = 7 раз больше. См = πR * 45 / 180 Сб = πR * 7 * 45 / 180 Тогда длина длина большей дуги равна 36 * 7 = 252.
Решение : 1)Внешний угол∠AOB равен : 2) Составим и решим задачу с помощью пропорции. Получаем : ⇒найдем x через выражение ⇒ 3) . .
Есть треугольник АВС и серединные перпендикуляры k и m к сторонам АВ и ВС. Назовем точку пересечения прямых k и m — точка О. По свойству серединного перпендикуляра для прямой k : ОА = ОВ, а для прямой m : ОВ = ОС. Но тогда ОА = ОС. Т. е. Точка О..
🔥 Видео
Г: Три равные окружности с центрами О1, О2, О3 и радиусом R попарно касаются друг друга в точках А ВСкачать

ЕГЭ Задание 16 Три окружностиСкачать
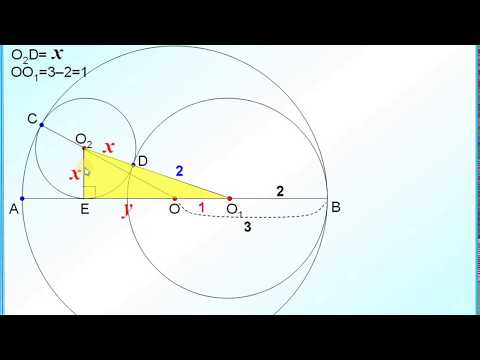
ЕГЭ Задание 16 Внешнее касание трёх окружностейСкачать
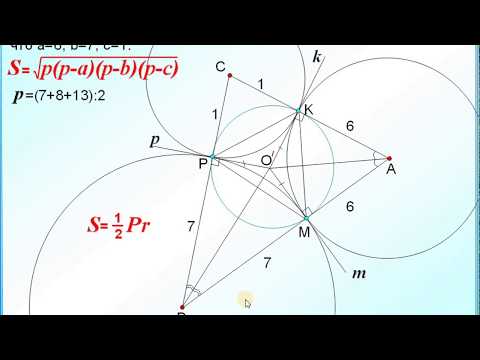
Геометрия Две окружности радиусом R = 3 см и r = 1 см касаются внешним образом. Найти расстояние отСкачать

С4, егэ. Задача про три касающиеся друг друга окружностиСкачать

10 класс, 11 урок, Числовая окружностьСкачать

ЗАДАЧА ПРО 3 ОКРУЖНОСТИ ЗА 3 МИНУТЫ - №25 ОГЭ | Математика для каждого | Дмитрий КостенкоСкачать

Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать











