240 градусов на окружности по часовой стрелке

Видео:УГОЛ МЕЖДУ СТРЕЛКАМИ ЧАСОВСкачать

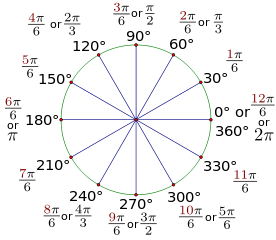
Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:Формулы приведения - как их легко выучить!Скачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Видео:Определение угла между часовой и минутной стрелкойСкачать

Школе NET

Register

Do you already have an account? Login

Login

Don’t you have an account yet? Register

Newsletter

Submit to our newsletter to receive exclusive stories delivered to you inbox!

Суррикат Мими

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Найдите заданные точки на числовой окружности:
4пи/3 , пи/6 , 240 градусов, 180 градусов

Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Лучший ответ:

Таня Масян

Начнём с последнего вопроса

4/3*π = 4/3*180 = 60*4 = 240° — ответ

Сама полярная шкала на рисунке в приложении.

Для её построения потребуется циркуль и транспортир (чертёжные угольники в 45° и 30°/60°

Видео:Задача нашего времени Когда минутная стрелка догонит часовуюСкачать

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac =frac =frac .) Тогда радианная мера угла: $$ angle AOB=frac =frac =frac $$

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например:

Отметим на числовой окружности точки, соответствующие (frac , frac , frac , frac , pi), а также (-frac , -frac , -frac , -frac , -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac , frac , frac ), и (-frac ). Все четыре точки совпадают, т.к. begin Mleft(frac right)=Mleft(frac +2pi kright)\ frac -2pi=-frac \ frac +2pi=frac \ frac +4pi=frac end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac lt t lt frac $$ а также, с учетом периода $$ -frac +2pi klt tltfrac +2pi k $$
Интервал
$$ -frac leq t leq frac $$ а также, с учетом периода $$ -frac +2pi kleq tleqfrac +2pi k $$
Полуинтервал
$$ -frac leq t ltfrac $$ а также, с учетом периода $$ -frac +2pi kleq tltfrac +2pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^ =frac .\ EC=60^ =frac .\ AE=EC+CD=90^ +30^ =120^ =frac .\ ED=EC+CD=60^ +90^ =150^ =frac . end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; frac ; frac ; frac ).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac =-90^ , frac =135^ \ frac =210^ , frac =315^ end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; 5pi; frac ; frac ).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac =frac cdotpi=-6pi+frac rightarrow frac =90^ \ 5pi=4pi+pirightarrow pi=180^ \ frac =frac pi=3pi-frac rightarrow pi-frac =frac \ frac =frac pi=7pi-frac rightarrow pi-frac =frac end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac =1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac approx frac =4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb )), запишите количество полученных базовых точек.

$$ frac $$	$$ -frac +2pi k $$
Четыре базовых точки, через каждые 90°	Две базовых точки, через каждые 180°
$$ frac +frac $$	$$ -frac $$
Три базовых точки, через каждые 120°	Пять базовых точек, через каждые 72°

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

Видео:ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Видео:Тригонометрическая окружностьСкачать

Измерение углов

Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.

На картинке видны 4 разных угла, образованных пересечением прямых AB и CD

Обычно углы измеряются в градусах, что обозначается как °. Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°). Таким образом, градус — это $frac$ круга.

Видео:5. Как найти точки на тригонометрической окружности. Отрицательные углы в градусах и радианах.Скачать

Углы больше 360 градусов

Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.

Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.

Пример 2
1. Найти количество кругов, описанных объектом, образующем угол
a) 380°
b) 770°
c) 1000°
Решение
a) 380 = (1 × 360) + 20
Объект описал один круг и 20°
Так как $20^ = frac = frac$ круга
Объект описал $1frac$ кругов.

b) 2 × 360 = 720
770 = (2 × 360) + 50
Объект описал два круга и 50°
$50^ = frac = frac$ круга
Объект описал $2frac$ круга
c)2 × 360 = 720
1000 = (2 × 360) + 280
$280^ = frac = frac$ кругов
Объект описал $2frac$ кругов

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Положительные и отрицательные углы

Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.

В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.

Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)

Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360. Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.

Пример 3
1. Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°

2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°

2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°

Видео:Как искать точки на тригонометрической окружности.Скачать

Радиан

Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга. Это единица измерения угловой величины. Такой угол примерно равен 57,3°.
В большинстве случаев, это обозначается как рад.
Таким образом $1 рад approx 57,3^$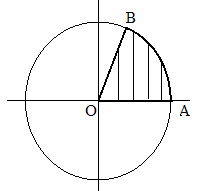

Радиус = r = OA = OB = AB
Угол BOA равен одному радиану

Поскольку длина окружности задается как $2pi r$, то в окружности $2pi$ радиусов, а значит в целом круге $2pi$ радиан.

Радианы обычно выражаются через $pi$ во избежание десятичных частей в вычислениях. В большинстве книг, аббревиатура рад (rad) не встречается, но читатель должен знать, что, когда речь идет об угле, то он задан через $pi$, а единицами измерения автоматически становятся радианы.

Пример 4
1. Преобразовать 240°, 45°, 270°, 750° и 390° в радианы через $pi$.
Решение
Умножим углы на $frac$.

2. Преобразовать следующие углы в градусы.
a) $fracpi$
b) $3,12pi$
c) 2,4 радиан
Решение
$180^ = pi$
a) $frac pi = frac times 180 = 225^$
b) $3,12pi = 3,12 times 180 = 561,6^$
c) 1 рад = 57,3°
$2,4 = frac = 137,52$

Отрицаетльные углы и углы больше, чем $2pi$ радиан

Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2pi$.

Пример 5
1. Преобразовать $-fracpi$ и $-fracpi$ в позитивные углы в радианах.

Решение
Прибавляем к углу $2pi$
$-fracpi = -fracpi + 2pi = fracpi = 1fracpi$

Когда объект вращается на угол больший, чем $2pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2pi$, результат равен или меньше, но как можно ближе к данному числу.

Пример 6
1. Найти количество кругов пройденных объектом при данных углах
a) $-10pi$
b) $9pi$
c) $fracpi$

Решение
a) $-10pi = 5(-2pi)$;
$-2pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.

b) $9pi = 4(2pi) + pi$, $pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки

c) $fracpi=3,5pi=2pi+1,5pi$, $1,5pi$ равно три четверти цикла $(frac=frac)$
объект прошел один и три четверти цикла против часовой стрелки

📸 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

3. Как найти точки на тригонометрической окружности. Положительные углы в градусах.Скачать

12 часов Тригонометрии с 0.Скачать

Тригонометрия. Урок 3. Решение упражнений. Единичная числовая окружность.Скачать

Что такое радиан?Скачать

Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Вычисление значений тригонометрических функций на координатном кругеСкачать