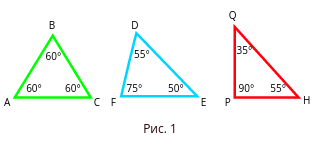180 градусов в треугольнике правило (8 видео)

Сумма углов треугольника

Сумма углов треугольника — это сумма
всех внутренних углов треугольника.

Так, как углы измеряются в градусах, соответственно значение
суммы углов треугольника также измеряется в градусах.

Сумма углов треугольника есть величина постоянная,
неизменяемая, она равна 180 градусам, вне зависимости
от вида рассматриваемого треугольника.

На рисунке 1 изображены равносторонний,
разносторонний и прямоугольный треугольники,
их суммы внутренних углов равны 180 градусам.

Также, существует теорема, которая доказывает
утверждение о том, что сумма углов треугольника
180 градусов, она называется теоремой
о сумме углов треугольника.

Теорема о сумме углов треугольника — это теорема в
геометрии о сумме углов произвольного треугольника на плоскости.

Содержание

Сумма углов треугольника — чему она равна?
Теорема — чему равны сложенные между собой углы произвольного треугольника?
Что следует из геометрической теоремы
Теорема о сумме углов треугольника
Формулировка теоремы о сумме углов треугольника
Доказательство теоремы
Следствие из теоремы
Классификация треугольников по видам углов
Пояснение на примерах
📺 Видео

Видео:ПОЧЕМУ СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180? #shorts #геометрия #егэ #огэ #треугольникСкачать

Сумма углов треугольника — чему она равна?

Сумма углов треугольника — важная, но достаточно простая тема, которую проходят в 7 классе на геометрии. Тема состоит из теоремы, короткого доказательства и нескольких логичных следствий. Знание этой темы помогает в решении геометрических задач при последующем изучении предмета.

Видео:Сумма углов треугольника равна 180Скачать

Теорема — чему равны сложенные между собой углы произвольного треугольника?

Теорема гласит — если взять любой треугольник вне зависимости от его вида, сумма всех углов неизменно составит 180 градусов. Доказывается это следующим образом:

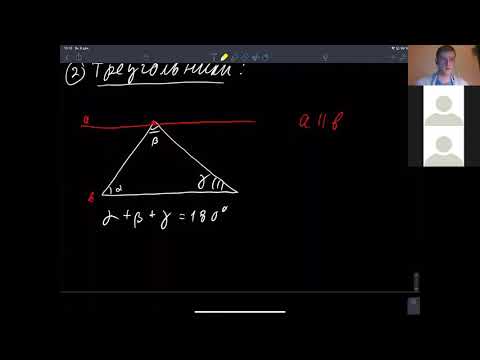
для примера берут треугольник АВС, через расположенную на вершине точку В проводят прямую линию и обозначают ее, как «а», прямая «а» при этом строго параллельна стороне АС;
между прямой «а» и сторонами АВ и ВС обозначают углы, маркируя их цифрами 1 и 2;
угол 1 признают равным углу А, а угол 2 — равным углу С, поскольку эти углы считаются накрест лежащими;
таким образом, сумма между углами 1, 2 и 3 (который обозначается на месте угла В) признается равной развернутому углу с вершиной В — и составляет 180 градусов.

Если сумма углов, обозначенных цифрами, составляет 180 градусов, то и сумма углов А, В и С признается равной 180 градусам. Это правило верно для любого треугольника.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Что следует из геометрической теоремы

Принято выделять несколько следствий из приведенной теоремы.

Если в задаче рассматривается треугольник с прямым углом, то один из его углов будет по умолчанию равен 90 градусам, а сумма острых углов также составит 90 градусов.
Если речь идет о прямоугольном равнобедренном треугольнике, то его острые углы, в сумме составляющие 90 градусов, по отдельности будут равны 45 градусам.
Равносторонний треугольник состоит из трех равных углов, соответственно, каждый из них будет равен 60 градусам, а в сумме они составят 180 градусов.
Внешний угол любого треугольника будет равняться сумме между двумя внутренними углами, не прилегающими к нему.

Можно вывести следующее правило — в любом из треугольников есть как минимум два острых угла. В некоторых случаях треугольник состоит из трех острых углов, а если их только два, то третий угол будет тупым либо прямым.

Также нужно знать, что предусмотрены специальные названия для сторон прямоугольных треугольников. «Длинная» сторона, которая расположена напротив прямого угла, называется гипотенузой, а оставшиеся «короткие» стороны носят название катетов. В последующих темах геометрии эти названия упоминаются очень часто.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Теорема о сумме углов треугольника

Видео:Сумма углов треугольникаСкачать

Формулировка теоремы о сумме углов треугольника

Треугольник может иметь различные углы — острые, прямой, тупой, — но сумма их величин не может превышать 180 градусов. Эта закономерность отражена в теореме, доказательство которой имеет несколько вариантов.

Сумма углов в треугольнике всегда равна 180 о .

Данная теорема является одной из основных, рассматриваемых на уроках геометрии.

Рассмотрим рисунок с треугольником ABC:

Треугольник имеет углы: A, B, C. Это углы внутренние. Складывая их величины, неизменно получаем 180о. При этом не имеет значения, данный треугольник равнобедренный, равносторонний или прямоугольный.

Исходя из такого свойства, треугольник не может иметь два тупых угла, поскольку их сумма будет более 180о.

Смысл теоремы о сумме углов треугольника был известен еще в Древнем Египте, его установили эмпирическим путем, т.е. путем наблюдения. Однако вероятно, что в то время отсутствовало доказательство этого утверждения. Его можно обнаружить в трудах Прокла, когда он давал комментарии к «началам» Евклида.

В книге № 1 евклидовских «Начал» приведено иное доказательство данной теоремы, чем принято сейчас. Оно опирается на соответствующий чертеж.

Рассматриваемая теорем приписывается не только Евклиду, но и Пифагору. Она много раз подвергалась сомнению в неевклидовой геометрии.

Видео:Почему сумма углов в треугольнике 180 градусов? #умскул #егэпрофиль #математикаегэ #математикаСкачать

Доказательство теоремы

Продолжим рассмотрение треугольника ABC из предыдущего раздела.

Для доказательства теоремы проведем дополнительную прямую линию так, чтобы она была параллельна стороне AC и проходила через вершину треугольника B (угол 2).

Таким образом, в районе угла B образовалось три угла (№№ 4, 2, 5). Из рисунка видно, что их сумма равняется 180о.

На данном рисунке имеются накрест лежащие углы: №1 и №4. Их образование произошло при пересечении прямой AB двух параллельных прямых AC и α. Углы №3 и №5 — также накрест лежащие. Только образованы они при пересечении прямой BC двух параллельных прямых AC и α.

Углы №1 и №4, а также №3 и №5 попарно равны.

Поскольку сумма углов №№ 4, 2, 5 равна 180о, а углы №4 можно заменить №1, а №5 — №3, сумма углов №№ 1, 2, 3 также равна 180о.

Такое доказательство опирается на свойства углов, образованных при пересечении двух параллельных прямых третьей.

Видео:Почему сумма углов треугольника 180 градусов?Скачать

Следствие из теоремы

Формулировка теоремы о сумме углов треугольника имеет несколько следствий. Среди них:

Если в треугольнике один из углов прямой, то сумма прочих двух углов равна 90о. Свойство вытекает из обычного алгебраического действия. Обозначим углы прямоугольного треугольника A, B, C. Допустим, что C=90о. Тогда (A+B)=180о+90о.
Для равнобедренного прямоугольного треугольника характерно, что каждый из его острых углов равен 45о.
Треугольник, у которого равны длины всех трех сторон, имеет равные углы — 60о.
Углы любого треугольника либо все являются острыми, либо острых два, а третий равен 90о либо больше 90о (тупой).
Сумма двух внутренних углов, которые не смежны с внешним, равна величине этого внешнего угла.

Видео:Почему сумма углов в треугольнике равна 180 градусовСкачать

Классификация треугольников по видам углов

Рассматривая треугольники, как многоугольники с тремя вершинами, в геометрии выделяют их следующие разновидности:

Остроугольный треугольник (все три вершины представляют собой острые углы).
Прямоугольный (одна из вершин составляет 90о). Стороны, которые образуют данный угол, — катеты, а сторона, противолежащая углу в 90о, — гипотенуза.
Тупоугольный (одна из вершин представлена тупым углом, а две другие — острыми).

В зависимости от особых характеристик сторон треугольника, существует еще одна классификация:

Треугольник с тремя равными сторонам — равносторонний.
Треугольник с двумя равными сторонами — равнобедренный.

Приведенная классификация подразумевает существование определенных признаков у каждой из названных групп. Эти признаки приходят на помощь в решении задач, когда нужно доказать особенности каких-либо геометрических фигур. Так:

Больший угол всегда расположен напротив большей стороны.
Равные углы всегда расположены так, что напротив них — равные стороны.
Любой треугольник (равносторонний, равнобедренный, тупоугольный, прямоугольный и т. п.) имеет 2 острых угла.
Любой внешний угол всегда по размеру превышает внутренний и равен сумме прочих, не смежных с ним, углов.

Для прямоугольного треугольника существуют еще несколько свойств, вытекающих из его определения и изложенных в учебниках по геометрии:

Напротив катетов всегда расположены острые углы.
Гипотенуза всегда превышает по своей длине любой из катетов, однако меньше их суммы.
Тот катет, напротив которого находится острый угол величиной 30о, равен половине длины гипотенузы.
Сумма квадратов катетов равна квадрату гипотенузы. Данное свойство доказывается теоремой Пифагора.

Примечание 2

Существуют отдельные свойства для равнобедренного треугольника. Его высота, проведенная в направлении основания, совпадает с медианой и биссектрисой того угла, который расположен между равными сторонами. Кроме того, она совпадает с осью симметрии треугольника, проведенной по основанию.

Видео:Сумма внутренних углов треугольника равна 180 градусовСкачать

Пояснение на примерах

Рассмотрим особенности треугольников, приведенные выше, на примерах.

Сколько градусов составляет один из углов треугольника, если величины других 25о и 42о?

Исходя из теоремы о сумме углов в треугольнике, производим следующие вычисление:

Следовательно, данный треугольник тупоугольный.

Известно, что в треугольнике один из углов равен сумме двух других. К какому виду треугольников относится данная геометрическая фигура?

Обозначим угол, равный сумме двух других углов, за X. Тогда X+2X/2=180 Путем математических действий приходим к уравнению следующего вида: 2X=180, откуда X=90о.

Ответ: данный треугольник имеет прямой угол, поэтому является прямоугольным.

Дан треугольник ABC. В нем угол C на 15о больше, чем угол A, а угол B — на 30о его меньше. Найти величину каждого из углов.

Обозначим X величину угла A. Тогда угол C=X+15, B=X-30

Используем свойство суммы углов треугольника и составляем уравнение:

Ответ: угол A=65о, угол B=65-30=35о, угол C=65+15=80о.

Для проверки можно сложить величины полученных результатов: 65+35+80=180о. Следовательно, задача решена верно.

Про треугольник ABC известно, что угол A составляет 60о, угол B — 80о. Из угла A на сторону BC опущена биссектриса, образовав треугольник ACD. Каких величин углы имеет данный треугольник?

Исходя из определения биссектрисы, мы знаем, что это луч, который начинаясь в вершине угла треугольника и деля его на два равных угла, пересекает противоположную сторону в определенной точке.

Поскольку биссектриса делит угол A пополам, образованный угол DAB равен 30о, а угол ADC=30+80=110о (поскольку это внешний угол треугольника).

Исходя из правила, что сумма углов в треугольнике равна 180о, проводим математическое действие:

Ответ: Угол C равен 40о.

В треугольнике ABC известна величина одного угла: A = 40о. Известно, что также что угол, смежный с углом B, составляет 70о. Определить величины всех углов.

Решение задания заключается в уравнении. Обозначим величину угла C за X. Тогда

Данный вариант решения основан на том свойстве, что если сумма смежных углов равна 180о (а именно это мы видим на рисунке относительно угла B), то величина каждого из них равна 180о минус величина смежного угла.

Ответ: Величина угла C = 30о, угла B — 110о.

Проверочным действием является операция сложения всех известных и найденных величин углов: 110о+30о+40о=180о.

В треугольнике ABC известен угол A (40о). Кроме того, по условию этот треугольник равносторонний (AC=BC). Найти величины двух оставшихся углов.

Известно утверждение, что в равностороннем треугольнике величины углов прилегающих к этим сторонам, равны. Следовательно, углы B и A равны. Используя теорему о сумме углов в треугольнике, принимая величину угла C за X, составляем равенство:

Ответ: Величина угла B равна 40о, угла C — 100о. Следовательно, треугольник является тупоугольным.