15 какой треугольник называется равносторонним

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:Виды треугольниковСкачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Что такое равносторонний треугольник

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Определение равностороннего треугольника

Равносторонним треугольником называется такой треугольник $ABC$, у которого все стороны равны: $AB = BC = AC$.

Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Свойства равностороннего треугольника

В равностороннем треугольнике все углы равны.

Любая биссектриса, равностороннего треугольника равна его медиане и высоте. Если сторона равностороннего треугольника равна $a$, то

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Примеры решения задач

Задание. Определить, чему равны углы в равностороннем треугольнике.

Решение. По свойству равностороннего треугольника, в нем все углы равны. Обозначим эту величину через $x$, то есть $alpha=beta=gamma=x$. Так как сумма всех углов треугольника равна $180^$, справедливо равенство

Ответ. В равностороннем треугольнике все углы по $60^$

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Виды треугольников

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.

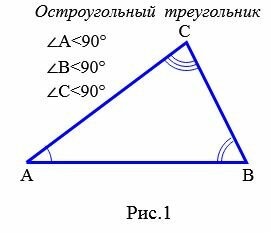
Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).

Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).

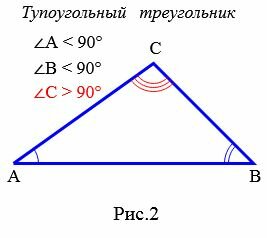Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).

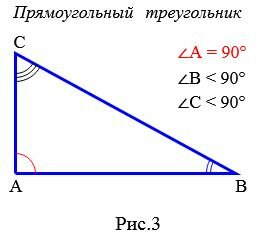Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).

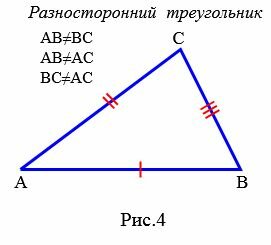Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).

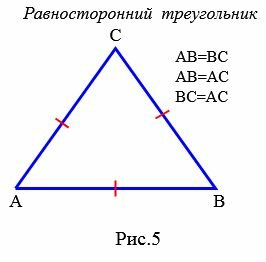Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).

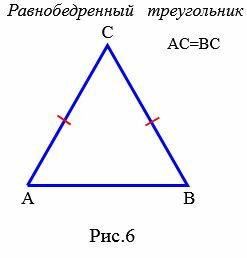В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.

🎦 Видео

Виды треугольников 3 классСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Равносторонний треугольник в окружностиСкачать

Формулы равностороннего треугольника #shortsСкачать

Виды треугольниковСкачать

Треугольники №15. Средняя линия. Средняя линия трапеции №17. Равносторонний треугольник. (ОГЭ)Скачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

7 фактов про равносторонний треугольникСкачать