15 градусов угла треугольника

Как найти значения тригонометрических функций для угла 15 градусов

Найдем значения синуса, косинуса и тангенса для угла 15 градусов аналитическим способом.
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 15 градусов — задача сложная. Однако, это не совсем так.
Нам на помощь придут формулы преобразования двойного угла тригонометрических функций.

Дело в том, что мы можем представить угол в 30 градусов, как двойной угол 15 градусов ( 2 * 15 ).

Тогда, отталкиваясь от тождества:
cos 2α = 1 — 2sin 2 α

Принимаем двойной угол как 2 * 15 градусов, тогда
cos 30 = 1 — 2sin 2 15
sin 2 15 = ( 1 — cos 30 ) / 2

Значение косинуса для угла 30 градусов легко вычислить. Оно равно √3/2
sin 2 15 = ( 1 — √3/2 ) / 2
sin 15 = √ (( 1 — √3/2 ) / 2 )
верхнюю часть дроби под корнем приведем к общему знаменателю (2)
sin 15 = √ (( (2 — √3) /2 ) / 2 ) = √( (2 — √3) / 4 )
теперь у нас одна дробь под знаком корня. Умножим числитель и знаменатель на два
sin 15 = √( (2 — √3) / 4 ) = √( (4 — 2√3) / 8 )
самый интересный момент, мы можем представить 4 — 2√3 как (√3-1) 2
тогда
sin 15 = √( (√3-1) 2 / 8 ) = (√3-1)/ √8 = (√3-1)/ (2√2)

путем несложных агебраических преобразований получаем:

Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 15 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств преобразований двойных углов и половин заданных углов.

См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).

Ниже приведены также значения тригонометрических функций для угла 15 градусов в виде десятичной дроби с четырьмя знаками после запятой.

Видео:Головоломка №12. Найти гипотенузу. Угол 15 градусов. 7-кл.Скачать

Углы прямоугольного треугольника

Смотрите также

Спасибо, за онлайн-расчёт. Углы для спусков на ножах рассчитываю. Класс!

Что б я делал без этой услуги?! Рассчитал стропила за минуту!

Считаю крышу, очень удобный сервис !
Спасибо !

Спасибо! Пригодилось для нахождения угла конуса (на работе)

Единственный сайт где углы отображены графически, все остальные (особо одаренные) не додумались. Благодарю!

Спасибо большое, а то школьные знания с годами выветрились)))

Спасибо. Быстро, вовремя, без загвоздка.

Отличная программа, очень помогло

Спасибо, сайт очень выручил. Делали перила для лестницы)))

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Как найти стороны прямоугольного треугольника

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

🌟 Видео

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Измерение угла с помощью транспортираСкачать

Как найти площадь треугольника с углом 15 градусовСкачать

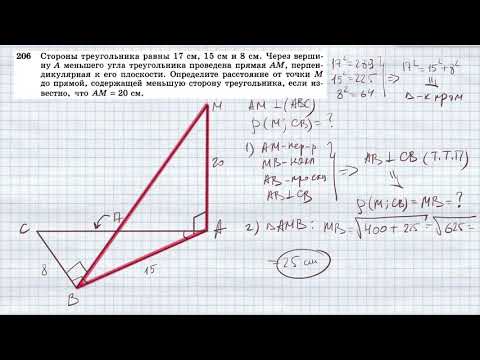
№206. Стороны треугольника равны 17 см, 15 см и 8 см. Через вершину A меньшего угла треугольника проСкачать

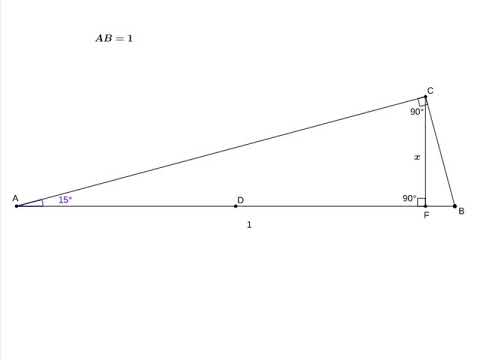
Прямоугольный треугольник с углом в 15 градусов № 8Скачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

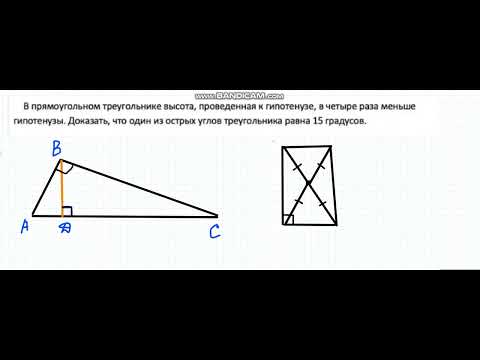
№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

Построение углов заданной градусной мерыСкачать

Прямоугольный треугольник и угол в 15 градусовСкачать

Олимпиада 8 класс. Найти площадь прямоугольного треугольника с углом в 15 градусов и гипотенузой 8.Скачать

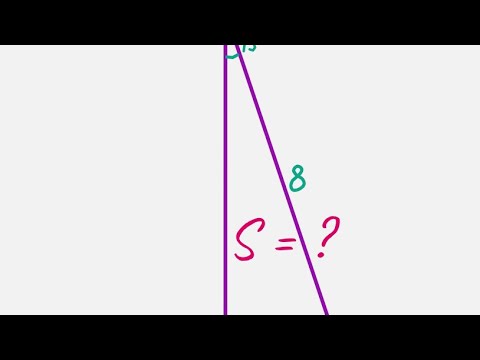
КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Классный способ для разметки любого угла без транспортира.Скачать

Сумма углов треугольника. Видеоурок 15. Геометрия 7 класс.Скачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать