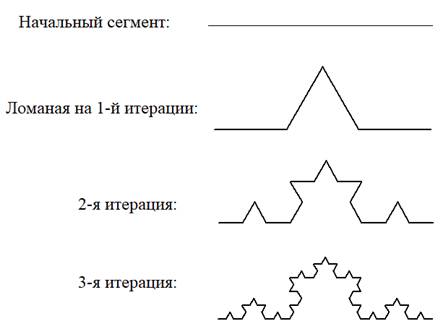
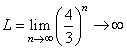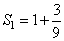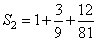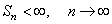Звезда коха из треугольников (8 видео) | Курс школьной геометрии

Кривая Коха и снежинка Коха

Я решил начать знакомство с фракталами с простого классического примера – кривой Коха. Строится она по простому правилу: каждый ее линейный сегмент на последующей итерации заменяется ломаной:

Начинать можно с прямой линии. Затем, на 1-й итерации она заменяется ломаной, состоящей из 4-х линейных сегментов равной длины. Причем, длина этой ломаной в точности равна длине линейного сегмента. То есть, углы между прямыми составляют 60 градусов. На 2-й итерации каждый линейный сегмент заменяется точно такой же ломаной, только уменьшенной в три раза. И так далее. В результате, у нас получается самоподобная кривая, которая получила название кривой Коха в честь автора – шведского математика Хельге фон Коха:

В то время еще не было понятия фракталов и это был лишь пример кривой, которая всюду непрерывна, но нигде не дифференцируема. Математик Шарль Эрмит окрестил их «монстрами», а общее научное мнение полагало, что это пример некой математической «патологии» интересной, скорее, исследователям, чем настоящим ученым. Знали бы они тогда, что именно такие кривые лягут в основу описания многих реальных природных процессов и форм. Новые революционные идеи часто в истории встречали такое неприятие.

Но вернемся к кривой Коха. Это пример фрактальной формы. По каким признакам сделан такой вывод? Во-первых, это самоподобие. Здесь отчетливо видно, что на большем масштабе кривая будет оставаться визуально неизменной. Но одного самоподобия мало. Например, известная картина «Черный квадрат» Малевича тоже обладает самоподобием. Этот квадрат можно составить из четырех квадратов меньшей размерности:

Однако, гений Малевича все же не создал фрактала. Что еще не хватает для получения фрактальной формы? Дробной размерности! Квадрат принадлежит плоскости, имеет целую размерность 2, а кривая Коха – находится в дробной размерности, примерно, 1,2618. Я пока опущу вопрос как она была вычислена, мы к этому еще вернемся, главное, что фракталы должны принадлежать дробной размерности. Получаем два важных условия, которыми обладают фрактальные формы:

1) должна быть самоподобной;

2) должна принадлежать дробной размерности.

Обратите внимание, это не определение фракталов. Сам термин (фрактал) все еще находится в развитии и пока полностью не определен. Но эти два условия, на мой взгляд, должны выполняться.

Итак, что же придает фракталам дробная размерность и почему она так важна? Давайте еще наз взглянем на кривую Коха.

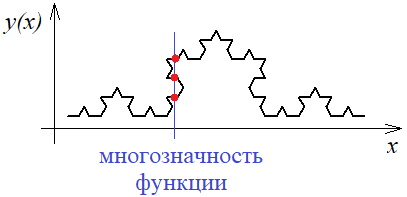
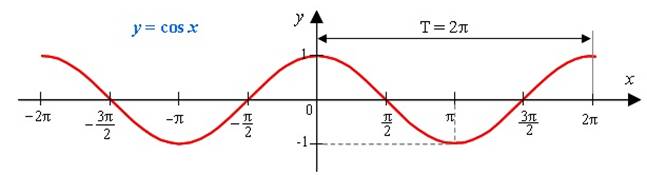
Если ее представить в координатных осях, то получим, что одному значению x соответствует несколько значений y. Такие кривые уже не являются одномерными, когда одному значению x соответствует только одно значение y, например, функция cos(x) одномерна:

И в то же время, множество точек кривой Коха по вертикали не выстраиваются в непрерывную линии, а значит, не покрывают все двумерное пространство. Отсюда и получается дробная размерность между единицей и двойкой. Благодаря этой дробности, множество точек кривой Коха образуют узор, а не просто заполняют двумерное пространство, как это было в случае «Черного квадрата» Малевича. Поэтому дробность размерности – характерная черта, наверное, всех фракталов.

Интересной особенностью кривой Коха является ее длина: она постоянно увеличивается по мере увеличения итераций. Действительно, вначале отрезок условно можно принять за 1. Затем, на 1-й итерации он заменяется ломаной, длина которой равна 4/3. На 2-й итерации каждый линейный сегмент заменяется уменьшенной ломаной длиной (4/3)/3 = 4/6 и таких сегментов ровно 4, то есть, суммарная длина линии, равна 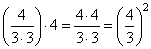. 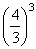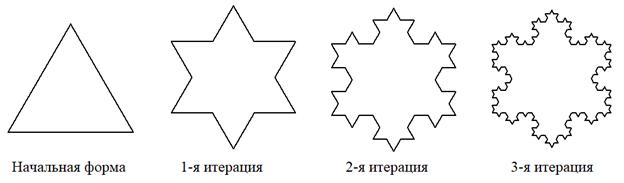На следующей итерации длина станет , и так далее. Получается, что при числе итераций, стремящихся к бесконечности, длина:

А что с площадью фрактальных фигур? Она тоже будет увеличиваться до бесконечности? Давайте посмотрим. Для этого сделаем построение уже не кривой Коха, а снежинки Коха. Здесь все делается аналогично, только начальная форма является равносторонним треугольником, а не линией:

Если начальную площадь равностороннего треугольника принять за единицу, то на первой итерации площадь увеличится на три малых треугольника, площади которых в 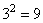раз меньше площади исходного треугольника. То есть, площадь составит:

На 2-й итерации имеем дополнительно 12 еще меньших треугольников с площадями в 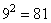раз меньших, исходной площади:

И так далее, то есть, слагаемые в сумме стремительно уменьшаются при увеличении номера итерации и в пределе:

По-моему, неплохой способ предложить своим знакомым нарисовать фигуру с бесконечным периметром, но конечной площадью. У большинства задачка вызовет недоумение – как такое возможно? В школьной программе такого пока не проходят.

Итак, мы с вами познакомились с принципами формирования кривой Коха и снежинки Коха. Узнали о двух необходимых условиях, формирующих фрактальные формы: самоподобие и дробность размерности. И образно попытались уловить восприятие дробного пространства. Если эти моменты вам понятны, то цель этого занятия достигнута.

Содержание

Звезда коха из треугольников
Исследовательские работы и проекты
Звезда Кох
1.2. Звезда Кох
Построение звезды Кох
Длина кривой, ограничивающей звезду Кох
Площадь звезды Кох
Звезда Кох из квадратов
Снежинка Коха
Основные свойства кривой Коха
Варианты
🔍 Видео

Видео:Что Такое Фракталы? Простое Объяснение!Скачать

Звезда коха из треугольников

Видео:#1. Кривая Коха и снежинка Коха | Фракталы на PythonСкачать

Исследовательские работы и проекты

Видео:Снежинка КохаСкачать

Звезда Кох

Видео:Снежинка из треугольника Фрактал КохаСкачать

1.2. Звезда Кох

Один из первых примеров автоподобных фигур был придуман немецким математиком Хельгой фон Кох. Называется звезда Кох.

Построение звезды Кох

Для её построения к начальному равностороннему треугольнику последовательно добавляют новые, подобные ему, треугольники.

На первом шаге стороны правильного треугольника разбиваются на три равные части и их середины заменяются на правильные треугольники, подобные исходному. В результате получается правильный звездчатый шестиугольник. Стороны этого шестиугольника снова разбиваются на три равные части, а их середины заменяются на правильные треугольники.

Длина кривой, ограничивающей звезду Кох

Мы можем выяснить, какова длина кривой, ограничивающей звезду Кох.

Предположим, что сторона исходного равностороннего треугольника равна 1, и периметр равен 3. На следующем шаге количество сторон увеличивается в 4 раза, а длина каждой из них в 3 раза меньше исходной.

Периметр правильного звездчатого шестиугольника будет равен (3*4)/3=4. На каждом следующем шаге периметр многоугольника будет увеличиваться в 4/3 раза.

Из этого следует, что кривая Кох, к которой приближаются многоугольники, имеет бесконечную длину.

Площадь звезды Кох

Вычислим площадь звезды Кох.

Пусть площадь исходного равностороннего треугольника равна 1. На первом шаге добавляем 3 равносторонних треугольника, со сторонами в 3 раза меньшими исходных.

Площадь каждого такого треугольника равна 1/9. Следовательно, площадь правильного звездчатого шестиугольника равна 1+3/9=4/3.

На следующем шаге добавляется 12 треугольников суммарной площади 12/81. Поскольку длины сторон треугольников на каждом шаге уменьшаются в 3 раза, их площадь уменьшается в 9 раз. Число добавляемых треугольников равно числу сторон многоугольника и на каждом шагу увеличивается в 4 раза.

Поэтому площадь звезды Кох представляет собой площадь исходного треугольника плюс сумма геометрической прогрессии с начальным членом 3/9 и знаменателем 4/9.

Звезда Кох из квадратов

Еще один вариант звезды Кох можно построить из квадратов последовательным прибавлением к исходному квадрату подобных ему квадратов.

На первом шаге стороны квадрата разбиваются на 3 равные части и их середины заменяются на квадраты, подобные исходному. Стороны получившегося многоугольника снова разбиваются на 3 равные части и их середины заменяются на квадраты.

Повторяя этот процесс, будем получать всё более сложные многоугольники, всё более приближающиеся к искомой фигуре.

Видео:Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуляСкачать

Снежинка Коха

Для просмотра анимации необходимо включить JavaScript.

Эта фигура — один из первых исследованных учеными фракталов. Она получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Линии с таким свойством были известны и раньше (Карл Вейерштрасс построил свой пример еще в 1872 году), но кривая Коха замечательна простотой своей конструкции. Не случайно его статья называется «О непрерывной кривой без касательных, которая возникает из элементарной геометрии».

Рисунок и анимация отлично показывают, как по шагам строится кривая Коха. Первая итерация — просто начальный отрезок. Потом он делится на три равные части, центральная достраивается до правильного треугольника и затем выкидывается. Получается вторая итерация — ломаная линия, состоящая из четырех отрезков. К каждому из них применяется такая же операция, и получается четвертый шаг построения. Продолжая в том же духе, можно получать всё новые и новые линии (все они будут ломаными). А то, что получится в пределе (это уже будет воображаемый объект), и называется кривой Коха.

Основные свойства кривой Коха

1. Она непрерывна, но нигде не дифференцируема. Грубо говоря, именно для этого она и была придумана — как пример такого рода математических «уродцев».

2. Имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3) n –1 . Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.

3. Снежинка Коха ограничивает конечную площадь. И это при том, что ее периметр бесконечен. Это свойство может показаться парадоксальным, но оно очевидно — снежинка полностью помещается в круг, поэтому ее площадь заведомо ограничена. Площадь можно посчитать, и для этого даже не нужно особых знаний — формулы площади треугольника и суммы геометрической прогрессии проходят в школе. Для интересующихся вычисление приведено ниже мелким шрифтом.

Пусть сторона исходного правильного треугольника равна a. Тогда его площадь . Сначала сторона равна 1, а площадь: . Что происходит при увеличении итерации? Можно считать, что к уже имеющемуся многоугольнику пристраиваются маленькие равносторонние треугольнички. В первый раз их всего 3, а каждый следующий раз их в 4 раза больше чем было в предыдущий. То есть на n-м шаге будет достроено T_n = 3 · 4 n –1 треугольничков. Длина стороны каждого из них составляет треть от стороны треугольника, достроенного на предыдущем шаге. Значит, она равна (1/3) n . Площади пропорциональны квадратам сторон, поэтому площадь каждого треугольничка равна . При больших значениях n это, кстати, очень мало. Суммарный вклад этих треугольничков в площадь снежинки равен T_n · S_n = 3/4 · (4/9) n · S₀. Поэтому после n-го шага площадь фигуры будет равна сумме S₀ + T₁ · S₁ + T₂ · S₂ + . +T_n · S_n = . Снежинка получается после бесконечного числа шагов, что соответствует n → ∞. Получается бесконечная сумма, но это сумма убывающей геометрической прогрессии, для нее есть формула: . Площадь снежинки равна .

4. Фрактальная размерность равна log4/log3 = log₃4 ≈ 1,261859. . Аккуратное вычисление потребует немалых усилий и подробных разъяснений, поэтому здесь приведена, скорее, иллюстрация определения фрактальной размерности. Из формулы степенной зависимости N(δ)

(1/δ) D , где N — число пересекающихся квадратиков, δ — их размер, а D — размерность, получаем, что D = log_1/_δN. Это равенство верно с точностью до прибавления константы (одной и той же для всех δ). На рисунках изображена пятая итерация построения кривой Коха, зеленым закрашены квадратики сетки, которые с ней пересекаются. Длина исходного отрезка равна 1, поэтому на верхнем рисунке длина стороны квадратиков равна 1/9. Закрашено 12 квадратиков, log₉12 ≈ 1,130929. . Пока не очень похоже на 1,261859. . Смотрим дальше. На среднем рисунке квадратики в два раза меньше, их размеры 1/18, закрашено 30. log₁₈30 ≈ 1,176733. . Уже лучше. Внизу квадратики еще вдвое меньше, закрашено уже 72 штуки. log₇₂30 ≈ 1,193426. . Еще ближе. Дальше нужно увеличивать номер итерации и одновременно уменьшать квадратики, тогда «эмпирическое» значение размерности кривой Коха будет неуклонно приближаться к log₃4, а в пределе и вовсе совпадет.