Найти расстояние между двумя точками на окружности (8 видео)

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Содержание

Числовая ось
Прямоугольная декартова система координат на плоскости
Формула для расстояния между двумя точками координатной плоскости
Уравнение окружности на координатной плоскости
Окружность
Что такое окружность?
Как найти длину окружности
Формулы:
Чему равен радиус окружности
Окружность в тригонометрии
Что еще важно знать?
Углы поворота
Расстояния между двумя точками
Расстояния между двумя точками
Вывод формулы для вычисления расстояния между двумя точками на плоскости
🔍 Видео

Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:Длина отрезкаСкачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Формула для расстояния между двумя точками координатной плоскости

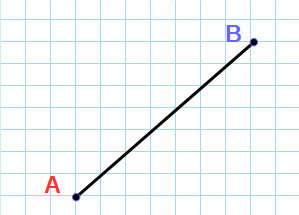
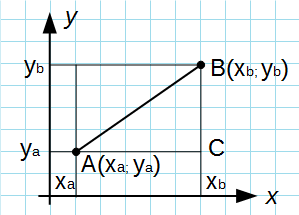
Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Видео:Расстояние между точками по координатам.Скачать

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать

Окружность

Привет, друг! Ниже собрана вся информация по окружности: что это такое, как найти ее величины, как круг связан с тригонометрией. Это поможет тебе еще лучше разобраться с этими темами, а также верно решать задачи! Время прочтения — 10 минут.

Видео:Уравнение окружности (1)Скачать

Что такое окружность?

Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки, а ее радиусом называют отрезок, который соединяет любую её точку с центром (все радиусы окружности равны). У окружности также есть диаметр — отрезок, соединяющий две точки окружности и проходящий через её центр.

Выделяют также такое понятие как единичная окружность. Она представляет из себя такую окружность, центр которой располагается в начале координат, а ее радиус равен единице.

Есть еще один вид окружности — числовая. Это обычная единичная окружность, но с уже установленным соответствием между действительными числами и точками.

Видео:Расстояние между точкамиСкачать

Как найти длину окружности

Зачастую в задачах просят найти длину окружности, как это сделать?

Так, для того чтобы найти длину окружности, нужно:

Диаметр этой окружности умножить на , число ≈ 3,1415926535…

Найти удвоенное произведение радиуса и числа

Видео:Расстояние между двумя точками с заданными координатамиСкачать

Формулы:

Где r — это радиус окружности, а d — ее диаметр, а число — это математическая константа (отношение длины окружности к длине ее диаметра)

Чему равен радиус окружности

Радиус окружности необходимо знать, чтобы решить многие задачи, поэтому давай вместе разберем, как его можно найти.

Через площадь окружности : R=s, где S — площадь круга, — это математическая константа, которая объяснена выше.
Через длину круга: R=P2, где P — длина круга.
Через диаметр окружности: R=d2, где d — диаметр.
Через диагональ вписанного треугольника: R=d2, где d=a2 b2.
Через сторону описанного квадрата: R= a2, где а — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника: R=abc4S, где abc — стороны вписанного треугольника, а S — его площадь.
Через площадь и полупериметр описанного треугольника: R=sp, где S — площадь треугольника, а p — полупериметр.
Через площадь сектора и его центральный угол: R=360Spa, где S — площадь сектора круга, α — его центральный угол.
Через сторону вписанного правильного многоугольника: R=a2sin(180N), где a — сторона правильного многоугольника (все его стороны равны), N — количество сторон многоугольника.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Окружность в тригонометрии

Окружность используется и в тригонометрии:

Что значат на рисунке все обозначение?

Присутствует перевод градусов в радианы (и наоборот). В полном круге — 360 градусов ( радиан);

Значение косинуса угла — на оси Х, а значение синуса — на У;

Синус и косинус имеют значения от -1 до 1;

На тригонометрическом круге видно, что косинус как и синус — периодические (один период равен 2).

Видео:Евклидово расстояние на пальцах. Как определить расстояние между двумя точками.Скачать

Что еще важно знать?

Полный круг — 360 градусов.

Точка с координатами (1;0) — угол 0 градусов соответствует углу ноль градусов, а точка с координатами (-1;0) соответствует углу 180 градусов, точка с координатами (0;1) — в 90 градусов.

Косинус угла — абсцисса точки на единичной окружности, которая соответствует приведенному углу.

Синус угла — ордината точки на единичной окружности, которая соответствует приведенному углу.

Потому как окружность единичная, то для любого угла и синус, и косинус находятся в пределах от -1 до 1. Так:

Из этого можно выделить основное тригонометрическое тождество:

cos^2 a + sin^2 a = 1

По рисунку видно, что

Углы могут быть и больше 360 градусов. Например, угол 720 — это два полных оборота по часовой стрелке. Из этого можно сделать такой вывод:

Если же применять в этих формулах не градусы, а радианы, то:

Можно также по рисунку тригонометрической окружности определить тангенс угла и котангенс:

В результате, мы получаем таблицу:

Видео:Расстояние между двумя точкамиСкачать

Углы поворота

Угол поворота — это угол, образованный положительным направлением оси OX и лучом OA.

Их величина не имеет зависимости от радиуса приведенной окружности.

Угол в первом квадранте(четверти круга), имеет все положительные значения тригонометрических функций.

Во втором квадранте все функции (кроме sin и cos) — отрицательные.

В третьем квадранте значения всех функций (помимо tg и ctg) меньше 0.

В четвертом квадранте все функции (кроме cos и sec) с отрицательным значением.

Видео:#1 Поиск расстояния между двумя точкамиСкачать

Расстояния между двумя точками

На данной странице калькулятор поможет рассчитать расстояние между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.

Расстояние между двумя точками — это длина отрезка, которая соединяет эти точки.

Расстояния между двумя точками

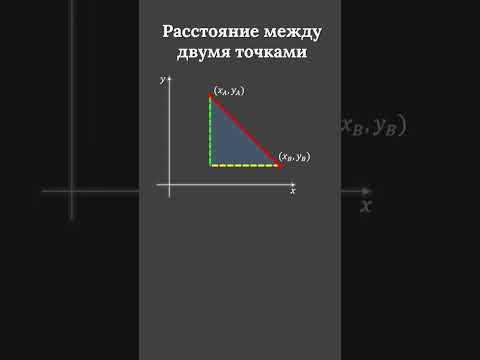
Формула вычисления расстояния между двумя точками A(x_a; y_a) и B(x_b; y_b) на плоскости:

Формула вычисления расстояния между двумя точками A(x_a; y_a; z_a) и B(x_b; y_b; z_b) в пространстве:

Вывод формулы для вычисления расстояния между двумя точками на плоскости

Из точек A и B опустим перпендикуляры на оси координат x и y.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

Спомощью теоремы Пифагора, вычислим длину отрезка AB:

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.