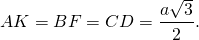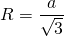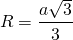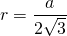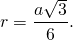Замечательная точка в равностороннем треугольнике (6 видео)

Свойства равностороннего треугольника

Основные свойства равностороннего треугольника непосредственно следуют из свойств равнобедренного треугольника, частным случаем которого он является.

Свойства равностороннего треугольника

2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:

AK — высота, медиана и биссектриса, проведённые к стороне BC;

BF — высота, медиана и биссектриса, проведённые к стороне AC;

CD — высота, медиана и биссектриса, проведённые к стороне AB.

Длины всех трёх высот (медиан, биссектрис) равны между собой:

Если a — сторона треугольника, то

3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).

4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:

5) Расстояние от точки пересечения высот, биссектрис и медиан

до любой вершины треугольника равно радиусу описанной окружности:

6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности:

7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.

8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности:

Содержание

Свойства равностороннего треугольника: теория и пример задачи
Определение равностороннего треугольника
Свойства равностороннего треугольника
Свойство 1
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Свойство 6
Пример задачи
Ззамечательные точки треугольника — свойства, применение и примеры решения
Точка пересечения медиан треугольника
Точка пересечения биссектрис треугольника
Точка пересечения высот треугольника
Пример решения задач с построением
🔍 Видео

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

R – радиус описанной окружности;
r – радиус вписанной окружности;
R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Видео:Равнобедренный треугольник. 7 класс.Скачать

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Ззамечательные точки треугольника — свойства, применение и примеры решения

Замечательные точки треугольника не просто так описываются таким прилагательным. Для многих учеников, а начинают знакомиться с этим понятием в 8 классе, эта тема кажется наиболее интересной и простой в курсе геометрии, поэтому многочисленные теоремы и свойства запоминаются достаточно просто.

Итак, какие же четыре точки называются замечательными? Перечислим их:

точку пересечения медиан треугольника;

точку пересечения биссектрис треугольника;

точку пересечения высот треугольника;

точку пересечения серединных перпендикуляров сторон треугольника.

Все точки обладают своими особенностями и свойствами, про всех есть свои теоремы и следствия из них. Кроме того, существует свойство, которое справедливо сразу для четырёх этих точек. Вне зависимости от того, медиана ли это, биссектриса или высота, все они пересекаются в одной точке.

Замечательные точки характерны не только для треугольников. Например, в трапеции так же четыре замечательные точки.

Теперь рассмотрим основные положения, связанные с замечательными точками треугольника.

Видео:Формулы равностороннего треугольника #shortsСкачать

Точка пересечения медиан треугольника

Из курса геометрии известно определение медианы треугольника.

На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС.

Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан.

Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С.

На отрезке АВ отметьте центр С1, на стороне ВС центр А1, на АС центр В1.

Проведите 3 медианы из вершин. Из угла А – медиана АА1,из угла В — медиана ВВ1, из угла С — медиана СС1.

Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством).

Изучим следующее свойство точки пересечения трёх медиан треугольника.

Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка:

A1G = 2AG, B1G = 2BG, C1G = 2CG.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Точка пересечения биссектрис треугольника

Прежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её.

Рассмотрим пример. Дано:

угол ВАС Точка пересечения серединных перпендикуляров сторон треугольника

Для начала вспомним определение серединного перпендикуляра. Теорема о серединном перпендикуляре:

Сделаем краткое доказательство. Соединим концы отрезка с вершиной серединного отрезка. Докажем равенство полученных треугольников, из чего следует АD = DB.

Построим эту точку.

В треугольнике АВС отмечаем середины его сторон. Проводим три серединных перпендикуляра КО, LO, МО и отмечаем точку их пересечения О.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Точка пересечения высот треугольника

Проведём три высоты в ∆АВС, все они пересекутся в т. Н. Точка Н по отношению к ∆АВС – ортоцентр.

Свойство высот треугольника:

если все три высоты треугольника или их продолжения пересекаются в одной точке, то это ортоцентр;

СH * HНС
= АH * АНА = ВH * ВНВ.

Ортоцентр может располагаться внутри треугольника, снаружи или совпадать с одной из вершин.

На рисунке показано расположение ортоцентра в остроугольном, прямоугольном и тупоугольном треугольниках.

Видео:Геометрия Равносторонний треугольникСкачать

Пример решения задач с построением

Замечательные точки треугольника замечательные именно потому, что они имеют много полезных для решения задач свойств. Рассмотрим пример решения задачи на эту тему.

Серединный перпендикуляр в ∆АВС, опущенный к АС, пересекает ВС в т. В. Найти BD, DC, если AD = 5 см BC = 9 см.

Сделаем дополнительное построение – серединный отрезок КD к прямой АС. Тогда DK это и высота, и медиана в ∆АВС. Если в треугольнике проведена прямая, которая является высотой и медианой, то он равнобедренный. Значит, AD = DC = 5 см.

ВD =ВС — DC = 4 см.

Ответ: DC = 5 см, ВD = 4 см.