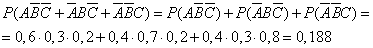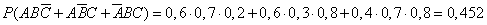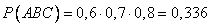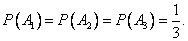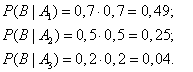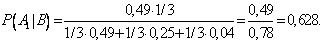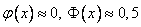Закон прямоугольного треугольника теория вероятностей

Прямоугольное (равномерное) распределение — простейший тип непрерывных распределений. Если случайная переменная X может принимать любое действительное значение в интервале (а, b), где а и b – действительные числа, и если каждому значению случайной переменной соответствует одинаковая плотность вероятности, то переменная X имеет прямоугольное распределение. Иногда пользуются термином «равномерное распределение».

Из приведенного определения следует, что плотность распределения вероятностей этой случайной переменной должна быть постоянной, т. е. что в интервале (a, b) f(x) = с. Отсюда, а также из условия, что интеграл от функции f(x), взятый в интервале (а, b), должен равняться единице, нетрудно найти функцию плотности вероятности f(x). Имеем:

(4.1)

откуда cb – са = 1 и, следовательно, получим . Таким образом, функция плотности вероятности для прямоугольного распределения:

для a ≤ x ≥ b. (4.2)

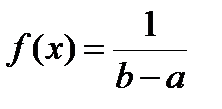
Для х > b и х 2 (X) равняется:

(4.5)

Прямоугольное распределение находит широкое применение в математической статистике. Оно имеет основополагающее значение для так называемых непараметрических методов – одного из новейших разделов статистики, находящего все более широкое применение. Понятием прямоугольного распределения иногда пользуются и в теории статистических оценок – в том разделе статистики, где изучаются методы построения выводов о значениях параметров в генеральной совокупности на основании случайной выборки. В некоторых теориях статистического вывода за исходный пункт принимается правило: что, если нам ничего неизвестно о значении оцениваемого параметра, то следует принять, что каждое его значение равновозможно. Это ведет к истолкованию оцениваемого параметра как случайной переменной, характеризующейся прямоугольным распределением.

Нормальное распределение

Нормальное распределение играет основную роль в математической статистике. Это ни в малейшей степени не является случайным: в объективной действительности весьма часто встречаются различные признаки, значения которых распределяются по нормальному закону.

Если число дискретных событий возрастает, график на рисунке 3.2, представляющий разложение бинома (p+q) n , все более приближается к плавной кривой. Это приближение имеет место и для p = q, и для
p q. В последнем случае скошенность кривой при возрастании n уменьшается. При приближении n к бесконечности график кривой приближается к симметричной кривой. Пределом такого приближения биномиального распределения является нормальное распределение, выраженное формулой и графически изображаемое на рисунке 4.1.

В этом качестве, а именно в качестве непрерывной формы для предела биномиального распределения, нормальное распределение было открыто для р = q в 1733 г. А. Муавром (Англия). Обобщение его для p q сделано П. Лапласом (Франция) и К. Гауссом (Германия) в начале XIX в. Это открытие привело во второй половине XIX века к особому подчеркиванию значения нормального «закона» как модели, которой следуют распределения результатов наблюдений во всех естественных явлениях. Английский ученый К. Пирсон в начале XX в. показал, что нормальное распределение является одним из многих типов распределений, имеющихся в природе. Значение нормального распределения вследствие этого снизилось в сфере наблюдений, но возросло в теоретическом отношении, особенно в области теории выборок.

Рисунок 4.1 – Нормальное распределение

Уравнение нормальной кривой выражает зависимость теоретических численностей f(x) или у от значений x – непрерывно распределяющейся случайной величины. Оно пишется в различных формах.

Выражение, являющееся основной формой, относится к кривой с площадью, равной единице:

(4.6)

В этом уравнении f(x) – теоретические численности, выраженные в долях единицы, или плотности вероятности случайного события x;
s – квадратическое отклонение данного нормального распределения; π и е известные константы, π = 3,1426, е = 2,7183, s – отклонение случайно распределенной величины X от средней арифметической m, являющейся центром распределения величины X.

Вычислим математическое ожидание нормальной случайной переменной. Согласно определению (2.5):

(4.7)

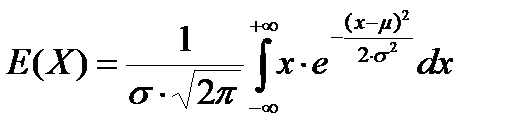
Для вычисления этого интеграла введем новую переменную:

, . Получим:

(4.8)

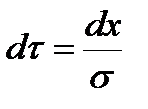
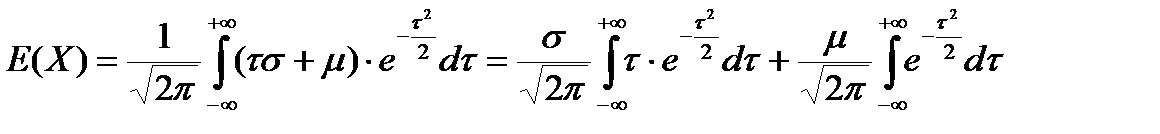
Интегрируя по частям, находим, что первый из приведенных выше интегралов равняется нулю. Далее, из математического анализа известно, что интеграл функции , взятый в границах (–∞, + ∞), равняется . Таким образом, получаем:

(4.9)

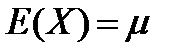
Следовательно, параметр μ есть математическое ожидание нормальной случайной переменной, плотность вероятности которой дается формулой (4.6).

Для вычисления дисперсии предварительно точно так же находим значение Е (X 2 ):

. (4.10)

Применив ту же подстановку, что при вычислении E(X), получим:

(4.11)

Интегрируя по частям, находим, что первый из интегралов в правой части формулы (4.11) равняется σ 2 , второй интеграл – нулю, а третий интеграл имеет значение μ 2 . Таким образом,

, откуда

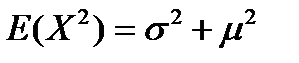
Итак, дисперсия нормальной случайной переменной равняется σ 2 , а ее среднее стандартное отклонение – σ.

Для удобства расчетов отклонение переменной X от m обычно выражают в единицах среднего стандартного отклонения s.

Выражение называют нормированным отклонением и обозначают его буквой t.

Тогда уравнение кривой нормального распределения в нормированной форме будет:

(4.12)

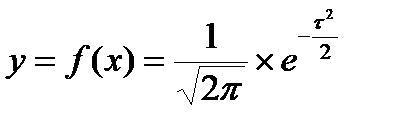
Оно выражает зависимость между вероятностью y и нормированным отклонением t. Средняя такого распределения m равна нулю, а квадратическое отклонение s = 1. Графически кривая нормального распределения изображена на рисунке 4.1. Максимального значения у достигает в начале координат, т. е. в точке, соответствующей центру распределения, где Х = t = 0, s = 1.

Максимальная ордината, обозначим ее y₀ = 1/2 × p = 0,39894. В других точках, т. е. при t ≠ 0, значения ординат y могут быть вычислены на основе формулы (4.12) путем логарифмирования.

На основе формулы (4.12) и данного анализа видно, что величина ординаты кривой нормального распределения может рассматриваться как функция нормированного отклонения t.

Кривая, показанная на рисунке 4.1, показывает, как плотности вероятностей (ординаты) растут до максимума в точке средней, т. е. в точке 0 и затем симметрично снижаются для значений у выше средней. Причем для X m +3s
(или t > 3) ординаты уже незначительно отличаются от нуля. Это означает, что наиболее вероятны те значения X, которые близки к m. По мере удаления от m значения X становятся все менее вероятными. Причем одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной Х от m равновероятны.

В точках m – s и m + s кривая нормального распределения или кривая плотности нормального распределения вероятностей имеет перегибы.

При определении ординат для какого-либо конкретного частного распределения ординаты, полученные по формуле (4.12), умножают на N/σ, где N – общий объем численностей, σ – выборочное квадратическое отклонение в единицах измерения распределенной величины X.

При изучении распределений как теоретической базы статистических заключений наибольший интерес представляет площадь под нормальной кривой. Эту площадь можно представить как интеграл от функции (4.12). Если интегрирование провести от начала координат, т. е. от нуля до любого значения, получим значение площади, заключенной между у₀ и значением у, соответствующим избранному τ. Математически функция площади от нормированного отклонения (обозначим ее F(t) при указанных пределах имеет выражение:

(4.13)

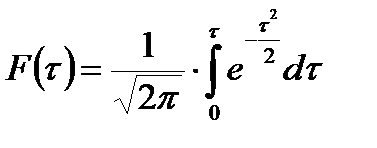
При таком предположении и нормальном распределении в совокупности, выражаемом формулой 4.13, можно определить вероятности встретить любые значения исследуемых объектов, т. е получить сумму вероятностей по 4.13.

Этот интеграл относится к разряду неберущихся. Поэтому в литературе приведена четырехзначная таблица площади под нормальной кривой в долях единицы, за которую принята вся площадь под кривой, либо при расчетах можно воспользоваться следующей аппроксимацией:

F(t) = 0,0164 τ 3 – 0,1564 τ 2 + 0,4917 τ – 0,0119

Найдем теоретическую относительную численность, т. е. вероятность объектов, имеющих диаметр от Х₁ = 12 до Х₂ = 22 см, μ = 30 см, σ = 6 см. Стандартизованные отклонения двух указанных значений X будут:

По таблице или представленной формуле F(–3) = 0,4986,
F(–1,33) = 0,4080. Отметим, что знак τ не имеет значения.

Разность F(τ₁) – F(τ₂) = 0,0904 означает вероятность встретить объекты указанного интервала X в общей совокупности, т. е. 9 объектов из 100.

Установим, пользуясь этим приемом, вероятности трех важных событий в теории выборок:

а) нормальная случайная переменная примет значение в интервале (μ – σ, μ + σ);

б) переменная примет значение в интервале (μ – 2σ, μ + 2σ);

в) она примет значение в интервале (–3σ, μ + 3σ).

Так как нормальная совокупность характеризуется μ = 0 и σ = 1, значения нормированного отклонения τ будут:

По таблице или формуле находим F(+1) = 0,3413, F(–1) = 0,3413, откуда вероятность события а), равная F(+l) + F(–l), составит 0,6826.

F(+2) = 0,4772, F(–2) = 0,4772, вероятность события б) равна 0,9544.

F(+3) = 0,4986, F(–3) = 0,4986, вероятность события в) равна 0,9972.

Эти результаты дают возможность утверждать, что в случае нормального распределения N (0; 1) 68% наблюдаемых значений отклоняются от среднего значения μ не более чем на величину стандартного отклонения σ, 95% значений не выйдут из пределов
μ ± 2σ и практически все значения уместятся в пределы μ ± 3σ. Вероятность отклонения за пределы 3σ равна 0,0026 ≈ 0,003, т. е. такое событие наступит только в среднем в 3 случаях из 1000 испытаний.

Видео:Парадокс Монти Холла просто и доступно | Теория вероятностей | ЛогикаСкачать

Теория вероятностей, формулы и примеры

О чем эта статья:

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Теория вероятностей | Математика TutorOnlineСкачать

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Дискретная случайная величина — величина, которая в результате испытания может принимать определенные значения с определенной вероятностью, то есть образовывать счетное множество.

Элементы множества можно пронумеровать. Они могут быть как конечными, так и бесконечными. Например: количество выстрелов до первого попадания в цель.

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Вероятностное пространство — это тройка (Ω, Σ, Ρ) иногда обрамленная угловыми скобками: ⟨ , ⟩ , где

• Ω — это множество объектов, которые называют элементарными событиями, исходами или точками.
• Σ — сигма-алгебра подмножеств , называемых случайными событиями;
• Ρ — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что .

Видео:Теория вероятностей #11: формула полной вероятности, формула БайесаСкачать

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Видео:Вся суть теории вероятностей — за 900 секунд!Скачать

Случайные события. Основные формулы комбинаторики

Видео:Математика это не ИсламСкачать

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

• Вероятность достоверного события равна единице.
• Вероятность невозможного события равна нулю.
• Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

• 0 ≤ P(A) ≤ 1.

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Видео:Теория вероятностей на пальцахСкачать

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

1. A — встреча с другом состоится, х и у — время прихода. Значит:
   0 ≤ х, у ≤ 60.
2. В прямоугольной системе координат этому условию удовлетворяют точки, которые лежат внутри квадрата ОАВС. Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то есть:

x−y y.

Этим неравенствам удовлетворяют точки из области G — то, что выделено красным:

Тогда вероятность встречи равна отношению площадей области G и квадрата:

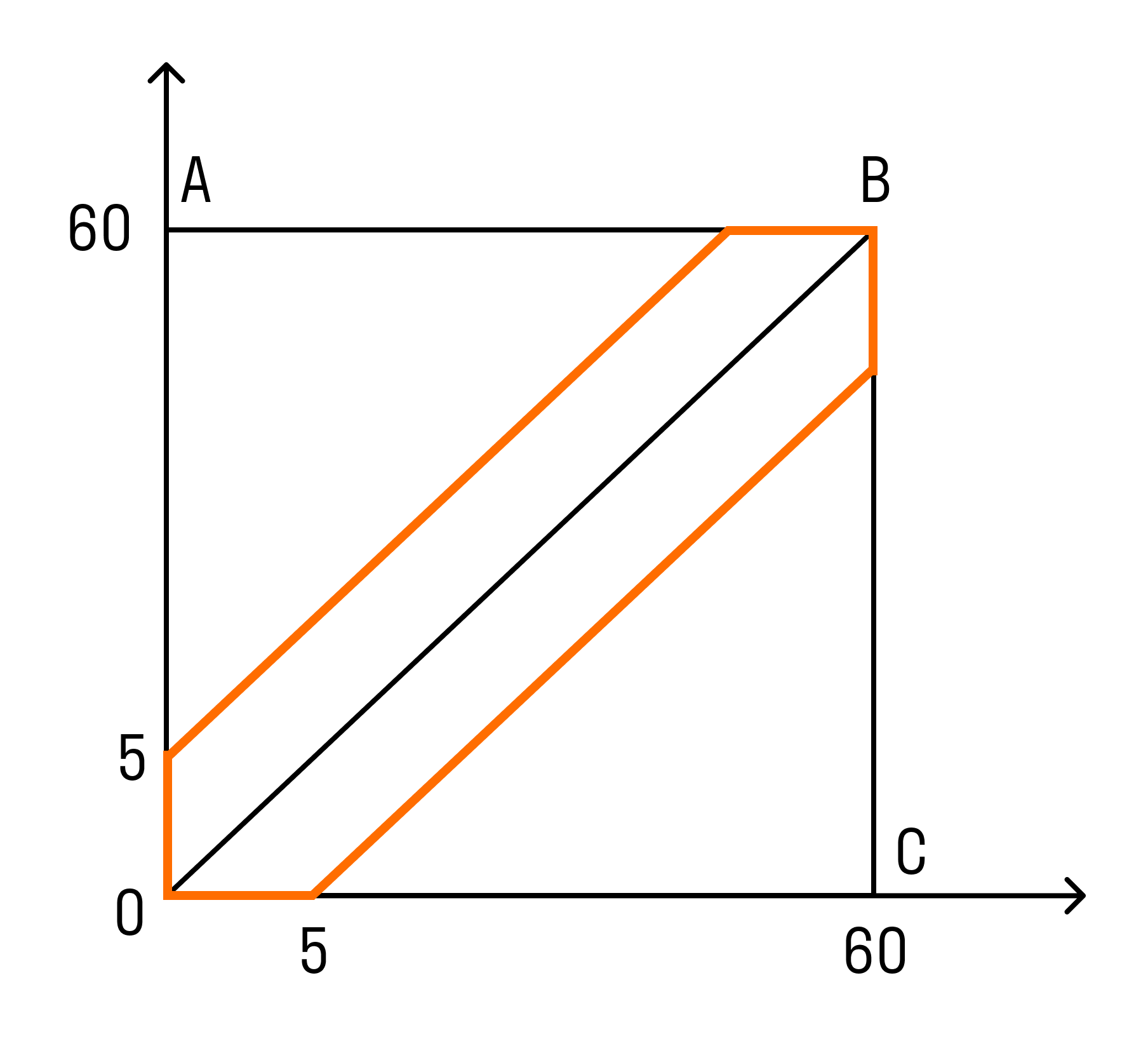
P(A)=S_G/S_OABC= 60 * 60 — 55 * 5560 * 60 = 23144 = 0,16

У нас есть отличные курсы по математике для учеников с 1 по 11 классы — приглашаем на вводный урок!

Видео:Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать

Сложение и умножение вероятностей

• Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
• События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
• Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

• P(A₁) + P(A₂) + … + P(A_n) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

1. только в одном справочнике;
2. только в двух справочниках;
3. во всех трех справочниках.

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1. 
2. 
3. 

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Видео:Математика без Ху!ни. Теория вероятностей. Схема БернуллиСкачать

Формула полной вероятности и формула Байеса

Если событие А может произойти только при выполнении одного из событий B₁, B₂, . B_n, которые образуют полную группу несовместных событий — вероятность события А вычисляется по формуле полной вероятности:

Вновь рассмотрим полную группу несовместных событий B₁, B₂, . B_n, вероятности появления которых P(B₁), P(B₂), . P(B_n). Событие А может произойти только вместе с каким-либо из событий B₁, B₂, . B_n, которые называются гипотезами. Тогда по формуле полной вероятности: если событие А произошло — это может изменить вероятности гипотез P(B₁), P(B₂), . P(B_n).

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

1. Возможны три гипотезы:
   • А1 — на линию огня вызван первый стрелок,
   • А2 — на линию огня вызван второй стрелок,
   • А3 — на линию огня вызван третий стрелок.

2. Так как вызов на линию огня любого стрелка равно возможен, то
   
3. В результате опыта наблюдалось событие В — после произведенных выстрелов мишень не поражена. Условные вероятности этого события при наших гипотезах равны:
   
4. По формуле Байеса находим вероятность гипотезы А₁ после опыта:
   

Видео:Как обмануть теорию вероятностей?Скачать

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

• Бросаем игральный кубик, где вероятности выпадения определенной цифры одинаковы в каждом броске.
• Включаем лампы с заранее заданной одинаковой вероятностью выхода из строя каждой.
• Лучник повторяет выстрелы по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой.

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Обозначим вероятность появления события А в единичном испытании буквой р, значит:

p = P(A), а вероятность противоположного события (событие А не наступило) — буквой q

q = P(¯A) = 1 — p.

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли:

P_n(k) = C_n k * p k * q n-k , где q = 1 — p.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Видео:Случайные величины | Теория вероятностейСкачать

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

np — q ≤ k ≤ np + p, где q=1−p

Так как np−q = np + p−1, то эти границы отличаются на 1. Поэтому k, являющееся целым числом, может принимать либо одно значение, когда np целое число (k = np), то есть когда np + p (а отсюда и np — q) нецелое число, либо два значения, когда np — q целое число.

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

1. По условию дано: n = 730, p = 1/365, g = 364/365
2. np — g = 366/365
3. np + p = 731/365
4. 366/365 ≤ m ≤ 731/365
5. m = 2

Видео:Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

1. По условию дано: n = 1000, p = 0,002, λ = np = 2, k = 3.
2. Искомая вероятность после подстановки в формулу:

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Видео:Теорема Байеса [3Blue1Brown]Скачать

Теоремы Муавра-Лапласа

Пусть в каждом из n независимых испытаний событие A может произойти с вероятностью p, q = 1 — p (условия схемы Бернулли). Обозначим как и раньше, через P_n(k) вероятность ровно k появлений события А в n испытаниях.

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

• 
• при больших x верно

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Видео:ПАРАДОКС РАЗДЕЛА СТАВКИ ИЛИ С ЧЕГО НАЧАЛАСЬ ТЕОРИЯ ВЕРОЯТНОСТЕЙ? == Vital MathСкачать

Закон прямоугольного треугольника теория вероятностей

AlexPM А почему Вы решили, что (M(X))^2 стоит под интегралом? потому что я невнимательная =)

так D(X) = 49/18 ? у нас же величина непрерывная. так??

а еще, раз уж преподаете теорию вероятностей, вы, наверное, знаете, что же такое закон распеределения прямоугольного треогульника.

ну, ваши вопросы — это круто, конечно. только мы моменты вообще не вычисляем. попробую, конечно, ответить, но учитывайте, что нам такого не читают. про второй момент рассказала true-devil в другой задаче =)

1. Начальным моментом порядка k СВ Х называетя мат.ожидание k-ой степени этой величины.

γ_k = сумма по i x_i^kp_i — для дискретной СВ

γ_k = ∫[-oo, +oo] x^k * f(x) dx — для непрерывной СВ

Центральным моментом порядка k называется μ_k = M(X — M(X))^k

2. во втрой формуле ∫[-oo, +oo] x^2 * f(x) dx — это начальный момент второго порядка для непрерывной СВ
а в первой D(X) — это и есть центральный момент второго порядка для непрерывной СВ //это я сама так думаю.. так что мало ли..)

4.Математическое ожидание — центр распределения СВ.
Мат. ожиданием называется сумма произведений всех значений СВ Х на вероятности: M(X) = cумма по i от 1 до n x_i* p_i.
Смысл мат. ожидания: M(X) является средним значением СВ.

Дисперсия — отклониние СВ от ее центра
Дисперсией СВ называется мат.ожидание квадратов ее отклонения от ее мат.ожидания.
D(X) = сумма по i (х_i— M(X))^2 *p_i
D(X) = M(X^2) — (M(X))^2 //мы только этой формулой пользовались
D(X) = cумма по i x_i^2 *p_i(cумма по i x_ip_i)

больше ничего не знаю!

Закон распределения прямоугольного треугольника — это выдумка российских изобретателей способов преподавания теории вероятностей для широкого круга слушателей. Изображает как раз такую плотность, как у Вас на рисунке. Среди общепринятых во всём мире названий распределений есть «треугольное» распределение, или распределение Симпсона. Его плотность вот такая: _/_ .

μ₁ = 0 почему, кстати?
Потому что
μ₁=M(X-M(X)) = M(X-γ₁) = (в силу линейности матожидания) = M(X) — M(γ₁) = γ₁ — γ₁ = 0.

Математическое ожидание — центр распределения СВ.
Центр тяжести, лучше сказать. Если значения случайной величины размазаны по прямой с плотностью f (килограмм массы размазан с какой-то плотностью), или массы p_i помещены в точки x_i, то точка, в которой можно эту прямую подвесить, чтобы она находилась в равновесии, как раз и будет матожиданием.

Ну молодец, видите, как много знаете. К этому обязательно следует добавлять знание свойств этих объектов: у матожидания и дисперсии много свойств, облегчающих их вычисление, мы некоторыми выше пользовались: если матожидания/дисперсии существуют, то
M(c*X)=c*M(X), где c — число,
M(X+Y)=M(X)+M(Y),
если a 2 *D(X),
D(c) = 0 (и наоборот, дисперсия нулевая только у постоянных),
если X,Y независимы, то D(X+Y)=D(X-Y)=D(X)+D(Y)
и т.п.

💥 Видео

Математика без Ху!ни. Сложение и умножение вероятностей. Формула полной вероятности.Скачать

Сферические треугольники и теория вероятностейСкачать

Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать

Вероятность за 120 секунд // Vital MathСкачать

Теория вероятностей #21: неравенство Чебышева, теорема Чебышева, теорема МарковаСкачать