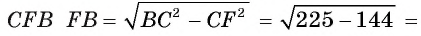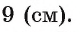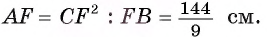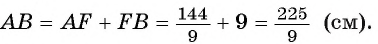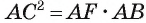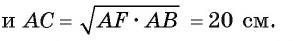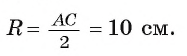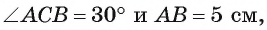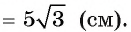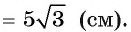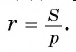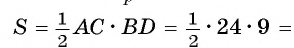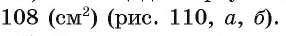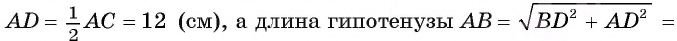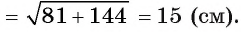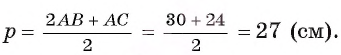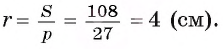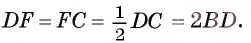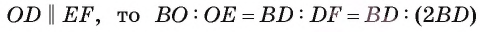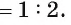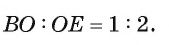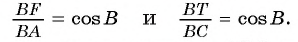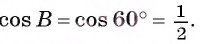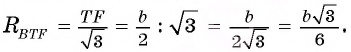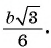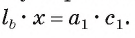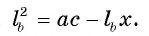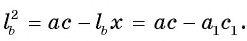Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов 2 и 4. Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.
а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.
б) Найдите площадь треугольника АСВ.
а) Введём обозначения, как показано на рисунке, пусть M, H, N — точки касания. Касательные, проведённые к окружности из одной точки равны: AM = AN, CM = CH, HB = BN. Поэтому:
откуда p = AM, где Р — периметр, p — полупериметр треугольника.
б) Для определения площади треугольника используем формулу, связывающую её с полупериметром, стороной и радиусом вневписанной окружности, касающейся этой стороны и продолжений двух других сторон треугольника:
Ответ: 
Примечание: указанная в решении формула легко может быть получена из следующих соображений 
где O1 — центр окружности с радиусом r1. При этом 
Тогда 
В остроугольном треугольнике ABC проведены высоты AP и CQ.
а) Докажите, что угол PAC равен углу PQC.
б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и ∠ABC = 60°.
а) Углы APC и AQC — прямые, значит, точки A, Q, P и C лежат на одной окружности с диаметром AC, и, следовательно, равны и вписанные углы PAC и PQC этой окружности, опирающиеся на дугу PC, что и требовалось доказать.
б) Прямоугольные треугольники ABP и CBQ имеют общий угол ABC, следовательно, они подобны, откуда 
или 
но тогда и треугольники BAC и BPQ также подобны, причем коэффициент подобия равен 
откуда 
Тогда радиус R окружности, описанной около треугольника ABC равен 
Ответ: 
В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что 
и ∠KMN = 45°.
а) Углы NAK и NBK, опирающиеся на отрезок KN, равны, значит, точки A, B, N и K лежат на одной окружности, а, следовательно, равны и вписанные углы ABK и ANK этой окружности, опирающиеся на дугу AK, что и требовалось доказать.
б) Прямоугольные треугольники KMB и NMA имеют общий угол KMN, следовательно, они подобны, откуда 
или 
но тогда и треугольники KMN и BMA также подобны, причем коэффициент подобия равен 
откуда
Тогда радиус R окружности, описанной около треугольника ABM равен
Ответ: 
Точка О — центр окружности, вписанной в треугольник ABC. На продолжении отрезка AO за точку О отмечена точка K так, что BK = OK.
а) Докажите, что четырехугольник ABKC вписанный.
б) Найдите длину отрезка AO, если известно, что радиусы вписанной и описанной окружностей треугольника ABC равны 3 и 12 соответственно, а OK = 5.
а) Пусть 
Так как 
— центр вписанной окружности треугольника ABC, то 
— биссектрисы углов 
и 
значит, 
Угол BOK внешний для треугольника AOB, поэтому 
(см. рисунок).
Так как 
(по построению), то 
тогда 
Углы CBK и KAC опираются на один и тот же отрезок CK и равны друг другу: 
Тогда по признаку, связанному со свойством вписанных углов, точки 
лежат на одной окружности.
б) Обозначим через 
радиусы вписанной и описанной окружностей треугольника 
Пусть H — проекция точки O на сторону AB (см. рис.), тогда 
Так как точки 
лежат на одной окружности, то радиус описанной окружности треугольника ABK совпадает с радиусом описанной окружности треугольника 
и равен 
Из треугольника ABK по теореме синусов: 
Тогда
Так как 
то 
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Треугольники и окружность — задачи с примерами решения
Пример:
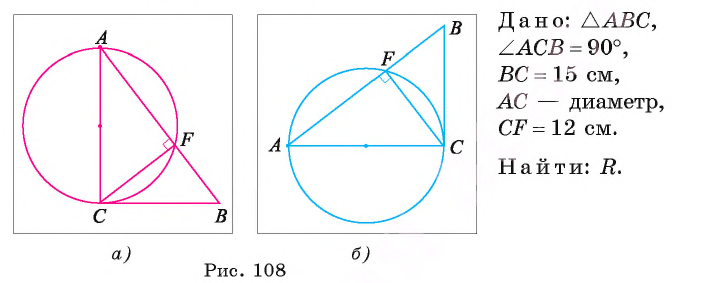
Длина катета ВС прямоугольного треугольника АСВ равна 15 см, а его катет АС является диаметром окружности, которая пересекает гипотенузу в точке F, CF =12 см. Вычислите радиус окружности.
Решение:
Из условия следует, что радиус R равен половине катета АС. Заметим, что
1) В треугольнике 
2) Воспользовавшись равенством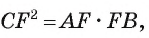 
найдем 
3) Теперь
4) Квадрат длины катета прямоугольного треугольника равен произведению длины гипотенузы и длины проекции этого катета на гипотенузу, следовательно, 
Таким образом, 
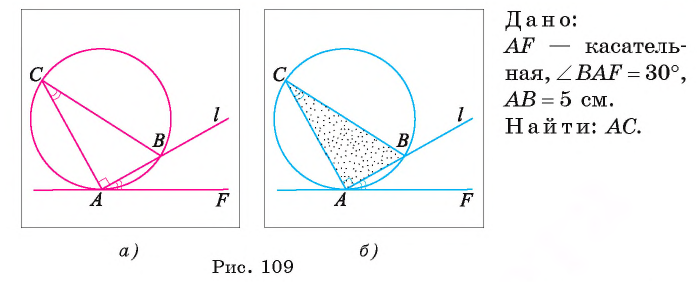
Пример:
Решение:
По теореме об угле между хордой и касательной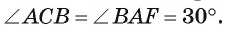 
Так как точки С и В диаметрально противоположные, то угол САВ опирается на диаметр, а следовательно, он прямой, т. е. треугольник САВ — прямоугольный (рис. 109, а, б). Расстояние от точки С до точки касания А равно длине катета СА треугольника САВ. Так как
Ответ 
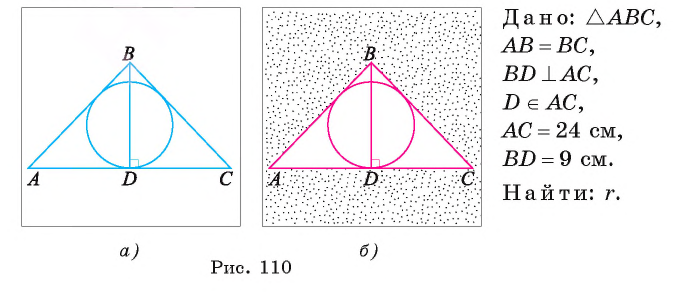
Пример:
Вычислите радиус окружности, вписанной в равнобедренный треугольник ABC, если длина его основания АС равна 24 см, а высота BD, проведенная к основанию, равна 9 см.
Решение:
Для вычисления радиуса г вписанной окружности воспользуемся формулой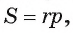 
где S — площадь треугольника, р — его полупериметр. Отсюда получим 
1) Площадь треугольника
2) В прямоугольном треугольнике ADB длина катета
3) Теперь полупериметр 
4) Таким образом, найдем 
Пример:
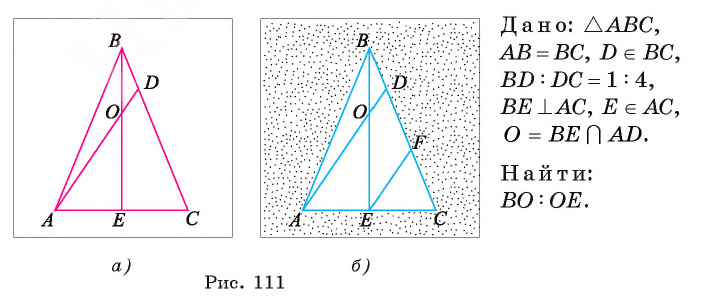
В равнобедренном треугольнике ABC с основанием АС на стороне ВС лежит точка D так, что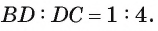 
В каком отношении точка О пересечения отрезка AD и высоты BE делит высоту BE, считая от вершины В?
Решение:
1) Так как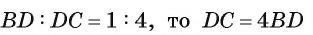 
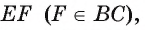
(рис. 111, а, б). Проведем отрезок 
, параллельный отрезку AD.
2) Так как высота, проведенная к основанию равнобедренного треугольника, является медианой, то точка Е — середина стороны АС.
3) По признаку средней линии отрезок EF — средняя линия треугольника ADC, значит,
4) Так как 
Ответ: 
Пример:
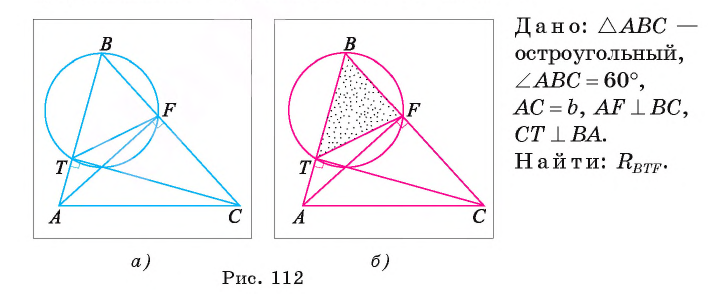
Отрезки AF и СТ — высоты остроугольного треугольника ABC. Найдите радиус окружности, описанной около треугольника BTF, если A ABC = 60° и АС = b.
Решение:
Воспользуемся теоремой синусов и тем, что треугольник ABC подобен треугольнику BTF.
1) В треугольнике BTF по теореме синусов выполняется равенство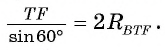
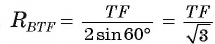
Следовательно, 
(рис. 112, a, 6).
2) Рассмотрим треугольники ABC и FTC. Эти треугольники подобны. Действительно, 
Следовательно,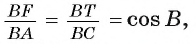
т.е. треугольники подобны с коэффициентом подобия 
3) Из подобия треугольников ABC и FTC следует, что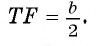 
Таким образом, 
Ответ: 
Пример:
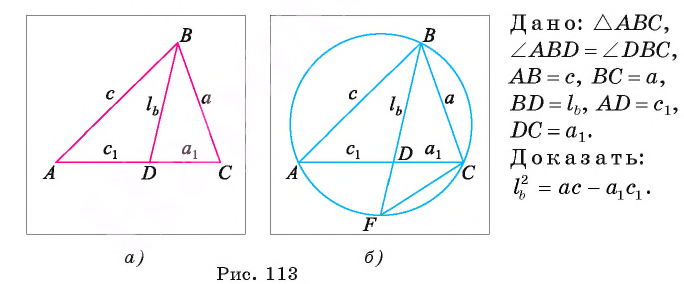
Отрезок BD — биссектриса треугольника ABC. Известно, что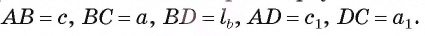 
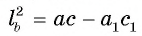
Докажите, что 
(рис. 113, а).
Рассмотрим окружность, описанную около треугольника ABC. Пусть прямая BD пересекает окружность в точке F и DF = х (рис. 113, б).
1) По свойству отрезков пересекающихся хорд выполняется равенство
2) Треугольники ABD и FBC подобны, так как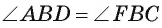 
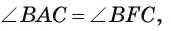
по условию и 
поскольку являются вписанными в окружность и опираются на одну и ту же дугу.
3) Из подобия треугольников ABD и FBC следует, что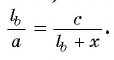 
Отсюда 
3) Таким образом,
Что и требовалось доказать.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
- Описанные и вписанные окружности
- Пространственные фигуры — виды, изображения, свойства
- Взаимное расположения прямых на плоскости
- Треугольник
- Решение треугольников
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Треугольники. Практическая часть - решение задачи. 7 класс.Скачать
Классификация задач на вписанные в треугольник и описанные около треугольника окружности
Разделы: Математика
Задачи на вписанные в треугольник и описанные около треугольника окружности вызывают даже у сильных учащихся затруднения при их решении. Попытка провести классификацию этих задач по содержанию и методам решения привела к положительным результатам. Учащиеся полюбили этот тип задач. Хотим поделиться нашим опытом.
- Замечательное открытие: люди изобрели колесо.
- Окружность, описанная около треугольника.
- Окружность, вписанная в треугольник.
- Задачи на вписанные и описанные окружности.
На востоке от Аравийского полуострова с севера на юг текут две большие реки – Евфрат и Тигр. Между ними тянется узкая длинная полоса земли. В древности она называлась Месопотамией, что в переводе означает “ Междуречье’’. Самым известным государством Месопотамии был Вавилон. Земля в Междуречье плодородная, но там не было ни металлов, ни камня, ни леса, чтобы строить дома. Всё это вавилонянам приходилось покупать у других народов. Поэтому Вавилон раньше других стран стал вести большую торговлю. Торговля помогала науке. В математике вавилонские учёные добились больших успехов.
Около шести тысяч лет назад в Вавилоне было сделано замечательное открытие: люди изобрели колесо. Колесо? Что же тут замечательного? Но так кажется только на первый взгляд. Представьте себе на секунду, что вдруг случилось чудо, и на земле исчезли все колёса. Это было бы настоящей катастрофой! Остановятся автомобили и поезда, замрут заводы и фабрики, перестанут давать ток электростанции. Выходит, что неизвестный вавилонский изобретатель первого колеса действительно сделал великое открытие.
Вавилонские инженеры и мастера стали пользоваться блоками. Они поднимали и перетаскивали такие тяжести, справиться с которыми без колеса было бы не под силу. Колесо и рычаг стали первыми настоящими помощниками человека в работе с большими тяжестями.Так изобретение колеса сыграло очень большую роль в истории Вавилона.
Окружность называется описанной около многоугольника, если все вершины многоугольника лежат в окружности.
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.
Теорема. Около любого треугольника можно описать окружность.
Доказательство: Рассмотрим произвольный В треугольник АВС. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведём отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА=ОВ=ОС. Поэтому окружность с центром О радиуса ОА проходит через О все три вершины треугольника и, значит, является описанной около треугольника АВС.
Вывод: Центр описанной около треугольника окружности лежит А С на пересечении серединных перпендикуляров и расположен:
а) в треугольнике, если он остроугольный;
б) на середине гипотенузы, если он прямоугольный;
в) вне треугольника, если он тупоугольный.
Рассмотрим задачи на нахождение радиуса описанной около треугольника окружности. (См. Приложение1.)
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.
Теорема. В любой треугольник можно вписать окружность.
Доказательство: Рассмотрим произвольный треугольник АВС и обозначим М буквой О точку пересечения его биссектрис. Проведём из точки О перпендикуляры А К В ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА.
Так как точка О равноудалена A k B от сторон треугольника АВС то ОК = ОL=ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М.
Стороны треугольника АВС касаются этой окружности в точках К, L и М, так как они перпендикулярны к радиусам ОК, ОL и ОМ.
Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС.
Выводы. Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис треугольника. Касательная к окружности (стороны треугольника) перпендикулярна к радиусу, проведённому в точку касания.
Рассмотрим задачи на нахождение радиуса вписанной в треугольник окружности.
Задачи на вписанную и описанную окружность. (См. Приложение 3.)
💥 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать
Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать
Найдите угол: задача по геометрииСкачать
🔥 ФОКУС с треугольником #shortsСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать
Две задачи по геометрии за 7 класс на тему: "Треугольники"Скачать
Задача, которую исключили из экзамена в АмерикеСкачать
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать
Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать
Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать
Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать
Вписанная и описанная окружности | Лайфхак для запоминанияСкачать
Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать
Задача, которую боятсяСкачать
Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
