Задачи с хордами окружности огэ

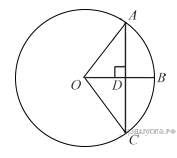
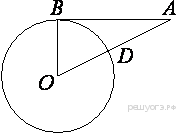
Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.

Найдем отрезок DO: DO = OB − BD = 5 − 1 = 4. Так как OB перпендикулярен AC, треугольник AOD — прямоугольный. По теореме Пифагора имеем: . Треугольник AOC — равнобедренный так как AO = OC = r, тогда AD = DC. Таким образом, AC = AD·2 = 6.

Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности.

Проведем радиусы OA и OB. Так как по условию задачи хорда AB равна радиусу, то треугольник AOB — равносторонний, следовательно, все его углы равны 60°. Угол AOB — центральный и равен 60° Угол ACB — вписанный и опирается на ту же дугу, что и угол AOB. Таким образом,

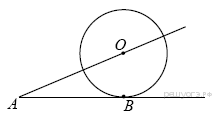
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB. Из теоремы Пифагора:

В треугольнике ABC угол C равен 90°, AC = 30 , BC = Найдите радиус окружности, описанной около этого треугольника.

Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы. По теореме Пифагора имеем:

Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.

Проведём построение и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и HOB, они прямоугольные, OH — общая, AO и OB равны как радиусы окружности, следовательно, эти треугольники равны, откуда По теореме Пифагора найдём радиус окружности:

Диаметр равен двум радиусам, следовательно,

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Задачи про хорды окружности огэ

Видео:ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ХОРДЫ В ОКРУЖНОСТИСкачать

Задачи про хорды окружности огэ

Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.

Найдем отрезок DO: DO = OB − BD = 5 − 1 = 4. Так как OB перпендикулярен AC, треугольник AOD — прямоугольный. По теореме Пифагора имеем: . Треугольник AOC — равнобедренный так как AO = OC = r, тогда AD = DC. Таким образом, AC = AD·2 = 6.

Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности.

Проведем радиусы OA и OB. Так как по условию задачи хорда AB равна радиусу, то треугольник AOB — равносторонний, следовательно, все его углы равны 60°. Угол AOB — центральный и равен 60° Угол ACB — вписанный и опирается на ту же дугу, что и угол AOB. Таким образом,

К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB. Из теоремы Пифагора:

В треугольнике ABC угол C равен 90°, AC = 30 , BC = Найдите радиус окружности, описанной около этого треугольника.

Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы. По теореме Пифагора имеем:

Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.

Проведём построение и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и HOB, они прямоугольные, OH — общая, AO и OB равны как радиусы окружности, следовательно, эти треугольники равны, откуда По теореме Пифагора найдём радиус окружности:

Диаметр равен двум радиусам, следовательно,

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задания для подготовки к ОГЭ по теме «Касательная, хорда, секущая, радиус.»

Материалы составлены из заданий Образовательного портала для подготовки к экзаменам СДАМ ГИА Дмитрия Гущина. В работе подобраны прототипы Задания№10 Окружность, круг и их элементы для подготовки к ОГЭ по математике 9 класс модуль»Геометрия» по теме «Касательная, хорда, секущая, радиус». Перед решением этих задач необходимо повторить понятия касательной, секущей, хорды и их свойств, понятия радиуса и диаметра. Повторить теорему Пифагора, свойства равнобедренного треугольника.

Просмотр содержимого документа
«Задания для подготовки к ОГЭ по теме «Касательная, хорда, секущая, радиус.»»

Задание №10. Касательная, хорда, секущая, радиус.

К окруж­но­сти с цен­тром в точке О прове­де­ны касательная AB и секу­щая AO. Най­ди­те радиус окружности, если AB = 12 см, AO = 13 см.

К окруж­но­сти с цен­тром в точке О прове­де­ны касательная AB и секу­щая AO. Най­ди­те радиус окружности, если AB = 14 см, AO = 50 см.

Ра­ди­ус OB окруж­но­сти с центром в точке O пе­ре­се­ка­ет хорду AC в точке D и перпенди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ради­ус окруж­ности равен 5 см.

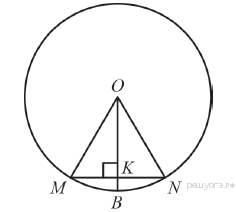
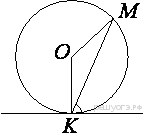
Ра­ди­ус OB окруж­но­сти с центром в точке O пе­ре­се­ка­ет хорду MN в её середи­не — точке K. Най­ди­те длину хорды MN, если KB = 1 см, а ра­ди­ус окруж­но­сти равен 13 см.

Длина хорды окруж­но­сти равна 72, а расстояние от цен­тра окруж­но­сти до этой хорды равно 27. Най­ди­те диа­метр окружности.

Длина хорды окруж­но­сти равна 96, а расстояние от цен­тра окруж­но­сти до этой хорды равно 20. Най­ди­те диа­метр окруж­но­сти.

Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM образует с касательной угол, рав­ный 83°. Най­ди­те величи­ну угла OMK. Ответ дайте в градусах.

Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окружности. Хорда KM образу­ет с ка­са­тель­ной угол, равный 60°. Найди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM образу­ет с ка­са­тель­ной угол, равный 79°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окружно­сти. Най­ди­те длину хорды CD, если AB = 20, а рас­сто­я­ния от цен­тра окружно­сти до хорд AB и CD равны соответ­ствен­но 24 и 10.

От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окружно­сти. Най­ди­те рас­сто­я­ние от цен­тра окруж­но­сти до хорды CD, если AB = 12, CD = 16, а рас­сто­я­ние от центра окруж­но­сти до хорды AB равно 8.

От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окружно­сти. Най­ди­те рас­сто­я­ние от цен­тра окруж­но­сти до хорды CD, если AB = 18, CD = 24, а рас­сто­я­ние от центра окруж­но­сти до хорды AB равно 12.

От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окружно­сти. Най­ди­те рас­сто­я­ние от цен­тра окруж­но­сти до хорды CD, если AB = 24 , CD = 32, а рас­сто­я­ние от цен­тра окружности до хорды AB равно 16.

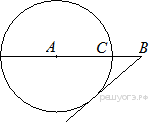
От­ре­зок AB = 40 ка­са­ет­ся окруж­но­сти радиу­са 75 с цен­тромO в точке B. Окружность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­дите AD.

От­ре­зок AB = 48 ка­са­ет­ся окруж­но­сти радиу­са 14 с цен­тромO в точке B. Окружность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

На от­рез­ке AB вы­бра­на точка C так, что AC = 75 и BC = 10. По­стро­е­на окружность с цен­тром A, про­хо­дя­щая через C. Най­ди­те длину от­рез­ка касательной, про­ведённой из точки B к этой окруж­но­сти.

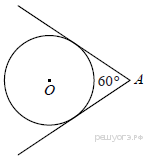
Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 6.

Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Касательная и хорда. Подготовка к ОГЭ и ЕГЭ
материал для подготовки к егэ (гиа) по геометрии (9 класс)

Данную пезентацию можно использовать при подготовке к ЕГЭ и ОГЭ

Видео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Скачать:

Предварительный просмотр:

Видео:Свойства хорд, касательных, секущих окружности I Для решения задач из ОГЭ И ЕГЭ I Часть 1Скачать

Подписи к слайдам:

Подготовка к ОГЭ Задние №10 Тема: « Касательная,хорда,секущая , радиус.»
?redir=1

Повторим теоремы по этой теме. D B A C C₁ α 1.Угол между касательной и хордой,проходящей через точку касания,измеряется половиной заключённой в нём дуги.

E C A D B 2.Произведение отрезков одной из двух пересекающихся хорд равно произведению отрезков другой хорды.

M B C A D K L 3.Угол между двумя пересекающимися хордами измеряется суммой заключенной между ними дуг.

. B A M P Q 4.Угол между двумя секущими ,проведенными из одной точки ,измеряется полуразностью заключенных между ними дуг.

2 ) M K A B 1 5.Угол между касательной и секущей ,проведенными из одной точки ,измеряется полуразностью заключенных внутри него дуг.

) M L K 6. Угол между двумя касательными ,проведенными из одной точки ,равен 180⁰ минус величина заключенной внутри него дуги,меньшей полуокружности.

О М N K 30⁰ ₍ 15 H Найти: MN=? Проведем прямую от точки М в точку N. ∠MKO= 30⁰ , ∠ MKO= 90⁰ =› ∠ HMK = 60⁰ ∠ HKN = ∠MKH = 60⁰ ∠KMH=∠MKN=60⁰=›∠HNK=180⁰-(KMH+MKN)=60⁰ Из этого сделаем вывод,что ▲ MNK- равносторонний =› MK=MN=15. Ответ: MN=15.

Задача 2. О M N 12 15 Дано : ON=15 Найти: MN=? Рассмотрим ▲ MON ∠ OMN= 90⁰=› ▲ MON- прямоугольный ON- гипотенуза MO- катет Найдем MN: MN= ON²-OM²= √225-√144 =√81=9 Ответ: MN=9

Задача 3 O M N K 10 10 > 16 Дано: OM=ON=10 MN=16 Найти: OK=? Рассмотрим ▲ MON OM=ON=10( по условию) => ▲ MON- равнобедренный OK- медиана проведенная к основанию => что NK=KN=8 Рассмотрим ▲ OKM: т.к OK- медиана проведенная к основанию,то она еще и высота=> ∠ OKM=90⁰=>▲OKM- прямоугольный; MO- биссектриса =10 KM- катет=8 Найдем OK: OK= OM²-MK²= √100-√64=√16=4 Ответ: OK=4

о А В С Задача 4 Дано: ка­са­тель­ные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 72⁰ Т.к касательные проведены из одной точки ,то они равны => AB=CB => ▲ ABC –равнобедренный. От­ку­да ∠CAB=∠CBA=180⁰-∠ACB =54⁰ 2 Угол между ка­са­тель­ной и хор­дой равен по­ло­ви­не дуги, ко­то­рую он за­клю­ча­ет, зна­чит, дуга AB равна 108⁰ ∠AOB- центраельный и равен дуге,на которую опирается=> ∠AOB= 108⁰ Рассмотрим ▲ OAB;OA=OB т.к радиусы=> ▲OAB- равнобедренный; =>∠ABO= 180⁰-108⁰ = 36⁰ Найти:∠ ABO

Задача 5 О С В А а Ответ: ∠ ACB= 30 ⁰ Найдите величину (в градусах ) угла α, опирающегося на хорду AB ,равную градусу окружности. Решение: Про­ве­дем ра­ди­у­сы OA и OB. Так как по усло­вию за­да­чи хорда AB равна ра­ди­у­су, то тре­уголь­ник AOB — рав­но­сто­рон­ний, сле­до­ва­тель­но, все его углы равны 60°. ∠AOB — цен­траль­ный и равен 60° Угол ACB — впи­сан­ный и опи­ра­ет­ся на ту же дугу, что и ∠ AOB. Таким об­ра­зом, ∠ ACB= 60⁰:2=30⁰

Задача 6 Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окруж­но­сти равен 5 см. O D A B C Н ай­дем от­ре­зок DO: DO = OB − BD = 5 − 1 = 4. Так как OB пер­пен­ди­ку­ля­рен AC, тре­уголь­ник AOD — пря­мо­уголь­ный. По тео­ре­ме Пи­фа­го­ра имеем : AD = √ AO²- √OD² =√25- √16=3 . Тре­уголь­ник AOC — рав­но­бед­рен­ный так как AO = OC = r, тогда AD = DC. Таким об­ра­зом, AC = AD·2 = 6.

Задача 7 К окруж­но­сти с цен­тром в точке O про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO . Най­ди­те ра­ди­ус окруж­но­сти, если , AB =21, AO=75 . A B O Со­еди­ним от­рез­ком точки O и B; по­лу­чен­ный от­ре­зок — ра­ди­ус, про­ведённый в точку ка­са­ния, по­это­му OB пер­пен­ди­ку­ля­рен AB. За­да­ча сво­дит­ся к на­хож­де­нию ка­те­та OB пря­мо­уголь­но­го тре­уголь­ни­ка AOB: по тео­ре­ме Пи­фа­го­ра равен: √75²-√ 21²=72

Задача 8 Сто­ро­на AC тре­уголь­ни­ка ABC про­хо­дит через центр опи­сан­ной около него окруж­но­сти. Най­ди­те ∠C , если ∠A = 44. Ответ дайте в гра­ду­сах. O A B D Ре­ше­ние. Угол ABC − пря­мой, так как он впи­сан­ный и опи­ра­ет­ся на диа­метр. Сле­до­ва­тель­но тре­уголь­ник ABC − пря­мо­уголь­ный, а ∠ C= 90-44=46 Ответ: 46.

Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

По теме: методические разработки, презентации и конспекты

открытый урок алгебры в 11 классе. Касательная. Уравнение касательной

урок алгебры в 11 классе по теме: «Касательная. Уравнение касательной»1. Тип урока: Урок изучения нового материала 2. Цели урока: · Уточнить понятие «касательной». · Вывести уравнение касател.

Углы между касательной к окружности и хордой, проведенной в точку касания

Цель урока: сформулировать и доказать свойства еще одного вида углов, связанных с понятием окружности – углов между касательной к окружности и хордой, проведенной в точку касания.Задачи урока: .

Урок по теме «Касательная. Уравнение касательной»

Урок по теме «Касательная. Уравнение касательной» Тип урока: изучение нового материала.Методы обучения: наглядный, частично поисковый.Цель урока:Ввести понятие касательной к графику функции в точке, в.

Подготовка к ОГЭ: обучающая работа по теме «Касательная, хорда, секущая, радиус»

Данная работа содержит типовые задачи ОГЭ по теме «Касательная, хорда, секущая, радиус» с подробным решением. К каждому типу задачи предложены 9 вариантов для самостоятельной работы. .

Презентация к уроку «Касательная. Уравнение касательной»

Касательная.Уравнение касательной»11 класс.

Самостоятельная работа 8 класс «Касательная.Свойства пересекающихся хорд. Центральный и вписанный углы»

Самостоятельная итоговая работа состоит из 2-х вариантов разного уровня сложности: 1 вариант простой, 2 вариант — сложный. Это позволит провести срез ЗУН учащихся по темам с разным уровнем подготовки.

Видео:Демо ОГЭ по математике. Задание 17. Хорда окружности.Скачать

Задания для подготовки к ОГЭ по теме «Касательная, хорда, секущая, радиус.»

Материалы составлены из заданий Образовательного портала для подготовки к экзаменам СДАМ ГИА Дмитрия Гущина. В работе подобраны прототипы Задания№10 Окружность, круг и их элементы для подготовки к ОГЭ по математике 9 класс модуль»Геометрия» по теме «Касательная, хорда, секущая, радиус». Перед решением этих задач необходимо повторить понятия касательной, секущей, хорды и их свойств, понятия радиуса и диаметра. Повторить теорему Пифагора, свойства равнобедренного треугольника.

Просмотр содержимого документа
«Задания для подготовки к ОГЭ по теме «Касательная, хорда, секущая, радиус.»»

Задание №10. Касательная, хорда, секущая, радиус.

К окруж­но­сти с цен­тром в точке О прове­де­ны касательная AB и секу­щая AO. Най­ди­те радиус окружности, если AB = 12 см, AO = 13 см.

К окруж­но­сти с цен­тром в точке О прове­де­ны касательная AB и секу­щая AO. Най­ди­те радиус окружности, если AB = 14 см, AO = 50 см.

Ра­ди­ус OB окруж­но­сти с центром в точке O пе­ре­се­ка­ет хорду AC в точке D и перпенди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ради­ус окруж­ности равен 5 см.

Ра­ди­ус OB окруж­но­сти с центром в точке O пе­ре­се­ка­ет хорду MN в её середи­не — точке K. Най­ди­те длину хорды MN, если KB = 1 см, а ра­ди­ус окруж­но­сти равен 13 см.

Длина хорды окруж­но­сти равна 72, а расстояние от цен­тра окруж­но­сти до этой хорды равно 27. Най­ди­те диа­метр окружности.

Длина хорды окруж­но­сти равна 96, а расстояние от цен­тра окруж­но­сти до этой хорды равно 20. Най­ди­те диа­метр окруж­но­сти.

Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM образует с касательной угол, рав­ный 83°. Най­ди­те величи­ну угла OMK. Ответ дайте в градусах.

Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окружности. Хорда KM образу­ет с ка­са­тель­ной угол, равный 60°. Найди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM образу­ет с ка­са­тель­ной угол, равный 79°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окружно­сти. Най­ди­те длину хорды CD, если AB = 20, а рас­сто­я­ния от цен­тра окружно­сти до хорд AB и CD равны соответ­ствен­но 24 и 10.

От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окружно­сти. Най­ди­те рас­сто­я­ние от цен­тра окруж­но­сти до хорды CD, если AB = 12, CD = 16, а рас­сто­я­ние от центра окруж­но­сти до хорды AB равно 8.

От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окружно­сти. Най­ди­те рас­сто­я­ние от цен­тра окруж­но­сти до хорды CD, если AB = 18, CD = 24, а рас­сто­я­ние от центра окруж­но­сти до хорды AB равно 12.

От­рез­ки AB и CD яв­ля­ют­ся хор­да­ми окружно­сти. Най­ди­те рас­сто­я­ние от цен­тра окруж­но­сти до хорды CD, если AB = 24 , CD = 32, а рас­сто­я­ние от цен­тра окружности до хорды AB равно 16.

От­ре­зок AB = 40 ка­са­ет­ся окруж­но­сти радиу­са 75 с цен­тромO в точке B. Окружность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­дите AD.

От­ре­зок AB = 48 ка­са­ет­ся окруж­но­сти радиу­са 14 с цен­тромO в точке B. Окружность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

На от­рез­ке AB вы­бра­на точка C так, что AC = 75 и BC = 10. По­стро­е­на окружность с цен­тром A, про­хо­дя­щая через C. Най­ди­те длину от­рез­ка касательной, про­ведённой из точки B к этой окруж­но­сти.

Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 6.

🔥 Видео

Окружность, диаметр, хорда геометрия 7 классСкачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

ОГЭ математика 10 минут на подготовку. Задание 16 касательная хорда секущаяСкачать

Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать

Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать

ищем хорду в окружности. огэ 1 часть геометрияСкачать

ОГЭ Задание 16 Окружность, радиус, диаметрСкачать

Задача на нахождение длины хорды окружностиСкачать

Пересекающиеся хорды окружности. Решишь задачу?Скачать

ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать