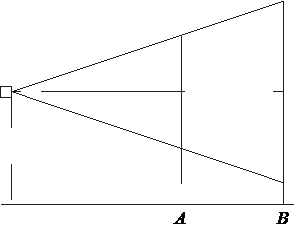
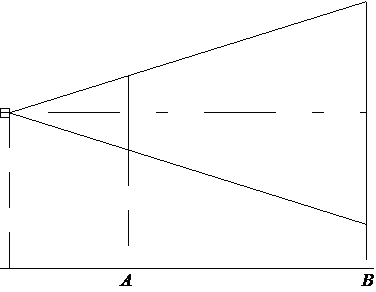
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Заметим, что высота экрана, расположенного на расстоянии 250 см, в 2 раза меньше высоты экрана, расположенного на искомом расстоянии, значит, по теореме о средней линии, искомое расстояние в два раза больше первоначального экрана: 250·2 = 500.
Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?
Столб и человек образуют два прямоугольных треугольниках ABC и FEB. Эти треугольники подобны по двум углам. Пусть высота фонаря равна тогда, поскольку расстояние от фонаря до конца тени равно 12 шагов, получаем:
откуда
- Подобие. Задачи для подготовки к ОГЭ.
- Просмотр содержимого документа «Подобие. Задачи для подготовки к ОГЭ.»
- Открытый банк заданий ОГЭ на подобие треугольников
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 🔥 Видео
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Подобие. Задачи для подготовки к ОГЭ.
Задачи подобраны с сайта «ФИПИ» в двух вариантах.
Просмотр содержимого документа
«Подобие. Задачи для подготовки к ОГЭ.»
Подобие (ОГЭ) Вариант 1
Подобие (ОГЭ) Вариант 2
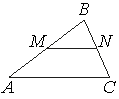
Прямая, параллельная стороне AC
треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=76,
AC=38, MN=28. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44,
MN=24. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21,
MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно,
AC=18, MN=8. Площадь треугольника ABC
равна 81. Найдите площадь треугольника MBN.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=12, DC=48, AC=35.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=10, DC=25, AC=56.
Человек стоит на расстоянии 12 м от столба, на котором на высоте 6,4 м висит фонарь. Человек отбрасывает тень длиной 4 м. Найдите рост человека в сантиметрах.
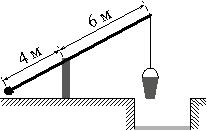
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Проектор полностью освещает экран A высотой 80 см, расположенный
на расстоянии 250 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 240 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
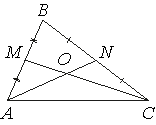
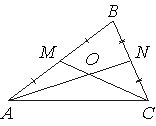
Точки M и N являются серединами сторон AB и BC треугольника ABC
соответственно. Отрезки AN и CM
пересекаются в точке O, AN=12,
CM=15. Найдите CO.
Точки M и N являются серединами сторон AB и BC треугольника ABC
соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=9. Найдите CO.
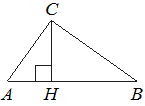
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=16. Найдите CH.
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=5, BH=20. Найдите CH.
Основания BC и AD трапеции ABCD равны соответственно
5 и 45, BD=15. Докажите, что треугольники CBD и BDA подобны.
Основания BC и AD трапеции ABCD равны соответственно
4 и 64, BD=16. Докажите, что треугольники CBD и BDA подобны.
В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
В треугольнике ABC с тупым углом BAC проведены высоты BB1 и CC1. Докажите, что треугольники AB1C1 и ABC подобны.
Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Открытый банк заданий ОГЭ на подобие треугольников
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Открытый банк заданий ОГЭ на подобие треугольников МБОУ «Суксинская средняя общеобразовательная школа Высокогорского муниципального района Республики Татарстан» Гарипов Рафаэль Насихович, 1 кв. категория
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
Решение х метров- расстояние от человека до фонаря 9/2 = (х+1)/1 2(х+1) = 9 2х+2=9 2х=7 х=3,5 Ответ: человек стоит на расстоянии 3,5 метров от столба
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Решение Найдем на сколько переместится 1 м: 2/0,5=4 м Значит 6 м опустятся на: 6/4=1.5 м Ответ: на 1,5 м
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
Решение Два подобных треугольника на чертеже — у большого в основании фонарь, у малого человек, вершина — конец тени. X — расстояние до фонаря. Составим пропорцию для подобных. 5/(x+9) = 1,8/9 1,8 (x+9) = 5*9 1,8x = 45 — 1,8*9 x=16м
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
Решение Х-высота столба х/1,6=(17+8)/8 х=1,6*25/8=5м
Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
S=сторона*высоту=АД*ВН АД=44+11=55 ВН найдем из Δ АВН Δ АВН- прямоугольный по теореме Пифагора ВН²=АВ²-АН² АН=44 по условию АВ=АД=55 (у ромба все стороны равны) ВН²=55²-44²=3025-1936=1089 ВН=√1089=33 S=55*33=1815
Человек, рост которого равен 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина тени человека равна 2 м. Определите высоту фонаря (в метрах).
Пусть х — высота фонаря 1)Рассмотрим треуг. ABC и треуг. BED: угол С = углу D => треугольники равны по первому признаку подобия угол B — общий 2) Значит 2/5=1.6/x 2x = 8 x = 4 Ответ: 4м
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо —6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Найдем на сколько переместится 1 м: 2/0,5=4 м Значит 6 м опустятся на: 6/4=1.5 м Ответ: на 1,5 м
В треугольнике ABC проведена биссектриса AL , угол ALC равен 112∘ , угол ABC равен 106∘ . Найдите угол ACB . Ответ дайте в градусах.
Угол ALB= 180∘-112∘=68∘ угол BAL=180-(68+106)=6∘ угол BAL= углу LAC = 6∘ угол ACB= 180-(112+6)=62∘
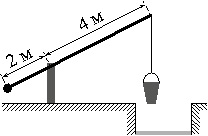
Задание 17. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Решение. По сути, в задаче нужно найти величину из двух подобных прямоугольных треугольников (по двум углам), показанных на рисунке ниже. Так как треугольники подобны, то можно записать соотношения для их сторон: откуда То есть конец длинного плеча опустится на 1 метр. Ответ: 1.
Задание 17. Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м? .
Решение. Ствол дерева представляет собой высоту, которая с землей составляет угол в 90 градусов, то есть на рисунке изображен прямоугольный треугольник, у которого известны два катета 1,2 м и 1,6 м, и нужно найти гипотенузу (длину лестницы). По теореме Пифагора, имеем: .
Задание 17. Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
Решение. Ствол дерева представляет собой высоту, которая с землей составляет угол в 90 градусов, то есть на рисунке изображен прямоугольный треугольник, у которого известны два катета 0,7 м и 2,4 м, и нужно найти гипотенузу (длину лестницы). По теореме Пифагора, имеем: . Ответ: 2,5.
Задание 17. Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,7 м, высота средней опоры 2,1 м. Найдите высоту большей опоры. Ответ дайте в метрах.
Решение. По сути, малая и большая опоры являются основаниями прямоугольной трапеции, а средняя опора – средней линией трапеции. Пусть длина большой опоры равна , тогда из формулы средней линии трапеции, имеем: Откуда Ответ: 2,5.
Задание 17. Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 2,2 м, высота большей опоры 2,5 м. Найдите высоту меньшей опоры. Ответ дайте в метрах.
Решение. Малая и большая опоры образуют основания прямоугольной трапеции, а среднюю опору можно воспринимать как среднюю линию трапеции. Известно, что средняя линия трапеции равна полусумме ее оснований. Обозначим через длину малой опоры, тогда можно записать равенство: откуда Ответ: 1,9.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 952 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 675 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 311 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 558 234 материала в базе
Другие материалы
- 15.01.2017
- 341
- 0
- 15.01.2017
- 587
- 0
- 15.01.2017
- 925
- 0
- 15.01.2017
- 456
- 1
- 15.01.2017
- 2310
- 3
- 15.01.2017
- 530
- 4
- 15.01.2017
- 485
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 15.01.2017 17273
- PPTX 1.7 мбайт
- 481 скачивание
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Гарипов Рафаэль Насихович. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет
- Подписчики: 1
- Всего просмотров: 66997
- Всего материалов: 41
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Петербургская учительница уволилась после чтения на уроке Введенского и Хармса
Время чтения: 3 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
В Рособрнадзоре рассказали, как будет меняться ЕГЭ
Время чтения: 2 минуты
У детей на портале госуслуг появятся собственные аккаунты
Время чтения: 1 минута
В «Единой России» предложили ввести раздел безопасности детей в интернете в курс ОБЖ
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
🔥 Видео
Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Подобные треугольникиСкачать

Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Задача на подобие треугольников 1частьСкачать

ОГЭ геометрия задача на подобие треугольников про тень от фонаряСкачать

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Геометрия . Задачи на подобие треугольников. Изи.Скачать

ОГЭ по математике. Задание 15. Все задачи на подобные треугольники.Скачать

ОГЭ математика. Задания 1-5 Земледельческие террасы. Ященко и решу ОГЭСкачать

Математика ОГЭ Геометрия, задача на подобие треугольниковСкачать
Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Задача 15 ОГЭ: подобные треугольники в трапецииСкачать

ОГЭ: задачи на подобие треугольниковСкачать

Сложная задача на подобие треугольников (видео 11)| Подобие. Геометрия | МатематикаСкачать

Полезные формулы из подобия треугольников. Задания 15 и 23/24 ОГЭСкачать

ОГЭ Задание 24 Первый признак подобия треугольниковСкачать