Задачи на остроугольные треугольники

Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.

Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.

Видео:Остроугольный треугольникСкачать

Виды, признаки и свойства остроугольных треугольников

Трехсторонние фигуры разделяются на множество подвидов и категорий.

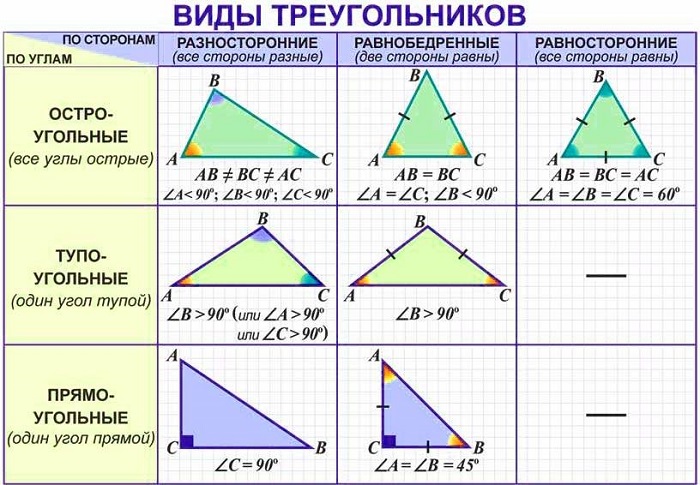
Общая классификация по наибольшему углу делит их на 3 группы:

Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.

3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;

сумма длин любых двух сторон больше оставшейся третьей.

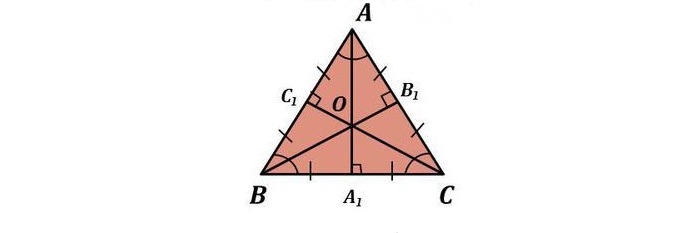
Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:

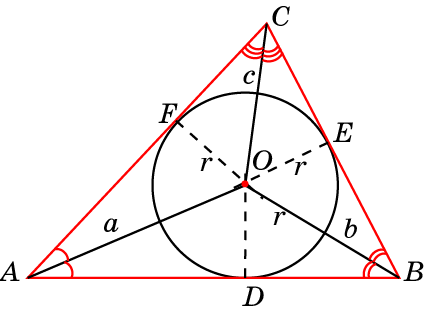
1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.

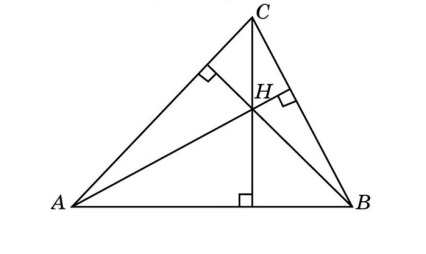
2. Высоты пересекаются в одной точке, образуя ортоцентр.

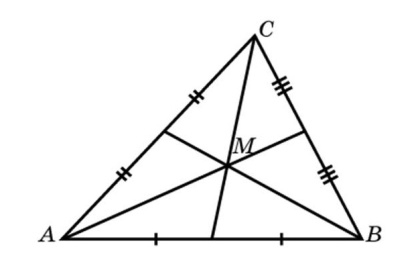
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).

Уникальные особенности зависят от разновидностей фигуры.

Видео:32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Равносторонний треугольник

«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.

Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Разносторонний треугольник

Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.

Уникальных отличий не имеет, только общие:

все параметры имеют разные значения;

совпадений между вспомогательными линиями нет.

Видео:Треугольники: остро-, тупо- и прямоугольныеСкачать

Равнобедренный остроугольный треугольник

Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.

проведенная к основанию линия – и биссектриса, и высота, и медиана;

вспомогательные линии из крайних точек при основании совпадают.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Равнобедренный тупоугольный треугольник

Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.

Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.

Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.

В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.

Видео:Треугольники. Практическая часть - решение задачи. 7 класс.Скачать

Что такое остроугольный треугольник

Остроугольным называется треугольник, у которого все углы меньше прямого.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Примеры решения задач

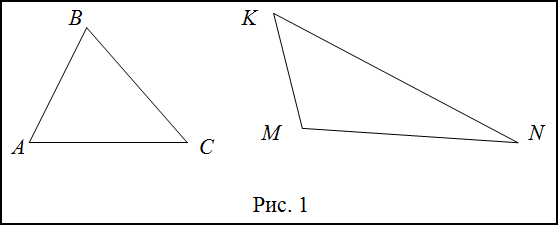
Задание. Определить какой из треугольников на рисунке 1 является остроугольным.

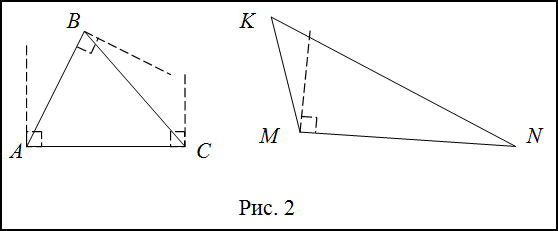
Решение. Сравним углы треугольников $ABC$ и $KMN$ с прямым углом. Для этого в каждой из вершин треугольника построим прямой угол.

В треугольнике $ABC$ как видно, все углы меньше прямого, следовательно, он остроугольный. В треугольнике $KMN$ $angle M$ больше, чем прямой угол, поэтому этот треугольник тупоугольный.

Ответ. $Delta A B C$ — остроугольный.

Задание. В треугольниках $ABC$ и $KMN$ известны два угла: $angle A=52^$, $angle C=42^$, $angle M=32^$, $angle N=22^$. Определить есть ли среди них остроугольный треугольник.

Решение. Найдем недостающие углы в треугольниках, для этого воспользуемся теоремой про сумму углов треугольника.

В треугольнике $ABC$:

Таким образом, в треугольнике $ABC$ все углы меньше $90^$, значит он остроугольный.

В треугольнике $KMN$:

Таким образом, в треугольнике $KMN$ угол $angle K$ больше $90^$, значит он тупоугольный.

Ответ. $ABC$ — остроугольный.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Задачи на остроугольные треугольники

Наглядная геометрия 7 класс. Ключевые задачи по теме Треугольники

Запомните!

1. Признаки равенства треугольников.

• 1-й. По двум сторонам и углу между ними.
• 2-й. По стороне и двум прилежащим к ней углам.
• 3-й. По трем сторонам.

2. Свойство углов равнобедренного треугольника.

Углы при основании равнобедренного треугольника равны.

3. Обратная теорема.

Если два угла треугольника равны, то треугольник равнобедренный.

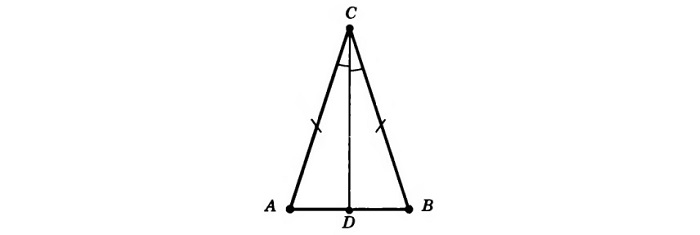
4. Свойство биссектрисы равнобедренного треугольника.

Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают.

5. Признаки равнобедренного треугольника. Треугольник является равнобедренным, если:

• а) высота является и медианой;
• б) высота является и биссектрисой;
• в) биссектриса является и медианой.

6. Теорема о свойстве точек серединного перпендикуляра.

• Любая точка серединного перпендикуляра равноудалена от концов отрезка.
• Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.

7. Теорема о пересечении серединных перпендикуляров.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной около треугольника окружности.

Простые вопросы по теме «Треугольники»

1. В треугольнике провели медиану. Сколько треугольников изображено на рисунке?
2. Если стороны треугольника продлить, то сколько углов всего образуется, не считая развернутых? А считая и развернутые?
3. Верно ли, что биссектриса треугольника лежит на биссектрисе угла?
4. Может ли высота треугольника делить сторону пополам?
5. Может ли биссектриса треугольника быть перпендикулярной стороне треугольника?
6. Верно ли утверждение: «Биссектриса равнобедренного треугольника является высотой и медианой»?
7. Является ли любой равнобедренный треугольник равносторонним?
8. Является ли любой равносторонний треугольник равнобедренным?
9. Может ли биссектриса некоторого равнобедренного треугольника, проведенная к боковой стороне, быть медианой?
10. Может ли высота треугольника быть равна его медиане, проведенной из той же вершины?
11. Может ли биссектриса треугольника быть равна его высоте, проведенной из той же вершины?
12. Существует ли треугольник, периметр которого в 3 раза больше одной из сторон?
13. Если медиана образует равные углы с соседними сторонами треугольника, то какой угол она образует с третьей стороной?
14. Что для студентов означает слово «медиум»?
15. Сколько всего теорем в данной теме?

Непростые вопросы по теме «Треугольники»

16* В треугольнике провели 2 медианы. Сколько треугольников изображено на рисунке?
17* В треугольнике провели 3 медианы. Сколько треугольников изображено на рисунке?
18* Может ли в треугольнике высота являться медианой, но не являться биссектрисой?
19* Как звучит теорема о свойстве углов равнобедренного треугольника в форме «Если …, то …»?
20* Как звучит утверждение, обратное теореме о свойстве углов равнобедренного треугольника, в форме «Если …, то …»?
21* Может ли медиана треугольника равняться соседней стороне?
22* Может ли биссектриса треугольника равняться соседней стороне?
23* Может ли высота треугольника равняться соседней стороне?
24* Может ли серединный перпендикуляр к стороне треугольника иметь общую точку с каждой из двух других сторон?
25* Может ли серединный перпендикуляр к стороне треугольника делить противоположный угол треугольника пополам?

Ответы на простые и непростые вопросы

1. Три. Два маленьких и один данный.
2. 12; 24.
3. Да.
4. Да. В равнобедренном треугольнике.
5. Да. В равнобедренном треугольнике.
6. Нет. Только биссектриса, проведенная из вершины к основанию.
7. Нет.
8. Да.
9. Да. Если треугольник равносторонний.
10. Да. В равнобедренном треугольнике это высота, проведенная к его основанию.
11. Да. В равнобедренном треугольнике это биссектриса, проведенная к его основанию.
12. Да. Например, равносторонний.
13. 90°. Если медиана является биссектрисой, то треугольник равнобедренный и эта медиана является и высотой, проведенной к основанию.
14. Медиум — студенческий праздник, знаменующий середину учебы.
15. Тринадцать теорем, включая задачу о пересечении серединных перпендикуляров к сторонам треугольника.

16* 8.
17* 16.
18* Нет. Если высота является медианой, то треугольник равнобедренный и эта высота является и биссектрисой.
19* «Если треугольник равнобедренный, то углы при основании равны». 20* «Если у треугольника два угла равны, то треугольник равнобедренный».
21* Да.
22* Да.
23* Да. В прямоугольном треугольнике.
24* Да. В равнобедренном прямоугольном треугольнике.
25* Да. Если треугольник равнобедренный.

Это конспект по геометрии «Ключевые задачи по теме Треугольники». Выберите дальнейшие действия:

🎥 Видео

Как за 5 секунд решать такие задачи с треугольникиСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

№16 из ЕГЭ2022 и олимпиады. Красивое доказательство свойства ортоцентра остроугольного треугольникаСкачать

Площадь равностороннего, прямоугольного, тупо- и остроугольного треугольников. Решение задач 9 классСкачать

Остроугольные треугольникиСкачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Задача, которую боятсяСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

№267. Докажите, что два остроугольных треугольника равны, если сторона и высоты, проведенные изСкачать

Остроугольный , тупоугольный и прямоугольный треугольники | Геометрия 7-9 класс #32 | ИнфоурокСкачать

Задача ФаньяноСкачать