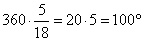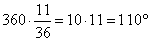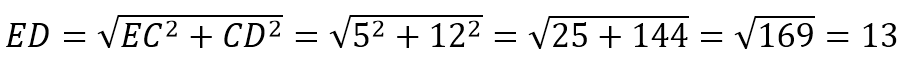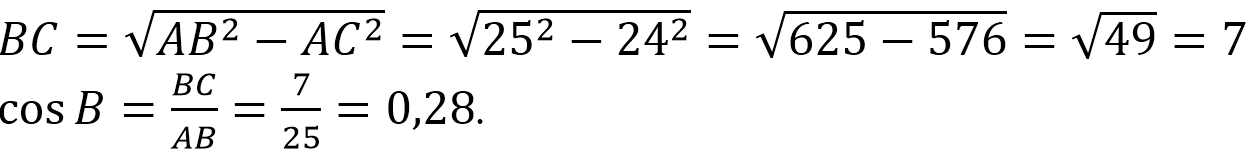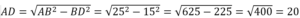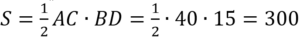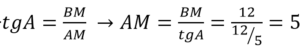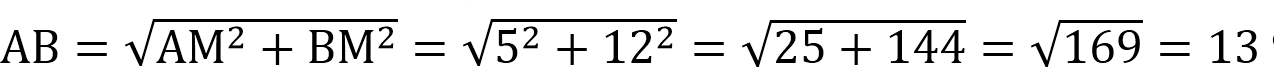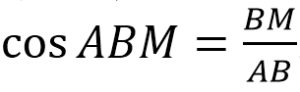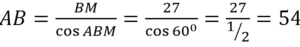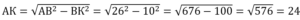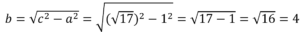Задачи егэ площадь треугольника

Тренажер задания 3 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 3 — задачи на площади треугольников, параллелограмма, ромба, трапеции и прямоугольника. Это задание на планиметрию. Номер заданий соответствует номеру заданий в базе mathege.ru.

Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Площадь треугольника

27617. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

27623. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

27589. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30º. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

27590. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150º. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.

27591. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30º.

27620. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30º. Найдите боковую сторону треугольника, если его площадь равна 25.

27621. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150º. Найдите боковую сторону треугольника, если его площадь равна 10.

27619. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.

27592. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.

27618. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

27624. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Параллелограмм

27610. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

27611. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

27612. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

319056. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма.

319057. Площадь параллелограмма ABCD равна 176. Точка E – середина стороны CD. Найдите площадь треугольника ADE.

Видео:Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать

Ромб

27613. Найдите площадь ромба, если его высота равна 2, а острый угол 30º.

27614. Найдите площадь ромба, если его диагонали равны 4 и 12.

27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.

27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Прямоугольник

27605. Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.

27582. Найдите площадь квадрата, если его диагональ равна 1.

Видео:ЕГЭ по математике | профиль - Задание 1 (Задачи на площадь треугольника)Скачать

Трапеция

27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150º. Найдите площадь трапеции.

27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

27636. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45º.

27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

317338. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.

319058. Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABDE.

27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Задание №15 ЕГЭ по математике базового уровня

Видео:ПЛОЩАДЬ ТРЕУГОЛЬНИКА егэ по математикеСкачать

Планиметрия

В задании № 15 базового уровня ЕГЭ по математике нас ждет решение задач по планиметрии. Задачи в этом разделе не сложные, достаточно знать определения основных понятий и базовые формулы, после чего задача сводится к элементарным вычислениям.

Разбор типовых вариантов заданий №15 ЕГЭ по математике базового уровня

Вариант 15МБ1

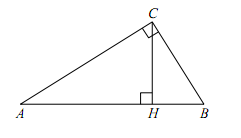
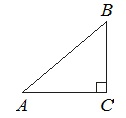
В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.

Алгоритм выполнения:

1. Вспомнить определение косинуса угла.
2. Записать выражение для нахождения косинуса угла.
3. Выразить неизвестную величину.
4. Вычислить.

Решение:

Вспомним определение косинуса угла.

Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.

Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH.

Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза.

Прилежащий к углу А катет – АН.

Получим cos A = АН/АС.

Выразим неизвестную величину.

АН = АС · cos A = 4 · 0,8 = 3,2

Вариант 15МБ2

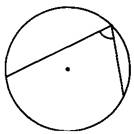
Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

1. Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
2. Вычислить градусную меру угла, на который опирается дуга.
3. Вычислить вписанный угол.

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 5/18 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ3

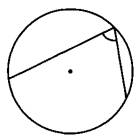
Найдите вписанный угол, опирающийся на дугу, длина которой равна 11/36 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

1. Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
2. Вычислить градусную меру угла, на который опирается дуга.
3. Вычислить вписанный угол.

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 11/36 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ4

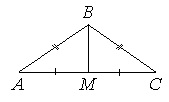
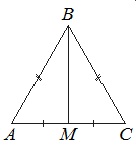
В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ.

Алгоритм выполнения

1. Определяем

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Решение:

Если АВ=ВС, то ∆АВС – равнобедренный.

В равнобедр.треугольнике медиана, опущенная на основание, является еще и высотой. Тогда угол АМВ=90 0 , и ∆АМВ – прямоугольный с катетами АМ и ВМ и гипотенузой АВ.

По т.Пифагора АМ 2 +ВМ 2 =АВ 2 . Отсюда: .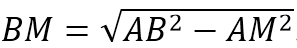

Т.к. АМ медиана, то

.

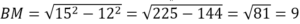
Вариант 15МБ5

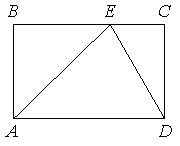
На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.

Алгоритм выполнения

1. Находим ЕС.
2. Определяем значение СD.
3. Из прямоугольного треугольника АСD по т.Пифагора находим ЕD.

Решение:

Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.

Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.

Рассмотрим ∆ЕСD. Т.к. АВСD прямоугольник, то угол С=90 0 , и ∆ЕСD прямоугольный.

Тогда по т.Пифагора ЕD 2 =ЕC 2 +СD 2 . Получаем:

Вариант 15МБ6

В треугольнике АВС угол С равен 90 0 , АВ=25, АС=24. Найдите cos B.

Алгоритм выполнения

1. По т.Пифагора находим величину катета ВС.
2. По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе.

Решение:

Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ 2 =АС 2 +ВС 2 .

Вариант 15МБ7

В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.

Алгоритм выполнения

1. Из вершины В

Проводимость — способность живой ткани проводить возбуждение.

Решение

В ∆ADB угол А является противолежащим к BD. Поэтому sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.

Из ∆ADB по т.Пифагора имеем: AB 2 =AD 2 +BD 2 →

Т.к. ∆АВС равнобедренный, то высота BD, проведенная к основанию, является и медианой. Поэтому АС=2АD=2·20=40.

Площадь ∆АВС равна:

Вариант 15МБ8

В равнобедренном треугольнике АВС медиана ВМ, проведенная к основанию, равна 12, а tg А=12/5. Найдите длину боковой стороны треугольника АВС.

Алгоритм выполнения

1. Доказываем, что ∆АВМ прямоугольный.
2. Из ∆АВМ, используя формулу-определение для тангенса, находим АМ.
3. Из ∆АВМ по теореме Пифагора находим АВ.

Решение:

Т.к. ∆АВС равнобедренный, то медиана ВМ, проведенная к основанию, является и высотой. Тогда ∆АВМ прямоугольный.

Из ∆АВМ по теореме Пифагора АВ 2 =АМ 2 +ВМ 2 →

Вариант 15МБ9

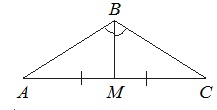
В треугольнике АВС угол В равен 120 0 . Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ.

Алгоритм выполнения

1. Определяем величину угла АВМ.
2. Доказываем, что ∆АМВ прямоугольный.
3. Находим АВ, используя формулу-определение для косинуса.

Решение:

По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет

Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.

В прямоугольного ∆АМВ:

Вариант 15МБ10

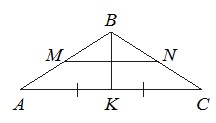
В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.

Алгоритм выполнения

1. Доказываем, что ∆АКВ прямоугольный.
2. Из ∆АКВ по т.Пифагора находим АК.
3. Находим АС как 2АК.
4. Находим МN как среднюю линию.

Решение:

Т.к. ∆АВС равнобедренный, то медиана ВК, опущенная на основание АС, является и высотой. Поэтому угол АКВ равен 90 0 , и ∆АКВ прямоугольный.

Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 .

Поскольку ВК медиана, то АС=2АК=2·24=48.

Линия, соединяющая в треугольники середины двух сторон, называется средней линией. Ее величина составляет половину третьей стороны (которой она параллельна).

Вариант 15МБ11

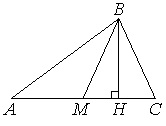
В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.

Алгоритм выполнения

1. Находим длину отрезков АМ и МС как половину от АС.
2. Доказываем, что ВН является медианой в ∆МВС. Отсюда определяем, что МН – половина от МС.
3. Находим АН как сумму АМ и МН.

Решение:

Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.

По условию ВС=ВМ, поэтому ∆МВС равнобедренный с основанием МС и равными боковыми сторонами ВМ и ВС. Тогда высота, проведенная к основанию, является еще и медианой. Отсюда следует, что МН=НС=МС/2=28/2=14.

Вариант 15МБ12

Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17, а один из катетов равен 1.

Алгоритм выполнения

1. Находим величину 2-го (неизвестного) катета по т.Пифагора.
2. Определяем площадь треугольника как полупроизведение катетов.

Решение:

Обозначим 1-й (известный) катет через а, 2-й – через b, гипотенузу – через с.

По т.Пифагора a 2 +b 2 =c 2 . Отсюда:

Т.к. треугольник прямоугольный, то его площадь можно найти по ф-ле: S=a·b/2. Тогда: S=1·4/2=2.

Вариант 15МБ13

В равнобедренном треугольнике АВС основание АС равно 32, площадь треугольника равна 192. Найдите длину боковой стороны АВ.

Алгоритм выполнения

1. Используя формулу для площади треугольника S=ah/2 и зная величину а (по условию – основание АС), найдем высоту ∆АВС. Отображаем высоту на рисунке, обозначив ее пересечение с основанием буквой К.
2. Доказываем, что высота ВК является и его медианой. Отсюда находим АК.
3. Из ∆АКВ по т.Пифагора находим АВ.

Решение:

Площадь треугольника определяется по ф-ле: S=ah/2, где а=АС=32. Отсюда находим высоту ВК: BK=h=2S/a → ВК=2·192/32=12.

Т.к. ∆АВС равнобедренный, то высота, опущенная в нем на основание, является и медианой. Тогда АК=АС/2=32/2=16.

Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 . Получаем:

Видео:Лайфхак! Площади всех фигур #огэ #математика #shortsСкачать

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

💥 Видео

Задача из ОГЭ на площадь треугольника #математика #огэматематика #огэ #семенСкачать

ЗАДАНИЕ 1|ЕГЭ ПРОФИЛЬ| Площадь треугольника ABC равна 52, DE-средняя линия, параллельная стороне AB.Скачать

Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

Площадь по теореме Герона #математика #площадь #треугольник #герона #егэ #огэ #найтиплощадь #теоремаСкачать

Планиметрия с нуля и до уровня ЕГЭ 2023 за 4 часа | Вся теория по №1,16 | Математика профильСкачать

Вариант #20 из задач ФИПИ - Уровень Сложности ЕГЭ 2024| Математика Профиль| Оформление на 100 БалловСкачать

Задача 6 №27591 ЕГЭ по математике. Урок 59Скачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

КАК ЗАПОМНИТЬ ОБЪЕМЫ ВСЕХ ФИГУР? #shorts #математика #егэ #огэ #профильныйегэСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Площади фигур. Повторяем формулы и решаем задачи. Вебинар | МатематикаСкачать