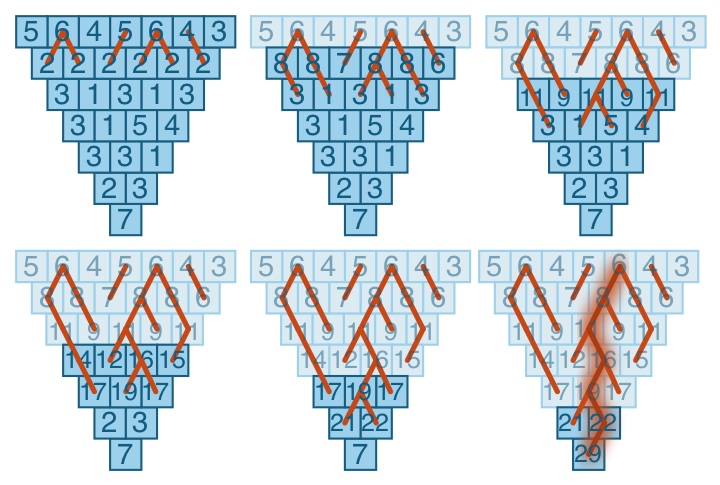Задача о треугольнике динамическое программирование

Видео:Динамическое программирование — это просто | Скринкасты | Академия данных MADE | #1Скачать

1. Идея метода динамического программирования

Динамическое программирование является одним из методов решения задач, в которых задачу большой размерности можно решать, опираясь на уже решенные задачи меньшего размера.

Словосочетание «динамическое программирование» впервые было использовано в 1940-х годах Р. Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей.

Динамическое программирование может быть применено при выполнении следующих условий:

1) Существует способ выразить решение задачи через решение подзадач меньшей размерности. Этот способ задается рекуррентными соотношениями.

2) Существуют известные решения для задачи малой размерности (задача малой размерности решается просто).

Динамическое программирование вычисляет решение для всех подзадач. Вычисление идет от малых подзадач к большим. Решения подзадач запоминаются в таблице. Мы заполняем эту таблицу независимо от того, нужна ли нам на самом деле конкретная подзадача для получения общего решения.

Преимущество метода состоит в том, что раз уж задача решена, ее ответ хранится и никогда не вычисляется заново.

Можно выделить два класса задач, решаемых методом динамического программирования.

Задачи из первого класса связаны с вычислением сумм или произведений в зависимости от постановки задачи.

Ко второму классу относятся оптимизационные задачи, для которых может быть сформулирован принцип оптимальности; суть принципа оптимальности состоит в том, что решения подзадач, используемые для нахождения оптимального решения задачи, также должны быть оптимальными.

Мы рассмотрим на примерах использование метода динамического программирования для задач из обоих классов.

Видео:Задача о рюкзаке. Динамическое программирование.Скачать

2. Рекуррентные соотношения

Приведем два примера задач, для которых можно записать такие рекуррентные соотношения.

Задача о числах Фибоначчи.

Задача состоит в вычислении N-ого числа в последовательности Фибоначчи 0, 1, 2, 3, 5, 8, . , в которой первое число равно нулю, второе равно единице, а все остальные представляют собой сумму двух предыдущих чисел.

Обозначим F_i число Фибоначчи, стоящее на i-м месте в последовательности (считаем 0 нулевым членом последовательности). Последовательность чисел Фибоначчи определяется рекуррентным соотношением

Задача о числе сочетаний.

Для n-элементного множества сочетанием из n элементов по k называется произвольное подмножество из k элементов. Например, для множества B=<a,b,c,d> его подмножество <b,d> – это сочетание из 4-х элементов по 2.

Обозначение применяется для числа всех сочетаний из n элементов по k. Так, для множества B множество всех двухэлементных подмножеств равно <<a,b>, <a,c>, <a,d>, <b,c>, <b,d>, <c,d>> и, следовательно,

Величины называются также биномиальными коэффициентами.

Известно рекуррентное соотношение для вычисления :

позволяющее вычислять значение по значениям для числа сочетаний при меньших значениях параметров n и k.

Заметим, что – быстро растущая функция, поэтому для вычислений по этой формуле нужна арифметика «больших чисел».

Видео:Задача из Собеседования в Google на Динамическое Программирование: Количество Уникальных ПутейСкачать

3. Динамическое программирование в задачах на поиск суммы

3.1. Числа Фибоначчи

Формула (1) задает рекуррентное соотношение для чисел Фибоначчи, позволяющее решать задачу нахождения n-го числа Фибоначчи методом динамического программирования.

Вычисление начинается с задания значений для первых двух чисел Фибоначчи: F₀ =0, F₁ =1. Таким образом, нам известны решения для самых маленьких подзадач. Далее по F₀ и F₁ мы вычисляем F₂ , складывая F₀ и F₁, и запоминаем в таблице, по F₁ и F₂ находим F₃ и его значение запоминаем в таблице, и т.д., до тех пор, пока не найдем n-е число Фибоначчи.

Для хранения вычисляемых чисел Фибоначчи будем использовать одномерный массив F; элемент F[i] содержит значение F_i.

Алгоритм на псевдокоде выглядит так:

begin

for i = 2 to n do F[i] = F[i-1]+F[i-2]

end

Число ячеек используемой памяти для вычисления F_n имеет порядок n. Поскольку время вычислений пропорционально числу используемых ячеек массива F, трудоемкость алгоритма оценивается как O(n).

Объем используемой памяти можно сократить, если заметить, что для вычисления очередного числа Фибоначчи используются только два предыдущих значения. Поэтому достаточно трех ячеек для запоминания чисел из последовательности Фибоначчи.

3.2. Треугольник Паскаля

Из формулы (2) вытекает эффективный способ рекуррентного вычисления значений биномиальных коэффициентов, который можно представить в графической форме, известной как треугольник Паскаля.

В этом равнобедренном треугольнике каждое число (кроме единиц на боковых сторонах) является суммой двух чисел, стоящих над ним. Число сочетаний находится в (n+1)-м ряду на (k+1)-м месте.

1

1

1

1

2

1

1

3

3

1

1

4

6

4

1

Рис. 1. Треугольник Паскаля

Чтобы найти значение , достаточно последовательно заполнить таблицу по строкам для n = 1, 2, … , пока не дойдем до нужных значений n и k.

Приведем описание на псевдокоде алгоритма вычисления числа сочетаний, в основе которого лежит метод динамического программирования. Алгоритм использует двумерный массив D, для элемента D[i, j] индекс i соответствует номеру строки таблицы в треугольнике Паскаля, индекс j – номеру столбца.

procedure БИНОМ_КОЭФ(n,k)

begin

for i=3 to n+1 do

begin

for j=2 to i-1 do

end

end

Таблица для треугольника Паскаля занимает O(n 2 ) ячеек памяти, но можно сократить ее до O(n), заметив, что для вычисления следующей строки нужна только предыдущая. Время работы алгоритма пропорционально числу заполненных клеток таблицы и имеет порядок n 2 .

Применение метода динамического программирования позволяет во многих случаях улучшить трудоемкость алгоритма за счет сокращения дублирования вычислений. К примеру, для вычисления используются ранее вычисленные значения и , для вычисления которых в свою очередь используется значение . Если бы мы не хранили в таблице результаты всех предыдущих вычислений, пришлось бы вычислять дважды.

Заметим, что уменьшение вычислительной сложности алгоритма достигается за счет увеличения объема используемой памяти.

Видео:Динамическое программирование: траектории кузнечикаСкачать

4. Динамическое программирование в оптимизационных задачах. Перекрытие подзадач

Метод динамического программирования может применяться для комбинаторных задач, в которых требуется найти оптимальное решение, то есть решение, дающее минимум (или максимум) некоторой целевой функции. Динамическое программирование применяется к решению таких задач, для которых может быть сформулирован принцип оптимальности, заключающийся в следующем:

Частичные решения, т.е. решения подзадач, из которых получается решение всей задачи, являются оптимальными решениями этих подзадач.

Применение принципа оптимальности к решению комбинаторных задач по существу означает использование принципа декомпозиции: вначале находятся оптимальные решения подзадач малого размера, затем они используются для отыскания оптимальных решений бóльших подзадач и, наконец, для решения самой задачи.

Второе свойство задач, необходимое для использования динамического программирования – малость множества подзадач. Благодаря этому при рекурсивном решении задачи мы все время выходим на одни и те же подзадачи. В таком случае говорят, что у оптимизационной задачи имеются перекрывающиеся подзадачи. В типичных случаях количество подзадач полиномиально зависит от размера исходных данных.

Алгоритмы, основанные на динамическом программировании, используют перекрытие подзадач следующим образом: каждая из подзадач решается только один раз, и ответ заносится в специальную таблицу; когда эта же подзадача встречается снова, программа не тратит время на ее решение, а берет готовый ответ из таблицы.

Продемонстрируем использование метода динамического программирования на примере задачи триангуляции выпуклого многоугольника.

4.1. Оптимальная триангуляция многоугольника

Прежде чем сформулировать задачу, введем некоторые определения.

Многоугольник – это замкнутая кривая на плоскости, составленная из отрезков, называемых сторонами многоугольника. Многоугольник называется выпуклым, если для любых двух точек, лежащих внутри или на границе многоугольника, соединяющий их отрезок целиком лежит внутри или на границе многоугольника. Диагональ многоугольника – это отрезок, соединяющий две вершины, не являющиеся соседними.

Выпуклый многоугольник можно задать, перечислив его вершины в порядке обхода по часовой стрелке. Будем считать, что многоугольник имеет n вершин v₁, v₂, … , v_n, заданных своими координатами на плоскости.

Под триангуляцией будем понимать набор непересекающихся диагоналей, которые разбивают многоугольник на треугольники. Триангуляцию можно также определить как наибольшее множество непересекающихся диагоналей.

Многоугольник может иметь несколько различных триангуляций, но все они состоят из n-3 диагоналей и разбивают многоугольник на n-2 треугольника. Примеры триангуляций семиугольника приведены на рис. 2.

Стоимость триангуляции определим как сумму длин диагоналей.

Задача о триангуляции многоугольника состоит в нахождении триангуляции с наименьшей стоимостью.

Видео:Лекция 4. Динамическое программирование 1Скачать

Максимальная сумма пути в треугольнике.

Мы дали числа в форме треугольника, начав с вершины треугольника и перейдя к соседним числам в строке ниже, чтобы найти максимальную сумму сверху вниз.

Примеры :

Мы можем пройти через грубую силу, проверив все возможные пути, но это занимает много времени, поэтому мы должны попытаться решить эту проблему с помощью динамического программирования, которое уменьшает сложность времени.
Если нам нужно сдвинуть влево каждый элемент и поставить 0 в каждой пустой позиции, чтобы сделать его регулярной матрицей, то наша задача выглядит как путь с минимальными затратами.
Итак, после преобразования наших входных треугольных элементов в регулярную матрицу мы должны применить динамическую программную концепцию, чтобы найти максимальную сумму пути.
Применяя DP снизу вверх, мы должны решить нашу проблему следующим образом:
Пример:

// C ++ программа для Dynamic
// Программирование реализации
// Задача максимальной суммы в треугольнике
#include

using namespace std;

// Функция для поиска максимальной суммы

int maxPathSum( int tri[][N], int m, int n)

// цикл для восходящего расчета

for ( int i=m-1; i>=0; i—)

// для каждого элемента проверяем оба

// элементы чуть ниже числа

// и ниже справа от номера

// добавляем максимум к нему

if (tri[i+1][j] > tri[i+1][j+1])

// вернуть верхний элемент

// который хранит максимальную сумму

/ * Программа драйвера для проверки вышеуказанных функций * /

// Java-программа для Dynamic
// Программирование реализации
// Задача максимальной суммы в треугольнике

static int N = 3 ;

// Функция для поиска максимальной суммы

static int maxPathSum( int tri[][], int m, int n)

// цикл для восходящего расчета

for ( int i = m — 1 ; i >= 0 ; i—)

for ( int j = 0 ; j

// для каждого элемента проверяем оба

// элементы чуть ниже числа

// и ниже справа от номера

// добавляем максимум к нему

if (tri[i + 1 ][j] > tri[i + 1 ][j + 1 ])

tri[i][j] += tri[i + 1 ][j];

tri[i][j] += tri[i + 1 ][j + 1 ];

// вернуть верхний элемент

// который хранит максимальную сумму

return tri[ 0 ][ 0 ];

/ * Программа драйвера для проверки вышеуказанных функций * /

public static void main (String[] args)

System.out.println ( maxPathSum(tri, 2 , 2 ));

// Этот код предоставлен vt_m

# Python программа для
# Динамическое программирование
# реализация Макс
# сумма проблем в
# треугольник

# Функция для поиска максимальной суммы

def maxPathSum(tri, m, n):

# цикл для восходящего расчета

for i in range (m — 1 , — 1 , — 1 ):

for j in range (i + 1 ):

# для каждого элемента отметьте оба

# элементы чуть ниже числа

# и ниже справа от номера

# добавить максимум к нему

if (tri[i + 1 ][j] > tri[i + 1 ][j + 1 ]):

tri[i][j] + = tri[i + 1 ][j]

tri[i][j] + = tri[i + 1 ][j + 1 ]

# вернуть верхний элемент

# где хранится максимальная сумма

return tri[ 0 ][ 0 ]

# Программа драйвера для проверки вышеуказанной функции

print (maxPathSum(tri, 2 , 2 ))

# Этот код добавлен
# Сумен Гош.

// C # Программа для динамического программирования
// реализация задачи максимальной суммы
// в треугольнике

// Функция для поиска максимальной суммы

static int maxPathSum( int [,]tri,

// цикл для восходящего расчета

for ( int i = m — 1; i >= 0; i—)

for ( int j = 0; j

// для каждого элемента,

// проверяем оба элемента

// чуть ниже числа

// максимум их к этому

// вернуть верхний элемент

// который хранит максимальную сумму

/ * Программа драйвера для тестирования выше

public static void Main ()

maxPathSum(tri, 2, 2));

// Этот код предоставлен нитин митталь.

// PHP программа для Dynamic
// Программирование реализации
// Задача максимальной суммы в треугольнике

// Функция для поиска
// максимальная сумма

function maxPathSum( $tri , $m , $n )

// цикл снизу вверх

for ( $i = $m — 1; $i >= 0; $i —)

for ( $j = 0; $j $i ; $j ++)

// для каждого элемента проверяем

// оба элемента чуть ниже

// номер и справа внизу

// к числу добавляем максимум

if ( $tri [ $i + 1][ $j ] > $tri [ $i + 1]

$tri [ $i ][ $j ] += $tri [ $i + 1][ $j ];

$tri [ $i ][ $j ] += $tri [ $i + 1]

// вернуть верхний элемент

// который хранит максимальную сумму

$tri = array ( array (1, 0, 0),

echo maxPathSum( $tri , 2, 2);

// Этот код предоставлен ajit
?>

Выход :

Эта статья предоставлена Шивам Прадхан (anuj_charm) . Если вы как GeeksforGeeks и хотели бы внести свой вклад, вы также можете написать статью с помощью contribute.geeksforgeeks.org или по почте статьи contribute@geeksforgeeks.org. Смотрите свою статью, появляющуюся на главной странице GeeksforGeeks, и помогите другим вундеркиндам.

Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.

Видео:12 Задача о рюкзакеСкачать

Золотая пирамида — задача про треугольник, составленный из чисел

В этом выпуске рассмотрим классическую задачу, известную под названием «Золотая гора». На CheckiO её реализовали в этой задаче.

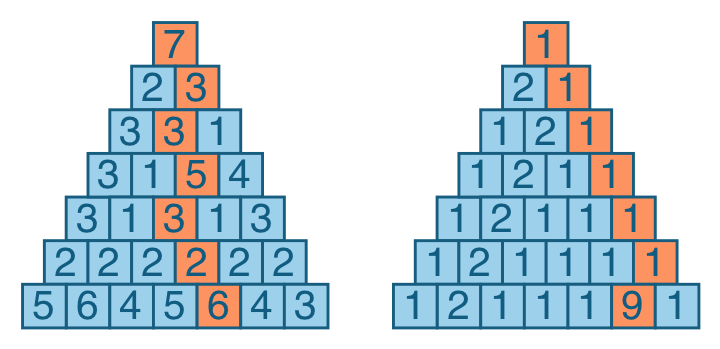
Представьте себе треугольник, составленный из чисел. Одно число расположено в вершине. Ниже размещено два числа, затем три, и так до нижней грани. Вы начинаете на вершине, и нужно спуститься к основанию треугольника. За каждый ход вы можете спуститься на один уровень и выбрать между двумя числами под текущей позицией. По ходу движения вы «собираете» и суммируете числа, которые проходите. Ваша цель — найти максимальную сумму, которую можно получить из различных маршрутов.

Рассмотрим различные методы решения.

Рекурсия

Первым делом в голову приходит мысль использовать рекурсию и просчитать все пути от вершины. Когда мы спускаемся на один уровень, то все доступные числа ниже образуют новый меньший треугольник, и можно запустить нашу функцию уже для нового подмножества и так пока не достигнем основания.

Как мы видим, на первом уровне мы запустим нашу функцию два раза, затем 4, 8, 16 раз и так далее. В итоге мы получим сложность алгоритма 2 N и, например, для 100-уровневой пирамиды нам нужно будет уже где-то ≈10 30 вызовов функции. Многовато.

Динамическое программирование

Что если попробовать использовать принцип динамического программирования и разбить нашу проблему на множество мелких подзадач, результаты которых мы затем аккумулируем. Попробуйте взглянуть на треугольник вверх ногами. А теперь на второй уровень (то есть предпоследний от основания). Для каждой ячейки мы можем решить, каким будет лучший выбор в наших маленьких трёхэлементных треугольничках. Выбираем лучший, суммируем с рассматриваемой ячейкой и записываем результат. Таким образом, мы получили наш треугольник, но на один уровень ниже. Повторяем данную операцию снова и снова. В результате нам нужно (N-1)+(N-2)+…2+1 операций и сложность алгоритма равна N 2 .

Решения игроков CheckiO

Пользователь gyahun_dash написал интересную реализацию описанного выше метода ДП в своем решении «DP». Он использовал reduce, чтобы проходить по парам строк, и map чтобы обработать каждую из них.

Игрок evoynov использовал двоичные числа, чтобы перебрать все возможные маршруты, представленные как последовательность 1 и 0 в своем решении «Binaries». И это наглядный пример сложности алгоритма с рекурсией и перебором всех маршрутов.

И чтобы не было скучно, посмотрим на легкий мозгодробитель от пользователя nickie и его однострочник «Functional DP», который только формально состоит из двух строк. Конечно, это решение из категории «Творческих» («Creative»). Не думаю, что автор использует такое на боевом коде. А просто для так для веселья, почему бы и нет.

Вот и всё на сегодня. Делитесь вашими идеями и мыслями.

Спасибо CheckiO за интересную задачу.

📹 Видео

Java. Задача о рюкзаке. Динамическое программирование.Скачать

План решения задачи методом динамического программирования. Центр онлайн-обучения «Фоксфорд»Скачать

Как решить задачу про банкомат методом динамического программированияСкачать

Динамическое программирование 1Скачать

Leetcode 322. Coin Change | Динамическое программированиеСкачать

Тренировки по алгоритмам 3.0. Лекция 3: «Динамическое программирование с одним параметром»Скачать

Динамическое программирование. Часть 4. Задача о рюкзаке. Knapsack problem. Код на PythonСкачать

Спортивное программирование 9М. Динамическое программирование. Треугольник ПаскаляСкачать

АиСД 1.7.1. Динамическое программирование. Основные принципы. Задача о кузнечике.Скачать

АиСД S01E10. Динамическое программированиеСкачать

Динамическое программирование. Часть 1. Одномерная динамика. Код на PythonСкачать

Задача из Собеседования на 160,000 Евро в ГодСкачать

АиСД S01E12. Задача о рюкзакеСкачать