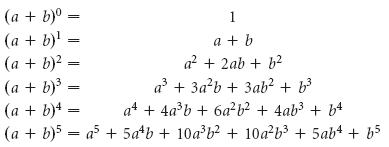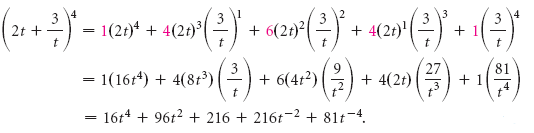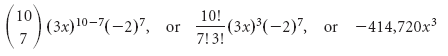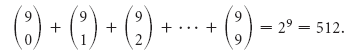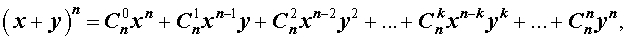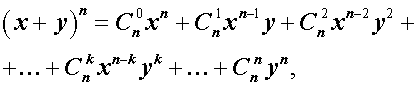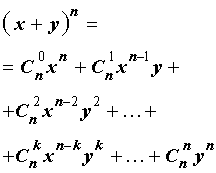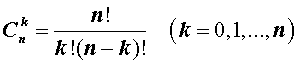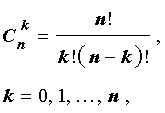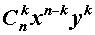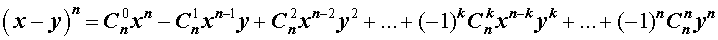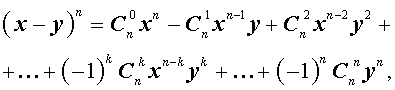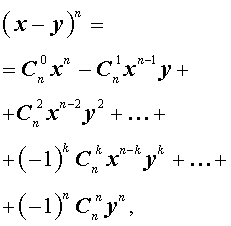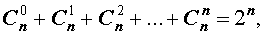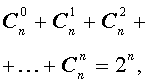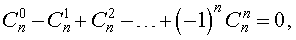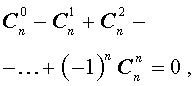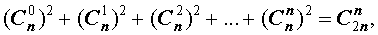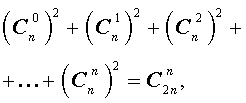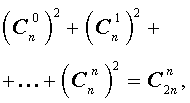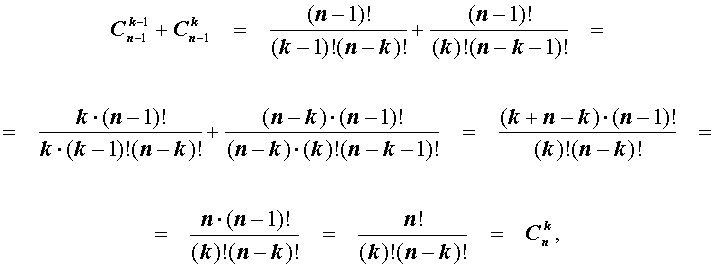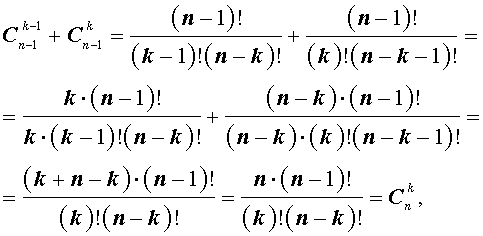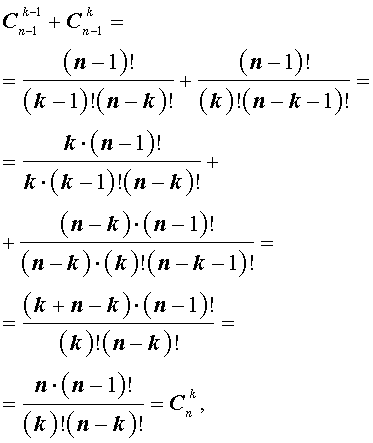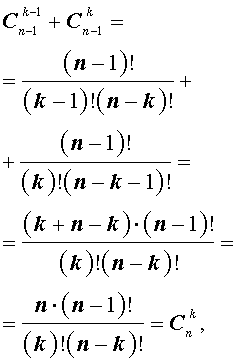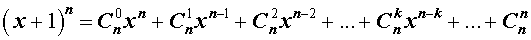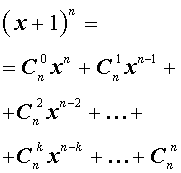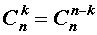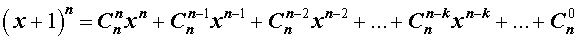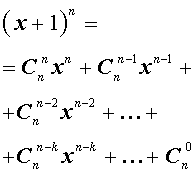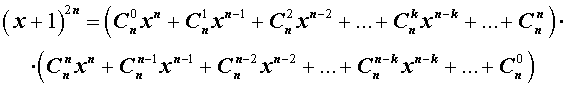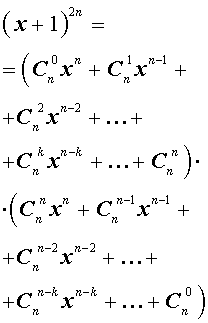- Биноминальное разложение с использованием треугольника Паскаля
- Бином Ньютона с использованием треугольника Паскаля
- Разложение бинома используя значения факториала
- Бином Ньютона с использованием обозначение факториала
- Нахождение определенного члена
- Нахождение (k + 1) члена
- Общее число подмножеств
- Полное число подмножеств
- Практическое занятие по теме: «Треугольник Паскаля. Бином Ньютона»
- Бином Ньютона
- Формула бинома Ньютона
- Связь бинома Ньютона с треугольником Паскаля
- Свойства биномиальных коэффициентов
- 🔥 Видео
Биноминальное разложение с использованием треугольника Паскаля
Рассмотрим следующие выражения со степенями (a + b) n , где a + b есть любой бином, а n — целое число.
Каждое выражение — это полином. Во всех выражениях можно заметить особенности.
1. В каждом выражении на одно слагаемое больше, чем показатель степени n.
2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.
3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.
4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до «половины пути», а потом уменьшаются на те же значения обратно к 1.
Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти значение (a + b) 6 . Согласно особенности, которую мы только что заметили, здесь должно быть 7 членов
a 6 + c1a 5 b + c2a 4 b 2 + c3a 3 b 3 + c4a 2 b 4 + c5ab 5 + b 6 .
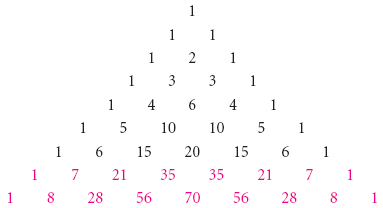
Но как мы можем определить значение каждого коэффициента, ci? Мы можем сделать это двумя путями. Первый метод включает в себя написание коэффициентов треугольником, как показано ниже. Это известно как Треугольник Паскаля:
Есть много особенностей в треугольнике. Найдите столько, сколько сможете.
Возможно вы нашли путь, как записать следующую строку чисел, используя числа в строке выше. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b) 6 путем добавления следующей строки, используя особенности, которые мы нашли:
Мы видим, что в последней строке
первой и последнее числа 1;
второе число равно 1 + 5, или 6;
третье число это 5 + 10, или 15;
четвертое число это 10 + 10, или 20;
пятое число это 10 + 5, или 15; и
шестое число это 5 + 1, или 6.
Таким образом, выражение (a + b) 6 будет равно
(a + b) 6 = 1a 6 + 6a 5 b + 15a 4 b 2 + 20a 3 b 3 + 15a 2 b 4 + 6ab 5 + 1b 6 .
Для того, чтобы возвести в степень (a + b) 8 , мы дополняем две строки к треугольнику Паскаля:
Тогда
(a + b) 8 = a 8 + 8a 7 b + 28a 6 b 2 + 56a 5 b 3 + 70a 4 b 4 + 56a 3 b 5 + 28a 2 b 6 + 8ab 7 + b 8 .
Мы можем обобщить наши результаты следующим образом.
Бином Ньютона с использованием треугольника Паскаля
Для любого бинома a+ b и любого натурального числа n,
(a + b) n = c0a n b 0 + c1a n-1 b 1 + c2a n-2 b 2 + . + cn-1a 1 b n-1 + cna 0 b n ,
где числа c0, c1, c2. cn-1, cn взяты с (n + 1) ряда треугольника Паскаля.
Пример 1 Возведите в степень: (u — v) 5 .
Решение У нас есть (a + b) n , где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:
1 5 10 10 5 1
Тогда у нас есть
(u — v) 5 = [u + (-v)] 5 = 1(u) 5 + 5(u) 4 (-v) 1 + 10(u) 3 (-v) 2 + 10(u) 2 (-v) 3 + 5(u)(-v) 4 + 1(-v) 5 = u 5 — 5u 4 v + 10u 3 v 2 — 10u 2 v 3 + 5uv 4 — v 5 .
Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.
Пример 2 Возведите в степень: (2t + 3/t) 4 .
Решение У нас есть (a + b) n , где a = 2t, b = 3/t, и n = 4. Мы используем 5-й ряд треугольника Паскаля:
1 4 6 4 1
Тогда мы имеем
Разложение бинома используя значения факториала
Предположим, что мы хотим найти значение (a + b) 11 . Недостаток в использовании треугольника Паскаля в том, что мы должны вычислить все предыдущие строки треугольника, чтобы получить необходимый ряд. Следующий метод позволяет избежать этого. Он также позволяет найти определенную строку — скажем, 8-ю строку — без вычисления всех других строк. Этот метод полезен в вычислениях, статистике и он использует биномиальное обозначение коэффициента 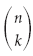
Мы можем сформулировать бином Ньютона следующим образом.
Бином Ньютона с использованием обозначение факториала
Для любого бинома (a + b) и любого натурального числа n,
Бином Ньютона может быть доказан методом математической индукции. Она показывает почему 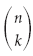
Пример 3 Возведите в степень: (x 2 — 2y) 5 .
Решение У нас есть (a + b) n , где a = x 2 , b = -2y, и n = 5. Тогда, используя бином Ньютона, мы имеем 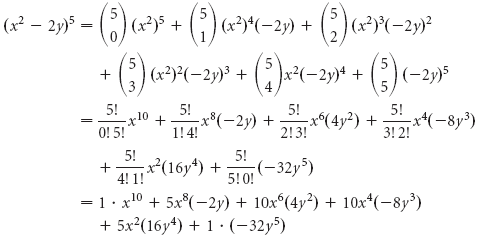
Наконец, (x 2 — 2y) 5 = x 10 — 10x 8 y + 40x 6 y 2 — 80x 4 y 3 + 80x 2 y 4 — 35y 5 .
Пример 4 Возведите в степень: (2/x + 3√ x ) 4 .
Решение У нас есть (a + b) n , где a = 2/x, b = 3√ x , и n = 4. Тогда, используя бином Ньютона, мы получим
Finally (2/x + 3√ x ) 4 = 16/x 4 + 96/x 5/2 + 216/x + 216x 1/2 + 81x 2 .
Нахождение определенного члена
Предположим, что мы хотим определить тот или иной член термин из выражения. Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.
Обратите внимание, что в биноме Ньютона 
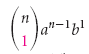

Нахождение (k + 1) члена
(k + 1) член выражения (a + b) n есть 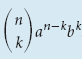
Пример 5 Найдите 5-й член в выражении (2x — 5y) 6 .
Решение Во-первых, отмечаем, что 5 = 4 + 1. Тогда k = 4, a = 2x, b = -5y, и n = 6. Тогда 5-й член выражения будет
Пример 6 Найдите 8-й член в выражении (3x — 2) 10 .
Решение Во-первых, отмечаем, что 8 = 7 + 1. Тогда k = 7, a = 3x, b = -2 и n = 10. Тогда 8-й член выражения будет
Общее число подмножеств
Предположим, что множество имеет n объектов. Число подмножеств, содержащих k элементов есть 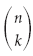

Теперь давайте рассмотрим возведение в степень (1 + 1) n :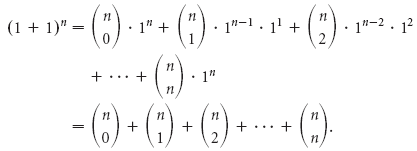
Так. общее количество подмножеств (1 + 1) n , или 2 n . Мы доказали следующее.
Полное число подмножеств
Полное число подмножеств множества с n элементами равно 2 n .
Пример 7 Сколько подмножеств имеет множество ?
Решение Множество имеет 5 элементов, тогда число подмножеств равно 2 5 , или 32.
Пример 8 Сеть ресторанов Венди предлагает следующую начинку для гамбургеров:
<кетчуп, горчица, майонез, помидоры, салат, лук, грибы, оливки, сыр>.
Сколько разных видов гамбургеров может предложить Венди, исключая размеры гамбургеров или их количество?
Решение Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно
. Таким образом, Венди может предложить 512 различных гамбургеров.
Видео:Бином Ньютона. Практическая часть. 10 класс.Скачать

Практическое занятие по теме: «Треугольник Паскаля. Бином Ньютона»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Занятие для студентов 1 курса по теме: « Бином Ньютона. Треугольник Паскаля» (по учебной дисциплине)
Данный конспект занятия по теме: « Бином Ньютона. Треугольник Паскаля» составлено в соответствии с рабочей программой и относится к разделу «Комбинаторика», занятие № 115. Оно предназначено для подготовки студентов первого курса дневного отделения. Материал занятия состоит из методических указаний и упражнений, которые необходимы для усвоения и закрепления изученного материала.
В результате изучения студент должен:
иметь представление о:
биноминальной формуле Ньютона;
принципе построения треугольника Паскаля;
основные приемы разложения на биноминальные коэффициенты;
применять формулу бинома для решения практических заданий;
возводить в любую степень двучлен.
Занятие изучения и первичного закрепления новых знаний
Цель занятия – изучение и первичное осознание нового учебного материала, осмысление связей и отношений в объектах изучения. Познакомить с биномом Ньютона, показать его связь с треугольником Паскаля.
Оборудование занятия: презентация, учебник, приложение.
C одержание занятия
1. Организационный момент
Проверка готовности группы к занятию
2 Т ема, цель и задачи занятия
— обучающая – организовать самостоятельную деятельность учащихся по усвоению понятий – комплексные числа;
создать проблемную ситуацию для следующего урока
— развивающая — формировать умение применять приемы сравнения, обобщения, и навыки воображения учащихся при работе с понятием комплексного числа;
— воспитывающая – формировать умения аккуратного и точного (в соответствии с условиями задания) изображения
Тема занятия “Бином Ньютона. Треугольник Паскаля”.(тему студенты попробуют определить самостоятельно, выполняя задания:
Сегодня на занятии мы должны обобщить и повторить пройденный материал. Полученные знания и навыки в применении биноминальных формул, закрепим на решении математических задач. В течение урока работать будем по группам, затем подведём итог урока, и вы получите домашнее задание.
На экране слайд Актуализация знаний: проверка домашнего задания,
Проверка домашнего задания (наличие)
Пример 1. Найти третий член разложения
Пример 2 Разложить по формуле бином куб разности
Пример 3. Замените * одночленом, чтобы получилось верное равенство:

— Какими формулами вы пользовались в данном задании?
Давайте назовём их и сформулируем.
1. Формулы квадрата суммы и разности двух выражений
2. Формула разности квадратов
3. Формулы суммы и разности кубов
Объяснение нового материала
Формулы сокращённого умножения являются частным случаем бинома Ньютона. Сегодня на занятии обобщим полученные знания и познакомимся с формулами:
Формула бинома Ньютона. Как возвести в степень n сумму двух слагаемых?
Рассмотрим некоторые сведения:
Исаак Ньютон был поистине Великим физиком своего времени, а может быть и величайшим физиком всех времен и народов. Но мы не будем судить об этом. Однако следует заметить, что Ньютон был еще и прекрасным математиком. Кстати формула бинома Ньютона была выгравирована на надгробии его могилы, как самое великое открытие современности того времени!
Кроме формулы бинома Ньютона, со школьной скамьи всем известна формула Ньютона-Лейбница. Таким образом, великий Ньютон вместе с Лейбницем заложили основы дифференциального и интегрального исчисления. Основы теории пределов и строгий подход в математическом анализе был начат и развивался в трудах таких гениев как Огюстен Коши, Георг Кантор, Карл Вейерштрасс. Нельзя, конечно, обойти стороной имя Леонарда Эйлера.
Но мы отвлеклись здесь от основной линии рассуждений. Ведь Формула бинома Ньютона относится к алгебре , а также к ветви математики, называемой комбинаторикой!
Вы спросите: а почему, собственно, формула бинома, и что такое бином вообще. Здесь употребляется алгебраическая терминология: в алгебре есть понятие многочлена. Многочлен это Поли ном — другими словами — сумма произвольного числа слагаемых называется полином.
Например 
А сумма двух слагаемых называется Бином! То есть 
Ньютон изобрел формулу, которая позволяет возвести сумму двух слагаемых в степень с любым показателем, а не только с показателем равным 2! Невозможно переоценить значение формулы бинома Ньютона при решении многих заданий. Поэтому правильно формула, о которой идет здесь речь, называется Формулой Ньютона для степени бинома. Мы не будем сразу писать эту формулу в общем виде, а вначале обратимся к школьной алгебре!
Вспомним из школьного курса что:
Это и есть формула квадрата суммы или формула квадрата двучлена, или формула второй степени бинома! Возведем в третью степень сумму двух слагаемых или вычислим бином третьей степени.
Скобки раскрываем аналогично, используя распределительный или дистрибутивный закон алгебры: 
Пойдем дальше, возведем бином в четвертую степень! Но возводить мы будем, воспользовавшись предыдущей формулой для третьей степени бинома:
Более подробное раскрытие скобок студенты выполняют самостоятельно, проверяем результат раскрытия, так как вычисления аналогичны тому, как это уже проделали при получении формул (а + b) 2 u ( a + b ) 3 .
Итак, мы получили формулу для четвертой степени бинома! Попытаемся возвести в пятую степень бином! Для возведения бинома в пятую степень надо умножить результат возведения бинома в четвертую степень на известный нам бином! Вот в чем заключалась гениальная идея Ньютона!
=
(вместо четвертой степени бинома мы подставляем вычисленное ранее выражение ( a + b ) 4 и снова раскрываем скобки, опуская подробные вычисления, поскольку они выполнялись при вычислении третьей и второй степени бинома.) А сколько же можно так продолжать увеличивать порядок степени возведения бинома? Ответ: до бесконечности можно! Точно также, например при n=101 умножим результат возведения в степень 100 на (а + b) , тогда получим результат возведения в степень 100.
Но мы не будем расписывать все это выражение, поскольку после приведения подобных членов оно имеет 101 слагаемое и не уместится в одну строчку, а в десять строчек прочтение будет очень затруднительно!
Но гениальность Ньютона в том и заключалось, что он смог записать эту формулу в общем виде в одну строчку для любого n , то есть формулу вида:
Здесь можно сделать вывод: чтобы получить формулу для степени n, надо знать эту формулу для (n-1). Чтобы знать формулу для (n-1) надо получить ее (n-1) раз так, как мы это делали для 2,3,4, и 5-й степени, то есть умножали уже известный результат для степени на единицу меньшей заданной степени на степень равную единице!
А теперь второй вывод: все эти действия, которые приводят к формуле бинома для степени ( n-1) можно записать более кратко?! Тогда можно будет не переписывать (n-1) раз фактически одни и те же вычисления для 2, 3, 4, 5, 6. n-1 степени бинома, а записать их одной формулой, умножить эту формулу еще раз на первую степень бинома и полностью доказать искомую формулу! Вот вам и алгоритм рассуждений Ньютона!
Здесь мы выделили последние предложения жирным шрифтом, поскольку они являются основой доказательства формулы бинома Ньютона и наиболее серьезным и сложным шагом во всех наших рассуждениях — метод математической индукции один из наиболее важных методов математики. Но как же записать общую формулу для степени бинома, равной n-1? Для ответа используем уже доказанные формулы степени бинома, равные 2, 3,4,и 5.
Обратим внимание, что коэффициенты крайних слагаемых равны 1, показатели степени — наивысшие (n). Показатели степени переменных изменяются в обратной зависимости, а вот определить коэффициенты достаточно сложно. Имеет смысл вернуться к определению сочетания из n элементов по m, где
n – степень бинома, а m является номером слагаемого, начиная с 0. Тогда для 3 степени бинома мы получим следующие коэффициенты:
Можно, конечно, привести вывод формулы бинома, что не входит в нашу программу, поэтому запишем эту формулу без доказательства и используем ее для получения общей формулы:
где — сигма, знак суммы слагаемых от 0 до n.
Итак, Если мы имеем бином (а — b ) ⁿ , то знаки слагаемых чередуются.
Однако, вычислять коэффициенты через сочетания достаточно сложно. Чтобы облегчить эти вычисления, используют: Треугольник Паскаля:
Каждому студенту даем Раздаточный материал
Видео:БИНОМ Ньютона | треугольник ПаскаляСкачать

Бином Ньютона
 Формула бинома Ньютона Формула бинома Ньютона |
 Связь бинома Ньютона с треугольником Паскаля Связь бинома Ньютона с треугольником Паскаля |
 Свойства биномиальных коэффициентов Свойства биномиальных коэффициентов |
Видео:Треугольник ПаскаляСкачать

Формула бинома Ньютона
В Таблице 1 из раздела «Формулы сокращенного умножения» приведены формулы для натуральных степеней бинома
в случаях, когда n = 1, 2, 3, 4, 5, 6.
В настоящем разделе рассматривается общий случай этой формулы, т.е. случай произвольного натурального значения n .
Утверждение . Для любого натурального числа n и любых чисел x и y справедлива формула бинома Ньютона :
– числа сочетаний из n элементов по k элементов.
В формуле (1) слагаемые
называют членами разложения бинома Ньютона , а числа сочетаний 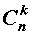
Если в формуле (1) заменить y на – y , то мы получим формулу для n — ой степени разности:
Видео:Бином Ньютона и треугольник Паскаля | Учитель года Москвы — 2020Скачать

Связь бинома Ньютона с треугольником Паскаля
Напомним, что треугольник Паскаля имеет следующий вид:
| № | Треугольник Паскаля |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| … | … |
Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:
| № | Треугольник Паскаля |
| 0 | 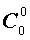 |
| 1 | 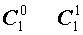 |
| 2 | 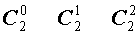 |
| 3 | 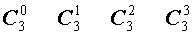 |
| 4 | 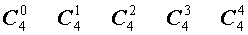 |
| 5 | 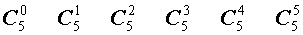 |
| 6 | 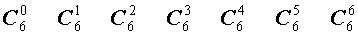 |
| … | … |
| Треугольник Паскаля |
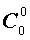 |
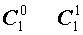 |
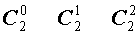 |
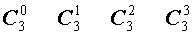 |
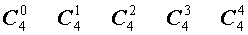 |
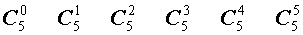 |
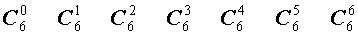 |
| … |
| Треугольник Паскаля |
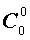 |
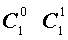 |
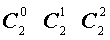 |
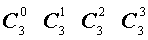 |
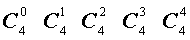 |
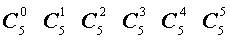 |
| … |
Видео:✓ Бином Ньютона. Игра в слова. Числа сочетаний | Комбинаторика | Ботай со мной #057 | Борис ТрушинСкачать

Свойства биномиальных коэффициентов
Для биномиальных коэффициентов справедливы равенства:
| 1 | 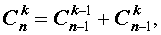 |
| 2 |