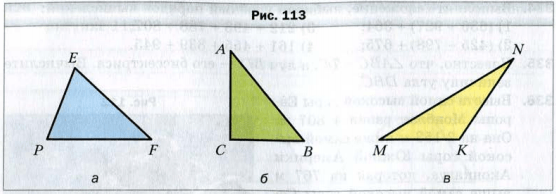
Из всех многоугольников треугольники имеют наименьшее количество углов и сторон.
Треугольники можно различать по виду их углов.
Есди все углы треугольника острые, то его называют остроугольным треугольником (рис. 113, а).
Если один из углов треугольника прямой, то его называют прямоугольным треугольником (рис. 113, б).
Если один из углов треугольника тупой, то его называют тупоугольным треугольником (рис. 113, в).
Говорят, что мы классифицировали треугольники по виду их углов.
Треугольники можно классифицировать не только по виду углов, но и по количеству равных сторон.
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
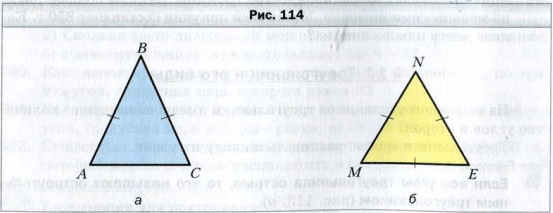
На рисунке 114, а изображен равнобедренный треугольник ABC, у которого AB = BC. На рисунке равные стороны отмечают равным количеством черточек. Равные стороны AB и BC называют боковыми сторонами, а сторону AC − основанием равнобедренного треугольника ABC.
Если стороны треугольника равны, то его называют равносторонним треугольником.
Треугольник, изображенный на рисунке 114, б, − равносторонний, у него MN = NE = EM.
Треугольник, у которого три стороны имеют различную длину, называют разносторонним треугольником.
Треугольники, изображенные на рисунке 113, − разносторонние. Если сторона равностороннего треугольника равна a, то его периметр вычисляют по формуле:
P = 3 a
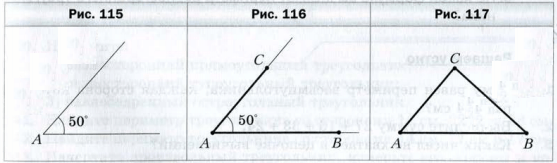
Пример 1 . С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3 см и 2 см, а угол между ними − 50 °.
С помощью транспортира построим угол A, градусная мера которого 50 ° (рис. 115 ). На сторонах этого угла от его вершины с помощью линейки отложим отрезок AB длиной 3 см и отрезок AC длиной 2 см (рис. 116 ). Соединив отрезком точки B и C, получим искомый треугольник ABC ( рис. 117 ).
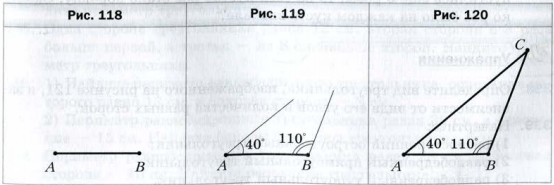
Пример 2 . С помощью линейки и транспортира постройте треугольник ABC, сторона AB которого равна 2 см, а углы CAB и CBA соответственно равны 40 ° и 110 °.
Решение. С помощью линейки строим отрезок AB длиной 2 см (рис. 118 ). От луча AB с помощью транспортира откладываем угол с вершиной в точке A, градусная мера которого равна 40 °. От луча BA в ту же сторону от прямой AB, в которую был отложен первый угол, откладываем угол с вершиной в точке B, градусная мера которого равна 110 °(рис. 119 ).
Найдя точку C пересечения сторон углов A и B, получаем искомый треугольник ABC ( рис. 120 ).
- Геометрия. Урок 3. Треугольники
- Определение треугольника
- Виды треугольников
- Отрезки в треугольнике
- Площадь треугольника
- Равнобедренный треугольник
- Равносторонний треугольник
- Прямоугольный треугольник
- Теорема Пифагора
- Примеры решений заданий из ОГЭ
- Треугольник. Формулы определения и свойства треугольников.
- Определение треугольника
- Классификация треугольников
- 1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
- 2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
- 3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
- 4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
- 5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
- 6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
- Свойства треугольника
- 1.Свойства углов и сторон треугольника.
- 2.Теорема синусов.
- 3. Теорема косинусов.
- 4. Теорема о проекциях
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- 🎬 Видео
Видео:Виды треугольниковСкачать

Геометрия. Урок 3. Треугольники
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение треугольника
- Виды треугольников
- Отрезки в треугольнике
Видео:Виды треугольниковСкачать

Определение треугольника
Треугольник – многоугольник с тремя сторонами и тремя углами.
Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .
Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .
Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Виды треугольников
Треугольник остроугольный , если все три угла в треугольнике острые.
Треугольник прямоугольный , если у него один из углов прямой ( = 90 ° ) .
Треугольник тупоугольный , если у него один из углов тупой.

Основные свойства треугольника:
- Против большей стороны лежит больший угол.
- Против равных сторон лежат равные углы.
- Сумма углов в треугольнике равна 180 ° .
- Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .
Видео:Виды треугольников 3 классСкачать

Отрезки в треугольнике
Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.
Свойства биссектрис треугольника:
- Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
- Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:
Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Свойства медиан треугольника:
- Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.
Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.
Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Площадь треугольника
Площадь произвольного треугольника можно найти следующими способами:
- Полупроизведение стороны на высоту, проведенную к этой стороне.
Видео:Геометрия 7 кл. Треугольники. Определение. Обозначение. Компоненты. Особенности. Виды треугольников.Скачать

Равнобедренный треугольник
Равнобедренным называется треугольник, у которого две стороны равны.
Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.
Видео:ТреугольникСкачать

Равносторонний треугольник
Равносторонним называется треугольник, у которого все стороны и все углы равны.
Площадь равностороннего треугольника находится по формуле S = a 2 3 4
Высота равностороннего треугольника находится по формуле h = a 3 2
Видео:Треугольники. 7 класс.Скачать

Прямоугольный треугольник
Треугольник называется прямоугольным, если у него один из углов равен 90 ° .
Свойства прямоугольного треугольника:
- Сумма двух острых углов треугольника равна 90 ° .
- Катет, лежащий напротив угла в 30 ° , равен половине гипотенузы.
- Если катет равен половине гипотенузы, он лежит напротив угла в 30 ° .
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Теорема Пифагора
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с треугольниками
Видео:Треугольники: остро-, тупо- и прямоугольныеСкачать

Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Видео:виды и названия треугольников по сторонамСкачать

Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Видео:9 класс, 15 урок, Решение треугольниковСкачать

Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Видео:Математика 5 класс (Урок№28 - Треугольники.)Скачать

Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
🎬 Видео
ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Найдите третью сторону треугольникаСкачать

Признаки равенства треугольников. 7 класс.Скачать

Математика 6 класс. Треугольник. Виды треугольников. ЕГЭ, ОГЭ, ЦТ, экзаменСкачать

Треугольник и его виды. 5 классСкачать