О чем эта статья:
- Первый признак равенства треугольников
- Второй признак равенства треугольников
- Третий признак равенства треугольников
- Треугольник. Формулы и свойства треугольников.
- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Треугольник
- Треугольник произвольный
- Свойства
- Признаки равенства треугольников
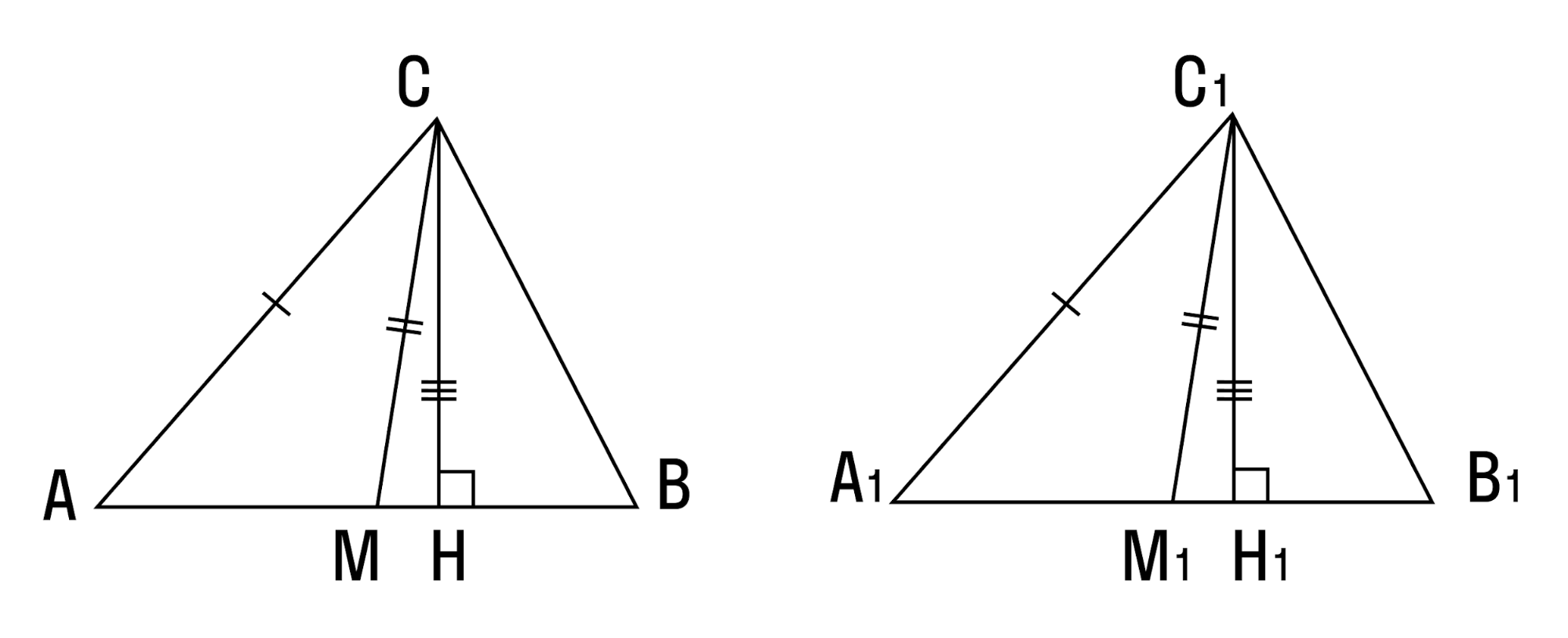
- Биссектриса, высота, медиана
- Средняя линия треугольника
- Вписанная окружность
- Описанная окружность
- Соотношение сторон в произвольном треугольнике
- Площадь треугольника
- 🌟 Видео
Видео:Вычислить определитель 3 порядка. Правило треугольникаСкачать

Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
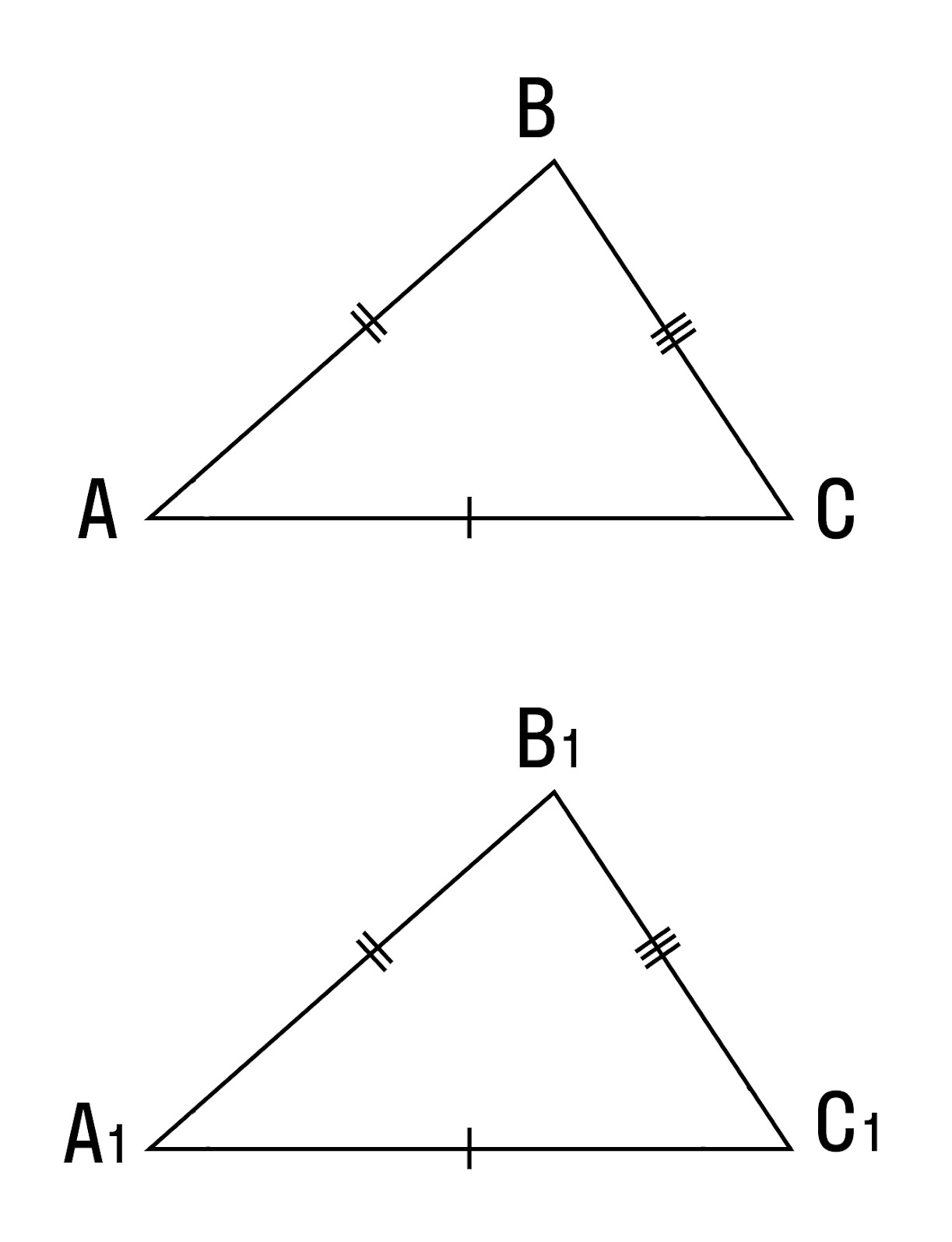
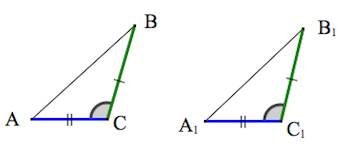
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Второй признак равенства треугольников
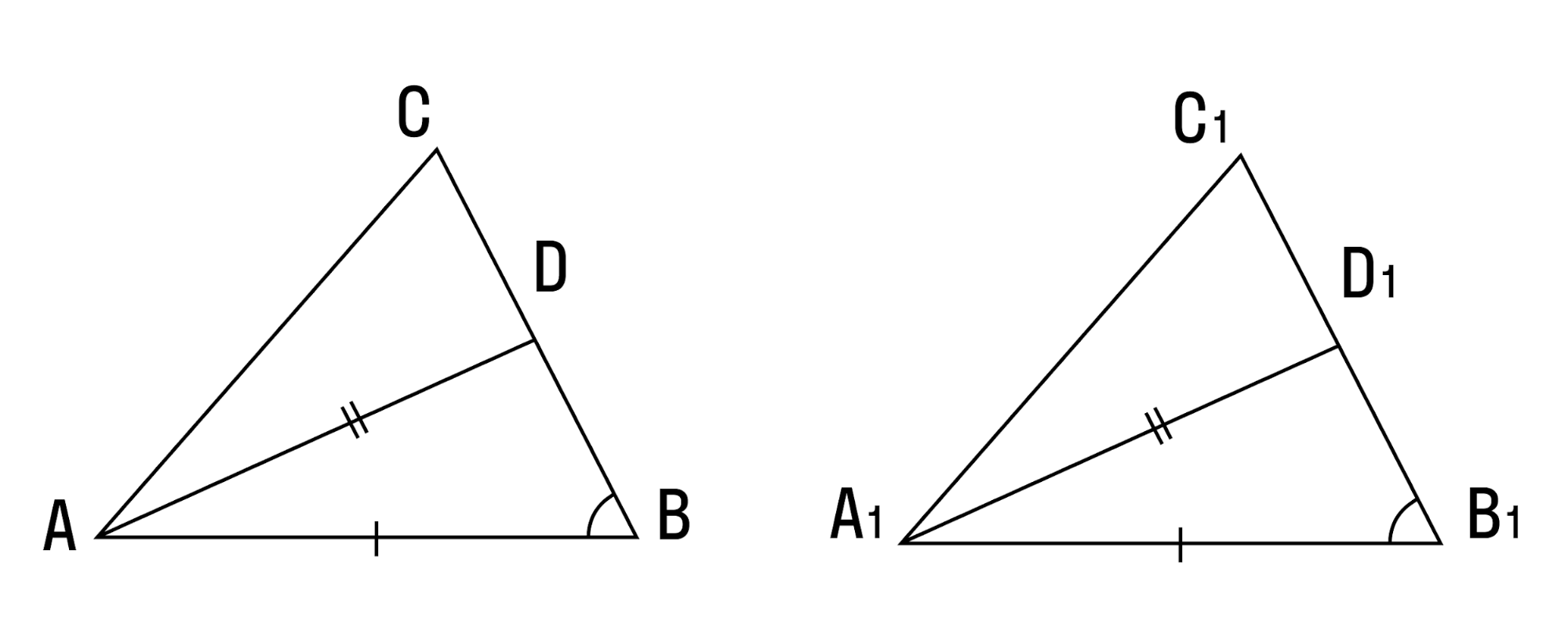
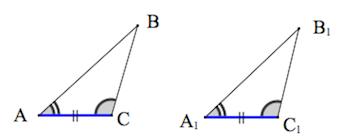
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Видео:Признаки равенства треугольников. 7 класс.Скачать

Третий признак равенства треугольников
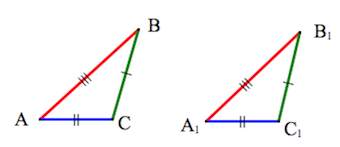
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
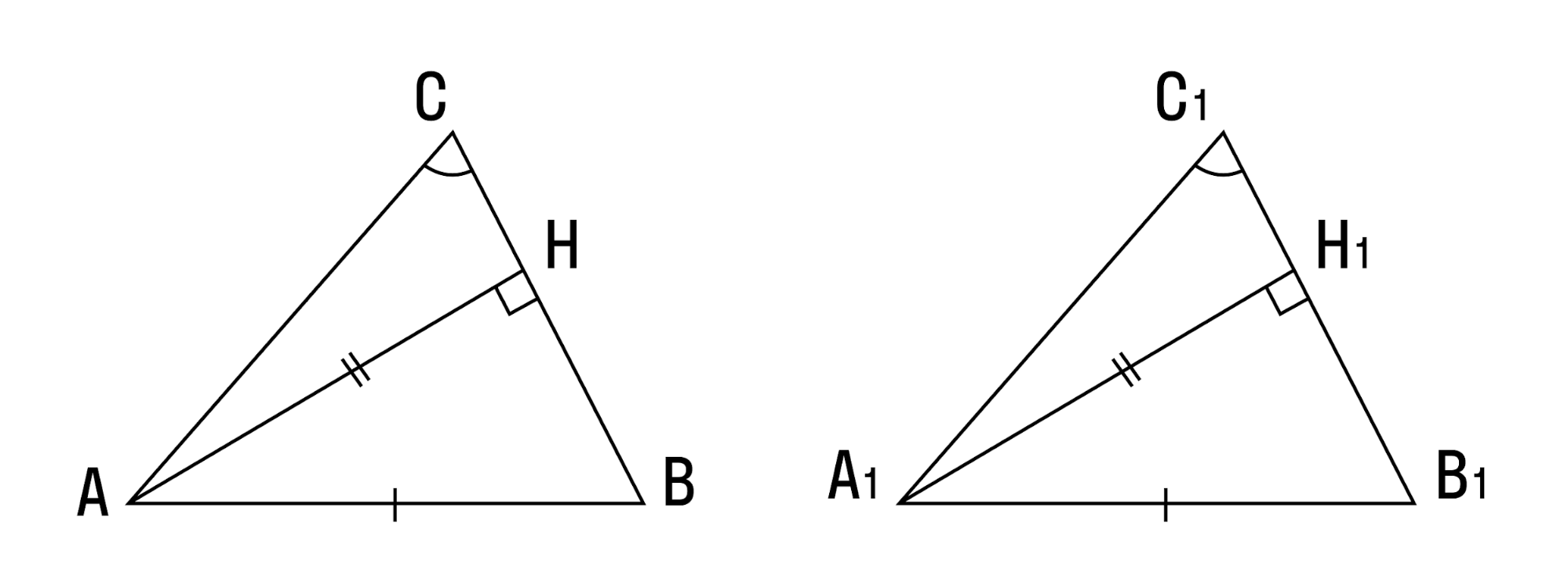
- Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
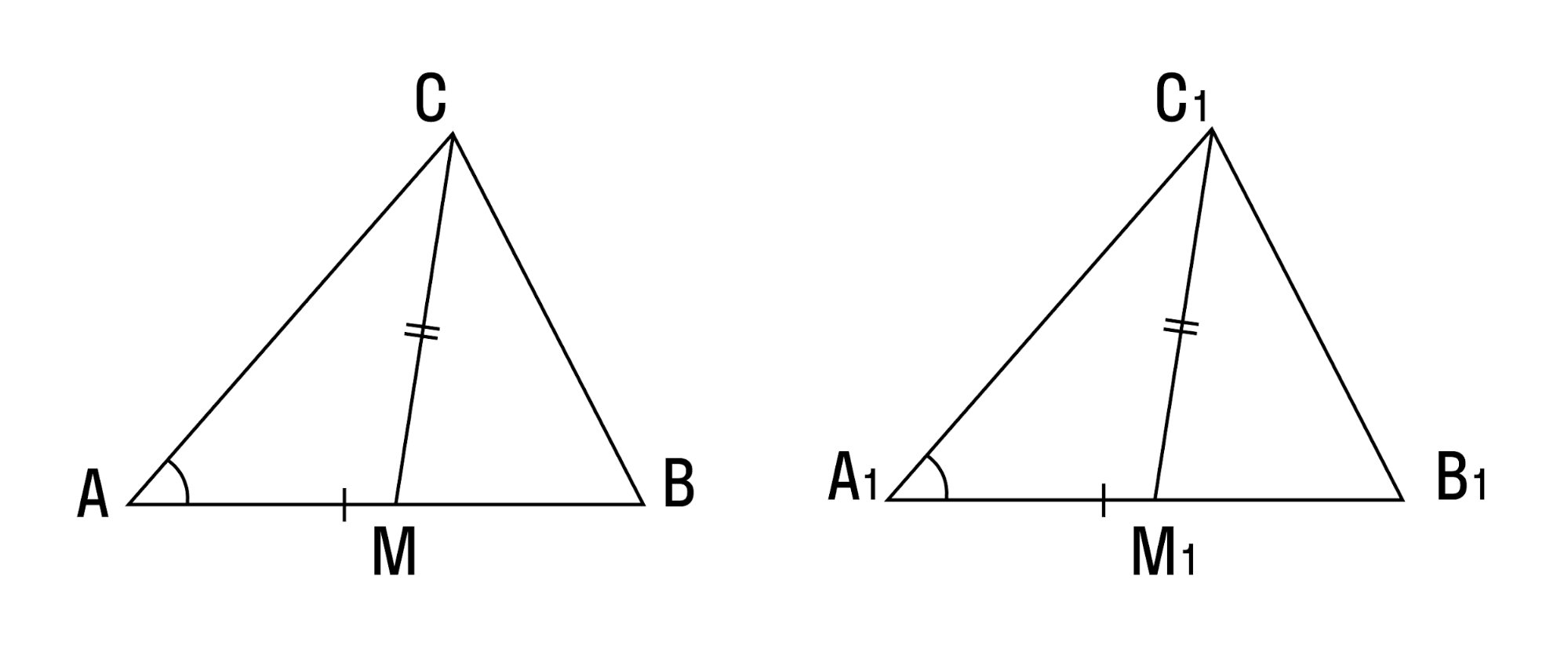
- Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
- Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
- Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
- Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
Видео:Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Треугольник. Формулы и свойства треугольников.
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Определитель матрицы 3 порядка. Как легко найти? Метод треугольников и Саррюса. Просто и наглядноСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Первый признак равенства треугольников. 7 класс.Скачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Треугольники. 7 класс.Скачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:Математика 3 класс. Виды треугольниковСкачать

Связь между вписанной и описанной окружностями треугольника
Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:Бестселлер Все правила по геометрии за 7 классСкачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Треугольник
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
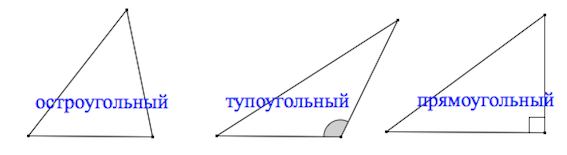
Виды треугольников :+ показать
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
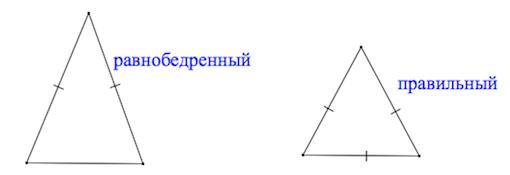
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º .
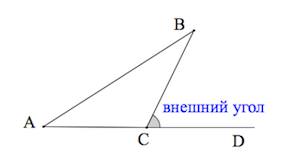
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
Признаки равенства треугольников
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
Средняя линия треугольника
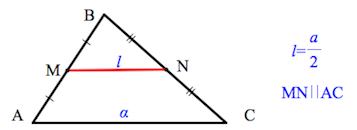
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
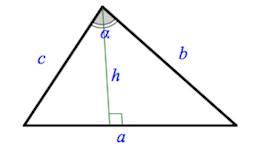
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
, где
– полупериметр
Смотрите также площадь треугольника здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!
В разделе свойства:
Да, не хватало значка «» у А. Спасибо! 😉
Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
спасибо я так и думал а то не могу решить и всё
СПАСИБО!
Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Очевидно,
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти
Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно
🌟 Видео
Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать