Вписать три окружности в одну окружность (5 видео)

Задача про круги: кажется сложной, но она очень простая!

Раздумывая над решением, не спешите сдаваться. Все гораздо легче, чем вам может показаться на первый взгляд. И пусть здесь нет программирования, зато есть возможность развивать логическое мышление.

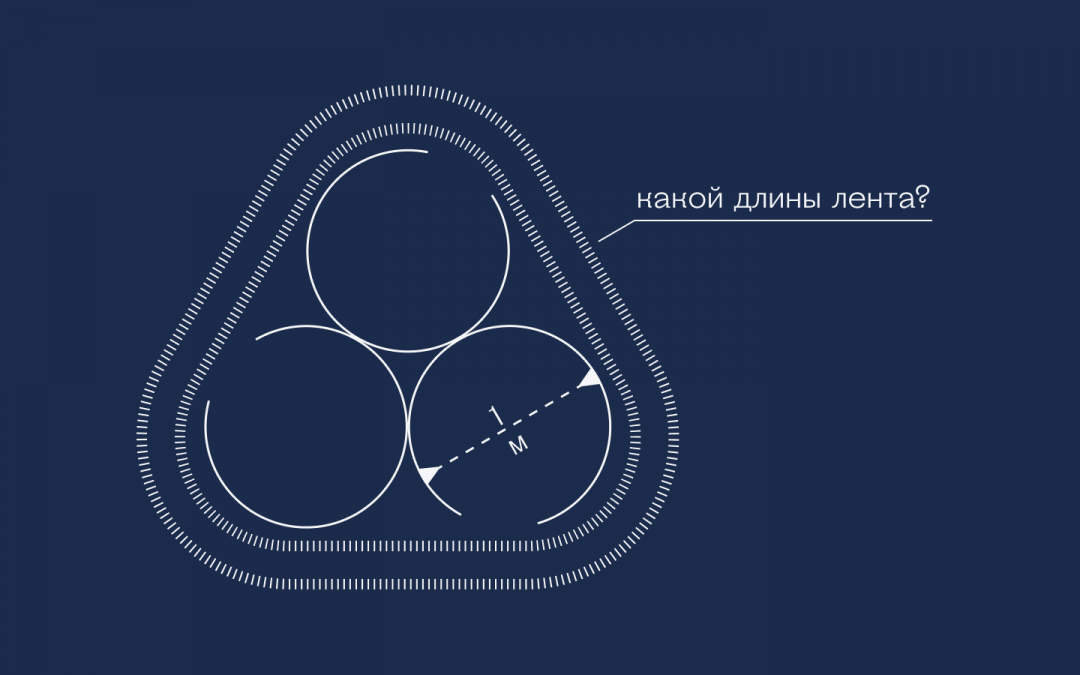
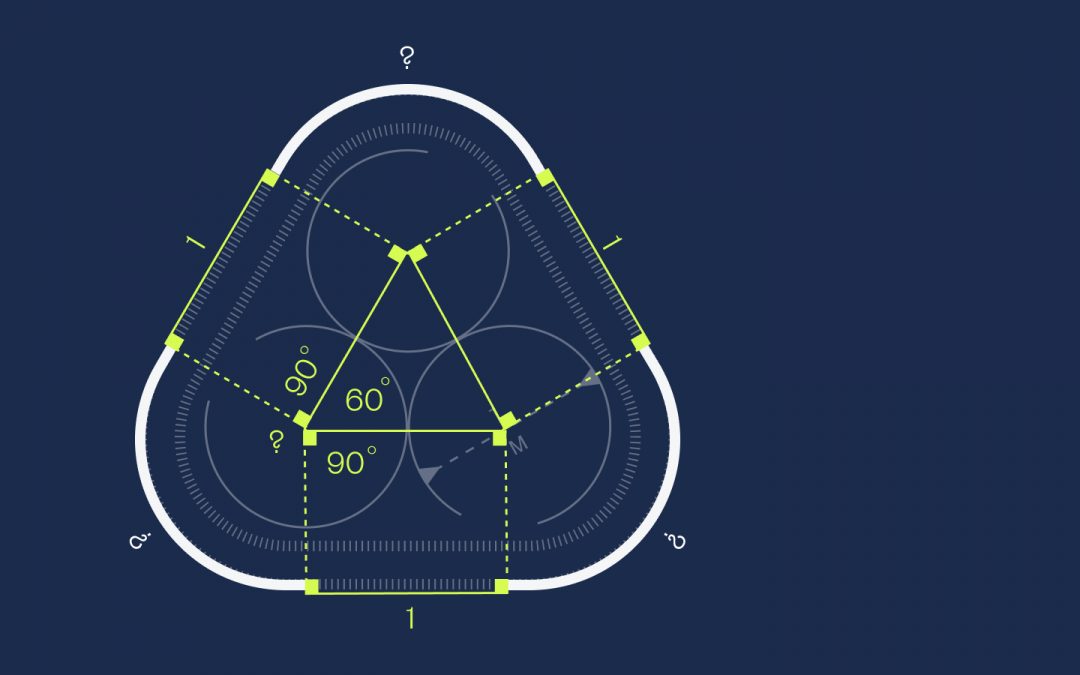
Условие: даны три одинаковых соприкасающихся круга диаметром 1 м. Их опоясывает эластичная лента.

Задание: найдите длину ленты, натянутой вокруг кругов.

Для того чтобы найти ответ, вам не нужны сложные формулы, такие как расчет кривизны и т.п. На самом деле все гораздо проще.

Содержание

Строим треугольник
Создаем проекцию
Находим длину секций
Сколько малых одинаковых окружностей радиуса r можно вписать в большую окружность радиуса R
Простая задача про круги, которая выглядит сложной
Строим внутренний треугольник
Строим проекцию
Вычисляем длину секций
🎦 Видео

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Строим треугольник

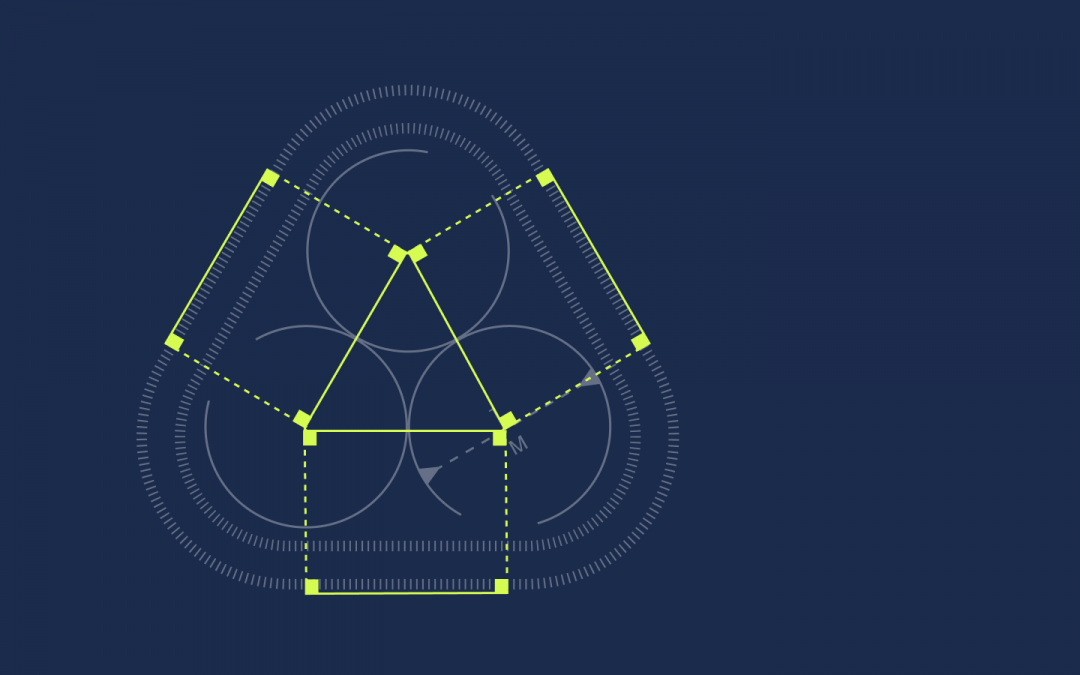
Для начала соединим центры кругов таким образом, чтобы получился треугольник.

По законам геометрии, центры соприкасающихся кругов можно соединить прямой линией, причем точка касания будет находиться именно на ней. Так как диаметр равен 1 метру, радиусы всех кругов равны 0,5 метра. Укажем это на схеме:

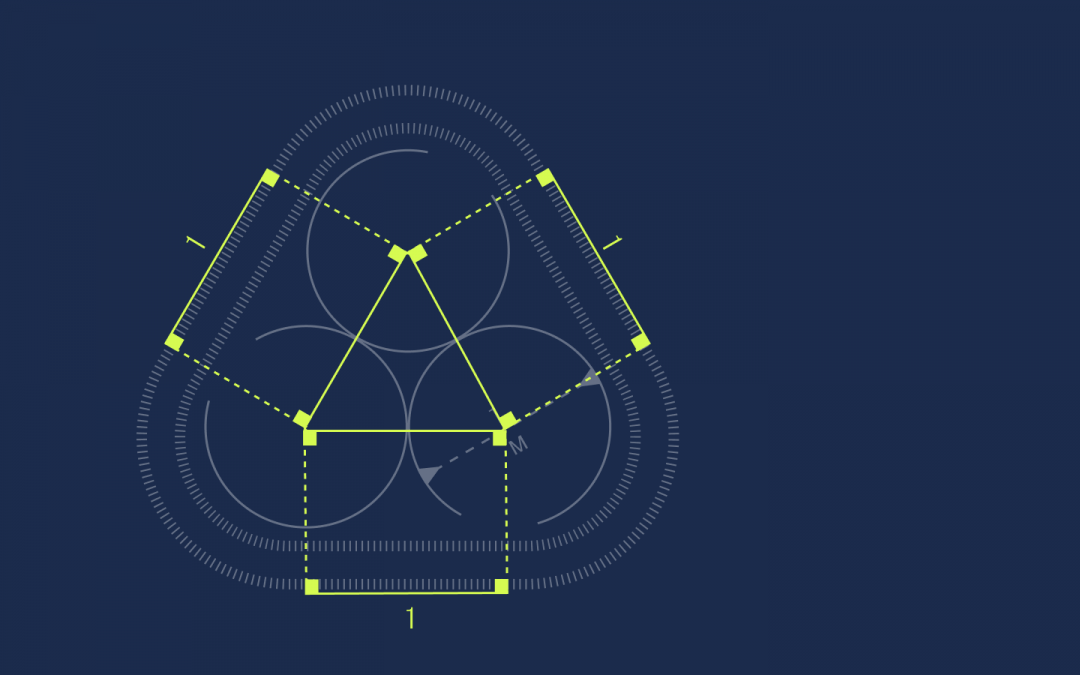
Выходит, что стороны треугольника равны между собой и длина каждой из них составляет 0,5 + 0,5 = 1. Зафиксируем это и двигаемся дальше.

Видео:Три окружностиСкачать

Создаем проекцию

Все вершины треугольника соединим с лентой линиями, проведенными под углом 90°.

Получились прямоугольники. Как известно, противоположные стороны этой фигуры равны, а раз длина каждой стороны треугольника равна 1, данные отрезки ленты также равны 1:

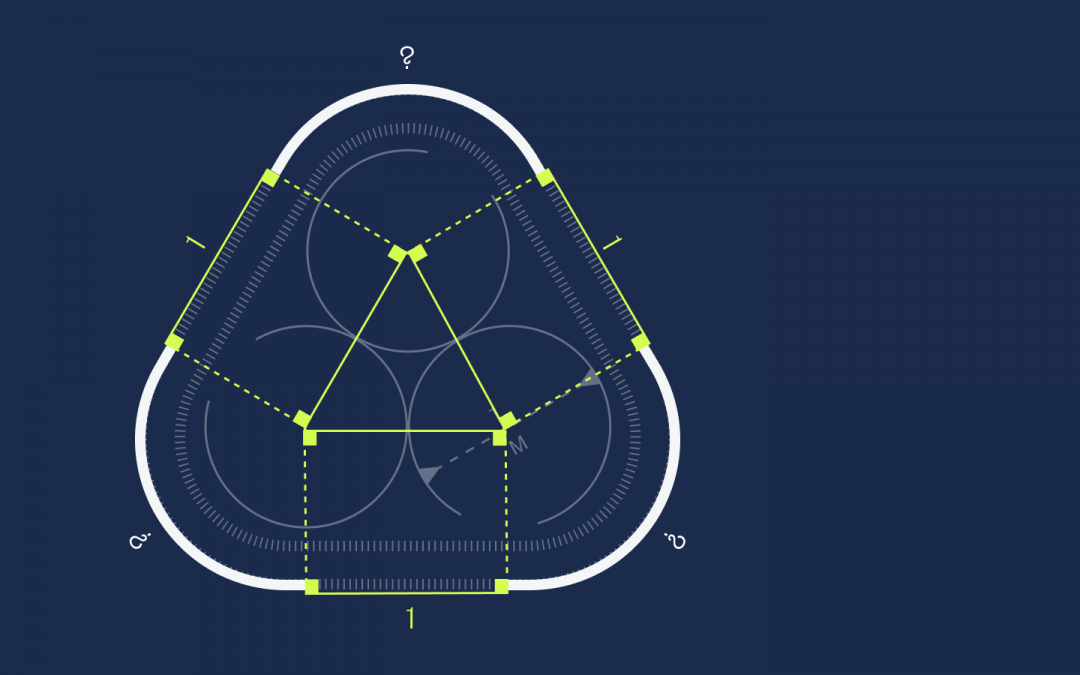
Теперь нужно найти длину трех оставшихся секций:

Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Находим длину секций

В круге 360 градусов. Треугольник, который мы построили из центров кругов, равносторонний. Следовательно, каждый угол в нем равен 60°. У прямоугольников углы по 90°. Обозначим все это на схеме:

Находим неизвестный угол:

90 + 60 + 90 + X = 360

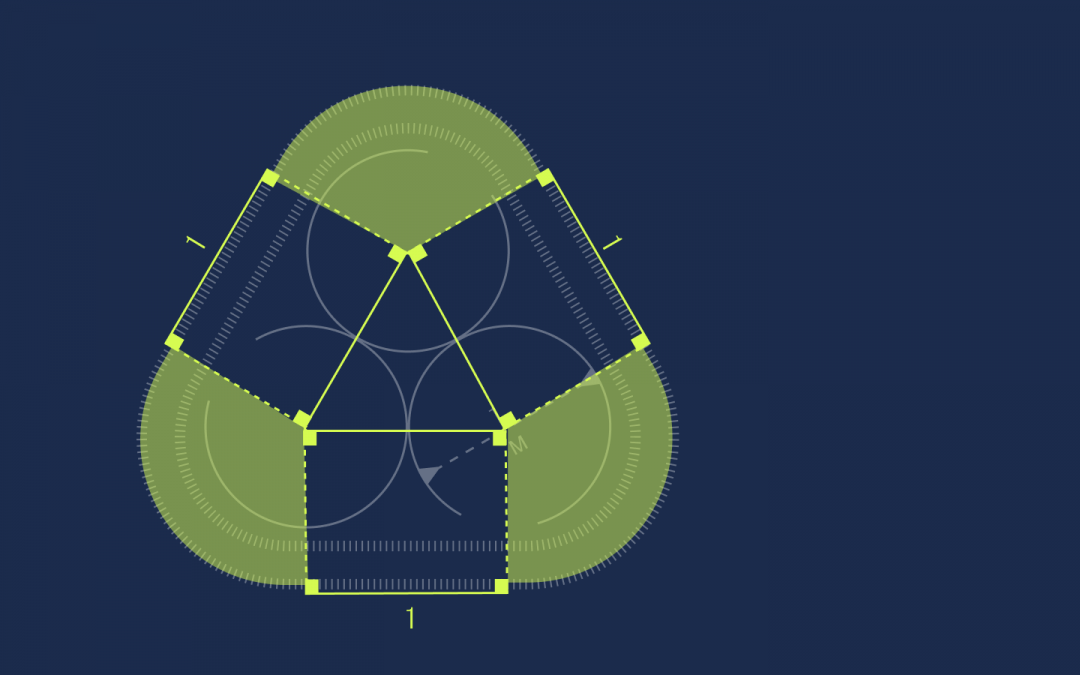
120° — это ровно одна третья часть круга, а мы имеем 3 таких части:

Получается, что все вместе они формируют один полный круг. Нам известно, что радиус данного круга равен 0,5, а диаметр – 1. Это позволяет вычислить длину окружности:

Прибавляем к этому числу длины 3-х отрезков и получаем длину всей ленты: 3 + π.

Видео:Деление окружности на 3 частиСкачать

Сколько малых одинаковых окружностей радиуса r можно вписать в большую окружность радиуса R

Этот калькулятор оценивает число малых окружностей заданного радиуса r можно разместить внутри большой окружности заданного радиуса R.

Этот калькулятор выводит максимальное число малых окружностей заданного радиуса r можно разместить внутри большой окружности заданного радиуса R. Например это могут быть малые трубы внутри большой, провода в кабель канале, круги, вырезаемые из круговой же заготовки и так далее.

Вы можете подумать, что для решения такой задачи должна быть выведена формула, но на самом деле это не так — формулы нет. Эта задача относится к классу оптимизационных задач, а точнее, задач упаковки. Эта задача известна как Упаковка кругов в круге. Упаковка кругов в круге — это двумерная задача упаковки, целью которой является упаковка единичных кругов в как можно меньший круг. См. Упаковка кругов в круге.

Для этой задачи найденное решение еще и должно быть проанализировано на оптимальность. Статья в википедии по ссылке выше приводит первые 20 решений (иными словами, приводит минимальные радиусы больших окружностей вмещающих заданное число единичных окружностей. Между прочим, по умолчанию входные параметры калькулятора дают ответ 11 кругов, что соответствует следующей диаграмме:

Хорошей новостью является то, что есть проект в интернете, целиком посвященный задачам упаковки — сайт Packomania. На сегодняшний день он содержит все найденные решения, автор сайта, Экард Спехт (Eckard Specht), сам участвует в поиске решений, и большинство решений, на самом деле найдены им. Оттуда можно взять соотношения r к R для решений, позволяющих упаковать от 1 до 2600 окружностей внутри большой, с графическими диаграммами решения.

Соотношения r/R, приведенные на сайте и использует калькулятор ниже для поиска оптимального решения. Если соотношение не попадает в диапазон известных решений, калькулятор выдает ошибку.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Простая задача про круги, которая выглядит сложной

Но на деле она точно простая.

Разберём свежую задачу с канала MindYourDecisions. Это не про программирование, но развивает логическое мышление.

Дано: есть три одинаковых круга с диаметром в 1 метр. Круги соприкасаются друг с другом, а вокруг них натянута эластичная лента.

Что нужно: найти длину этой ленты.

Кажется, что это очень сложная задача, где нужно знать сложные формулы расчёта кривизны и точек натяжения, но на деле всё будет гораздо проще. Если знаете английский — посмотрите оригинальный ролик, там классная анимация:

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Строим внутренний треугольник

Первое, что мы сделаем, — соединим центры всех кругов в один треугольник:

В геометрии есть такое правило, что если круги касаются друг друга, то через их центры можно провести прямую линию, и точка касания кругов будет лежать на этой линии. Раз у нас диаметр равен 1, то радиус каждого круга равен 0,5. Обозначим это на рисунке:

Получается, что длина каждой стороны треугольника равна 0,5 + 0,5 = 1. Запомним это и идём дальше.

Видео:Если в четырёхугольник можно вписать окружностьСкачать

Строим проекцию

От каждой вершины треугольника проведём под прямым углом линии к ленте:

Получились прямоугольники. У прямоугольников противоположные стороны равны, поэтому раз стороны треугольника равны единице, то и эти отрезки на ленте тоже будут равны единице:

Осталось найти длину оставшихся секций:

Видео:Деление окружности на равные части с помощью циркуляСкачать

Вычисляем длину секций

Здесь нам поможет знание о том, что полный оборот внутри круга — это 360 градусов.

Так как во внутреннем треугольнике все стороны равны, то это равносторонний треугольник. А раз так, то углы в нём равны 60 градусов. Добавим сюда по два прямых угла по 90 градусов из прямоугольников:

Решаем уравнение: 90 + 60 + 90 + X = 360 → X = 120 градусов.

Но 120 градусов — это ровно треть круга, а у нас таких частей как раз три:

Это значит, что из них можно составить один целый круг. При этом мы знаем, что у этого круга радиус 0,5, а диаметр тогда равен единице. Этого достаточно, чтобы посчитать длину окружности: L = π × d → L = 3,14.

Складываем это число с длинами трёх отрезков и получаем полную длину: 3 + π