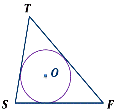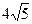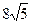Вписанные описанные треугольники тест

Тест по теме «Вписанная и описанная окружности треугольника» по геометрии 7 класс к учебнику Мерзляк А. Г.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Скачать:

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Предварительный просмотр:

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №23»

МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОДСКОЙ ОКРУГ

СИМФЕРОПОЛЬ РЕСПУБЛИКИ КРЫМ

«Описанная и вписанная окружности треугольника»

Работу выполнил: Рычкова Ирина Владимировна

учитель высшей категории

При решении задач используют инструменты:

• циркуль, транспортир, линейку
• линейку, угольник
• циркуль, транспортир, линейку, угольник
• циркуль, линейку

Центром вписанной окружности является точка пересечений.

• его медиан
• его биссектрис
• его высот
• его серединных перпендикуляров

В любой треугольник можно вписать окружность?

Где всегда находится центр вписанной окружности в треугольник?

• внутри окружности
• на окружности
• вне окружности

Какую окружность называют описанной около треугольника?

• если она проходит через все вершины треугольника
• если она касается всех сторон треугольника
• если она описывает треугольник

Около любого треугольника можно описать окружность?

Центром описанной окружности около треугольника является точка пересечения.

• его биссектрис
• его медиан
• его высот
• его серединных перпендикуляров

Прямую, имеющую с окружностью только одну общую точку, называют.

• касательной к окружности
• секущей окружности
• пересекающей окружность

Касательная к окружности . радиусу, проведённому в точку касания.

• перпендикулярна
• параллельна
• симметрична

Какую окружность называют вписанной в треугольник?

• если она касается всех его сторон
• если она проходит через его вершины
• если она лежит внутри треугольника

Окружность, вписанная в треугольник АВС, касается сторон треугольника соответственно в точках М, К и Е, ВК = 2 см, КС = 4 см, АМ = 8 см. Найдите периметр треугольника АВС.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Разработка урока по геометрии 9 класс «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности»

Разработка урока-изучения нового материала по геометрии в 9 классе «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности» Конспект урока по геомет.

Презентация к уроку по геометрии (8 класс) на тему: » Вписанная окружность»

Презентация к уроку.

«Описанная и вписанная окружности треугольника. Урок решения одной задачи»

Учебник: Л.С. Атанасян, В.Ф. Бутусов «Геометрия, 7 – 9»Тема урока: «Описанная и вписанная окружности треугольника. Урок решения одной задачи»Цели урока: научить учащихся анализировать теоретичес.

Презентация по геометрии 8 класс Вписанная окружность. Описанная окружность.

Данная презентация содержит определения и свойства вписанной окружности и описанной окружности около многоугольника (треугольник). В презентации рассмотрены несложные задачи.

Презентация по геометрии 8 класс «Вписанная окружность Описанная окружность».

Понятие окружности вписанной в треугольник и описанной около треугольника.

Методическая разработка урока английского языка по теме «Описание внешности человека. Его одежда. Цвета» в 5 классе

Данная методическая разработка направлена на формирование умения строить развернутое монологическое высказывание с опорой на прослушанный/прочитанный текст по теме «Описание внешности человека. .

Тест по теме «Правильный многоугольник. Вписанная и описанная окружности. Формулы площади правильного многоугольника , стороны правильного многоугольника и радиуса вписанной окружности в правильный многоугольник»

Тест по теме «Правильный многоугольник. Вписанная и описанная окружности. Формулы площади правильного многоугольника , стороны правильного многоугольника и радиуса вписанной окр.

Видео:Тема 7. Вписанные и описанные окружности треугольникаСкачать

Тест по теме «Треугольник. Вписанные и описанные окружности»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Тест по теме «Треугольник. Вписанная и описанная окружности»

Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 183.

Найдите хорду, на которую опирается угол 30 O , вписанный в окружность радиуса 27.

К окружности, вписанной в треугольник ABC , проведены три касательные. Периметры отсеченных треугольников равны 8, 23, 78. Найдите периметр данного треугольника.

В треугольнике АВС, АС=24, ВС=7 угол С равен 90°. Найдите радиус вписанной окружности .

Катеты равнобедренного прямоугольного треугольника равны 6+3 . Найдите радиус окружности, вписанной в этот треугольник.

В прямоугольный треугольник вписана окружность радиусом 5 м. Периметр треугольника равен 78 м. Найти радиус описанной окружности.

Точка касания боковой стороны равнобедренного треугольника и вписанной в этот треугольник окружности делит боковую сторону в отношении 5:8, считая от вершины основания треугольника.

Во сколько раз боковая сторона этого треугольника больше его основания?

Тест по теме «Треугольник. Вписанная и описанная окружности».

Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника .

Найдите хорду, на которую опирается угол 30 O , вписанный в окружность радиуса 43.

К окружности, вписанной в треугольник ABC , проведены три касательные. Периметры отсеченных треугольников равны 10, 32, 24.

Найдите периметр данного треугольника.

В треугольнике АВС, АС=12, ВС=16 угол С равен 90°. Найдите радиус вписанной окружности .

Катеты равнобедренного прямоугольного треугольника равны 8+4 . Найдите радиус окружности, вписанной в этот треугольник.

В прямоугольный треугольник вписана окружность радиусом 10 м. Периметр треугольника равен 122 м. Найти радиус описанной окружности.

Точка касания боковой стороны равнобедренного треугольника и вписанной в этот треугольник окружности делит боковую сторону в отношении 10:13, считая от вершины основания треугольника. Во сколько раз боковая сторона этого треугольника больше его основания?

Тест по теме «Треугольник. Вписанная и описанная окружности».

Найдите радиус окружности, описанной около правильного треугольника, изображённого на рисунке.

Размер клетки 1х1.

Найдите хорду, на которую опирается угол 30 O , вписанный в окружность радиуса 37.

К окружности, вписанной в треугольник ABC , проведены три касательные. Периметры отсеченных треугольников равны 18, 29, 35.

Найдите периметр данного треугольника.

В треугольнике АВС, АС=20, ВС=4,5 угол С равен 90°. Найдите радиус вписанной окружности .

Катеты равнобедренного прямоугольного треугольника равны 18+9 . Найдите радиус окружности, вписанной в этот треугольник.

В прямоугольный треугольник вписана окружность радиусом 21см. Периметр треугольника равен 228см. Найти радиус описанной окружности.

Точка касания боковой стороны равнобедренного треугольника и вписанной в этот треугольник окружности делит боковую сторону в отношении 15:21, считая от вершины основания треугольника.

Во сколько раз боковая сторона этого треугольника больше его основания?

Краткое описание документа:

Тест по теме «Вписанная окружность в треугольник и описанная окружность около треугольника» составлен для повторения материала и подготовки как к ОГЭ, так и ЕГЭ.

Задачи № 4-6 отрабатывают формулу радиуса окружности, вписанной в прямоугольный треугольник r = (a + b — c ):2. Хотя эти задачи можно решить и другим способом. Тест состоит из 7 задач в трёх вариантах.

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 555 040 материалов в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

§ 4. Вписанная и описанная окружности

Другие материалы

• 28.05.2020
• 88
• 3

• 26.05.2020
• 264
• 2

• 23.01.2020
• 1363
• 53

• 29.11.2019
• 342
• 10

• 05.09.2019
• 305
• 9

• 27.01.2019
• 788
• 12

• 27.01.2019
• 409
• 3

• 06.01.2019
• 404
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 31.05.2020 715
• DOCX 119.1 кбайт
• 37 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Тюлюкина Оксана Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 11 месяцев
• Подписчики: 2
• Всего просмотров: 41068
• Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

В России классы будут переводить на дистант, если заболели 20% детей

Время чтения: 1 минута

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ТЕСТ НА ЭРУДИЦИЮ и кругозор: МНОГО УМНЫХ ВОПРОСОВ, ответы знает не каждый. #насколькотыумный #тестСкачать

Тест: Вписанная и описанная окружности

Вписанная и описанная окружности

В равнобедренном треугольнике точка касания вписанной окружности делит боковую сторону на отрезки длиной 12 см и 3 см, считая от отнования. Найдите площадь треугольника. (в ответе укажите только число без единицы измерения)

Дополните определение:
Если все стороны многоугольника касаются окружности, то окружность называется .

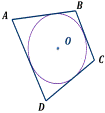
Если около четырехугольника можно описать окружность, то .

Выберите один из 4 вариантов ответа:

1) сумма противоположных углов равна 180 0 .

2) суммы противоположных сторон равны.

3) суммы смежных сторон равны.

4) сумма соседних углов равна 180 0 .

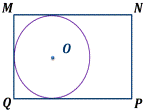
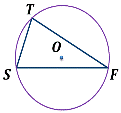
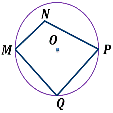
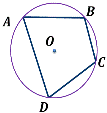
Какие из данных многоугольников описаны около окружности?

Выберите несколько из 3 вариантов ответа:

1)

2)

3)

Найдите стороны остроугольного равнобедренного треугольника, если высота, проведенная к его основанию, равна 8 см, а радиус окружности, в которую он вписан 5 см.

Выберите несколько из 5 вариантов ответа:

1)

2)

Дополните определение:
Если все вершины многоугольника лежат на окружности, то окружность называется .

Окружность можно вписать в любой треугольник?

Выберите один из 5 вариантов ответа:

1) только в равносторонний.

2) в треугольник нельзя вписать окружность.

4) только в равнобедренный.

5) только в прямоугольный.

Если в четырехугольник можно вписать окружность, то .

Выберите один из 4 вариантов ответа:

1) суммы его смежных сторон равны.

2) сумма соседних углов равна 180 0 .

3) сумма противоположных углов равна 180 0 .

4) суммы его противоположных сторон равны.

Выберите верные утверждения:

Выберите несколько из 5 вариантов ответа:

1) Треугольник нельзя описать около окружности.

2) Около квадрата нельзя описать окружность.

3) Прямоугольник нельзя описать около окружности.

4) Около прямоугольника можно описать окружность.

5) Ромб можно описать около окружности.

Какие из данных многоугольников вписаны в окружность?

Выберите несколько из 3 вариантов ответа:

1)

2)

3)

🌟 Видео

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Тема 9. Вписанные и описанные четырехугольникиСкачать

Все о вписанных и описанных окружностях с нуля | PARTAСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

Вписанные и описанные окружности (в треугольник)Скачать

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать

Вписанные четырехугольники. 9 класс.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать