Вокруг треугольника abc описана окружность bc 8

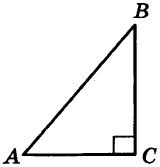
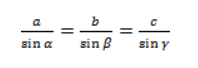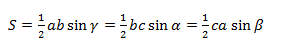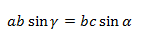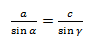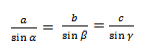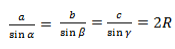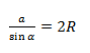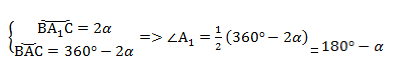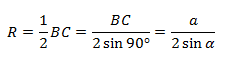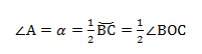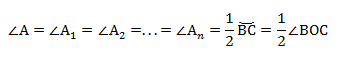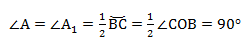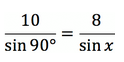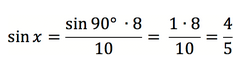В треугольнике АВС известно, что АС = 6, ВС = 8, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.

Источник: ОГЭ Ященко 2022 (50 вар)

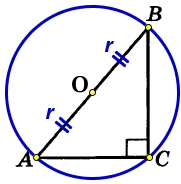
Около прямоугольного треугольника всегда можно описать окружность , при этом гипотенуза будет являться диаметром окружности:

Найдём гипотенузу АВ по теореме Пифагора:

АВ 2 = АС 2 + ВС 2
АВ 2 = 6 2 + 8 2 = 36 + 64 = 100
АВ = √100 = 10

Радиус равен половине диаметра окружности:

r = d/2 = АВ/2 = 10/2 = 5

Ответ: 5.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Видео:№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

Около треугольника ABC описана окружность ; AB = 5, AC = 7, BC = 8?

Геометрия | 5 — 9 классы

Около треугольника ABC описана окружность ; AB = 5, AC = 7, BC = 8.

Чему равно расстояние от точки С до касательной, проходящей через точку А?

(Возможно , решение по теореме : Мера угла между касательной и хордой, имеющими общую точку на окружно — сти, равна половине градусной меры дуги, за — ключённой между его сторонами.

Быстрее будет с этой теоремой.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Угол между двумя секущими проходящими через точку вне окружности, равна 35 градусов?

Угол между двумя секущими проходящими через точку вне окружности, равна 35 градусов.

Градусная мера большей дуги окружности расположенной между сторонами этого угла, равна 100 градусов.

Найдите градусную меру меньшей дуги, находящийся между сторонами данного угла.

Видео:Геометрия Около треугольника ABC описана окружность с центром O и радиусом, равным 8. НайдитеСкачать

СРОЧНО ПЛИЗЗ?

Докажите, что угол между касательной и хордой, имеющими общую точку на окружности, равна половине градусной меры дуги, заключенной между его сторонами.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Диагонали АС и ВD четырехугольника АВCD, вписанного в окружность, пересекаются в точке Р?

Диагонали АС и ВD четырехугольника АВCD, вписанного в окружность, пересекаются в точке Р.

Градусная меря меньшей дуги окружности, стягиваемой хордой ВС, равна 100 градусов , а градусная мера меньшей дуги окружности, стягиваемой хордой АD, равна 150.

Найдите градусную меру угла АРВ .

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, касаются сторон угла с вершиной A?

Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, касаются сторон угла с вершиной A.

Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C.

Найдите радиус окружности, описанной около треугольника ABC.

Видео:Геометрия Вершины равнобедренного треугольника ABC (AB = BC) делят описанную около него окружностьСкачать

Точка А и окружность радиуса 6 см лежат в плоскости, расстояние от точки А до центра окружности равно 12 см?

Точка А и окружность радиуса 6 см лежат в плоскости, расстояние от точки А до центра окружности равно 12 см.

Вычислите градусную меру угла между касательными к окружности, проведёнными через точку А.

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Около треугольника ABC с углами 50° и 66° описана окружность?

Около треугольника ABC с углами 50° и 66° описана окружность.

Найдите углы треугольника, вершинами которого являются точки пересечения касательных к окружности в точках А, В и С.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Ребята, помогите, пожалуйста?

Ребята, помогите, пожалуйста!

))) Две касающиеся внешним образом в точке К окружности, радиусы которых равны 22 и 33, касаются сторон угла с вершиной А.

Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С.

Найдите радиус окружности, описанной около треугольника АВС.

Видео:Построить описанную окружность (Задача 1)Скачать

В окружности с центром в точке О проведена хорда АВ?

В окружности с центром в точке О проведена хорда АВ.

Угол между хордой АВ и касательной к окружности, проходящей через точку В, равен 55 градусов.

Найдите градусную меру центрального угла АОВ.

Покажите рисунок и полное объяснение.

Видео:Задание 24 ОГЭ по математике #7Скачать

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А?

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А.

Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С, Найдите радиус окружности, описанной около треугольника АВС.

Видео:Геометрия Радиус окружности описанной около треугольника ABC равен 6 см Найдите радиус окружностиСкачать

В окружности с центром точке О проведена хорда AB ?

В окружности с центром точке О проведена хорда AB .

Угол между хордой AB и касательной к окружности , проходящей через точку B, равен 55 градусов .

Найдите градусную меру центрального угла AOB.

Вы открыли страницу вопроса Около треугольника ABC описана окружность ; AB = 5, AC = 7, BC = 8?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Пусть меньшая сторона равна х, тогда большая сторона параллелограмма равна х + 4. По условию 4 / 3 = (х + 4) / х. Решаем пропорцию 4х = 3х + 12, х = 12. Одна сторона равна 12 см, другая 12 + 4 = 16 см.

Точкой пересечения биссектрис является центр вписанной в треугольник окружности, то тогда расстояние от О до стороны MN = r. Тогда расстояние от О до стороны NK = MN = 6. S∆NOK = 1 / 2 * 6 * 10 = 30 см².

S одной = 50×50 = 2500см ^ 2 Sзала = 50×2500 = 125000см ^ 2.

Видео:#ОГЭ №15. Задача на #sin. В треугольнике ABC угол C прямой. BC = 8, Sina = 0.4. Найдите AB=?Скачать

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:В треугольнике ABC AC=4, BC=3, угол C равен 90° ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

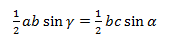
На b сокращаем, синусы переносим в знаменатели:

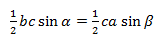
bc sinα = ca sinβ

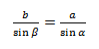
Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

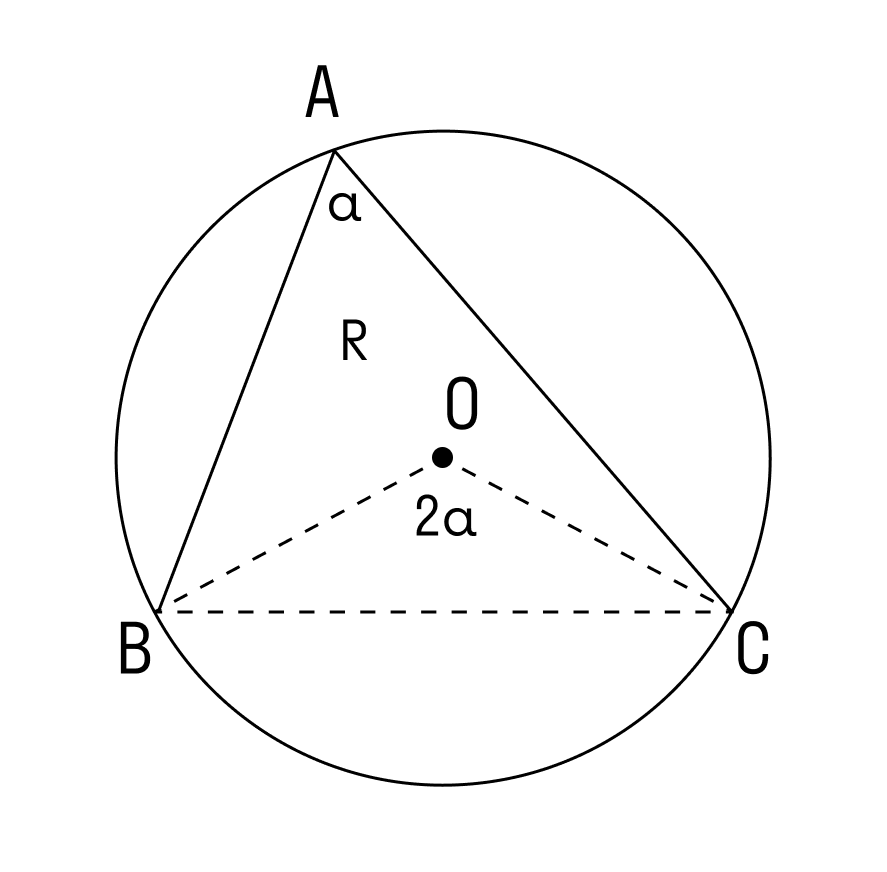
2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° — 60°) = sin60° = 3/√2;
• sin150° = sin(180° — 30°) = sin30° = 1/2;
• sin135° = sin(180° — 45°) = sin45° = 2/√2.

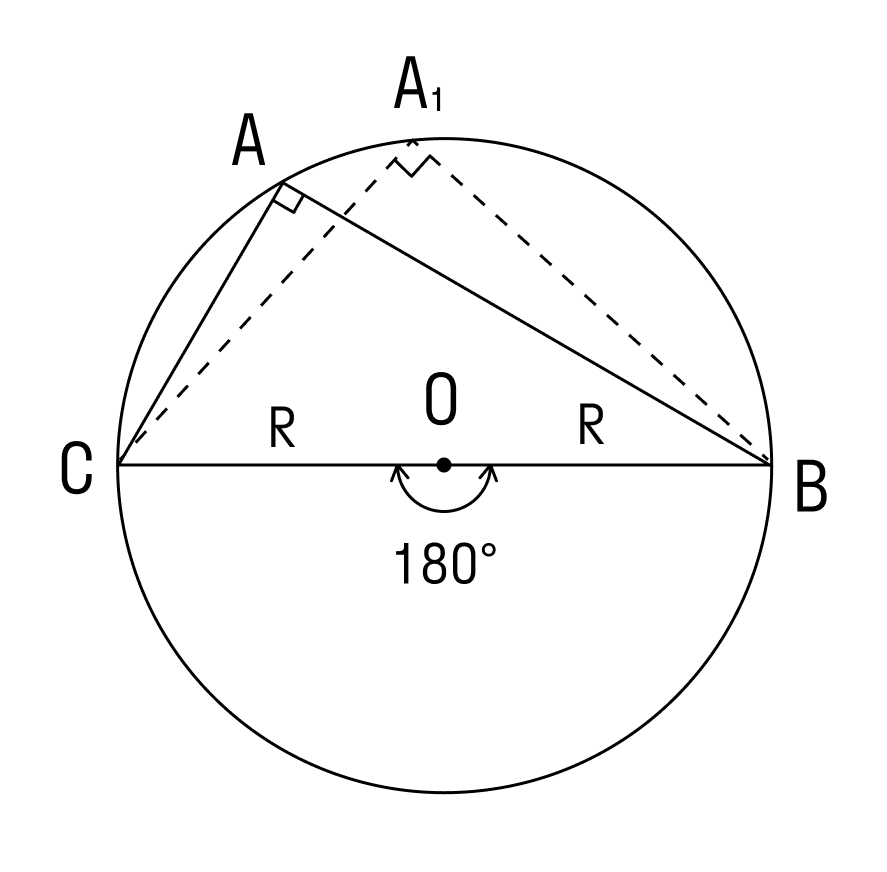
3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Видео:8 класс, 39 урок, Описанная окружностьСкачать

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

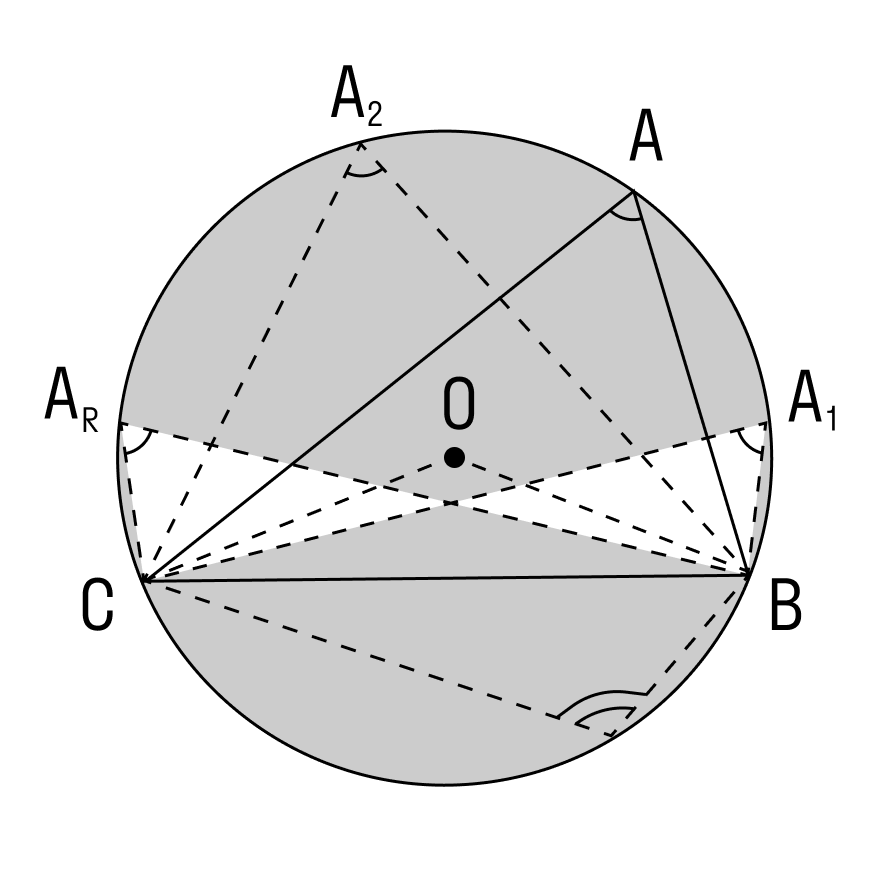
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Видео:№ 301-400 - Геометрия 8 класс МерзлякСкачать

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

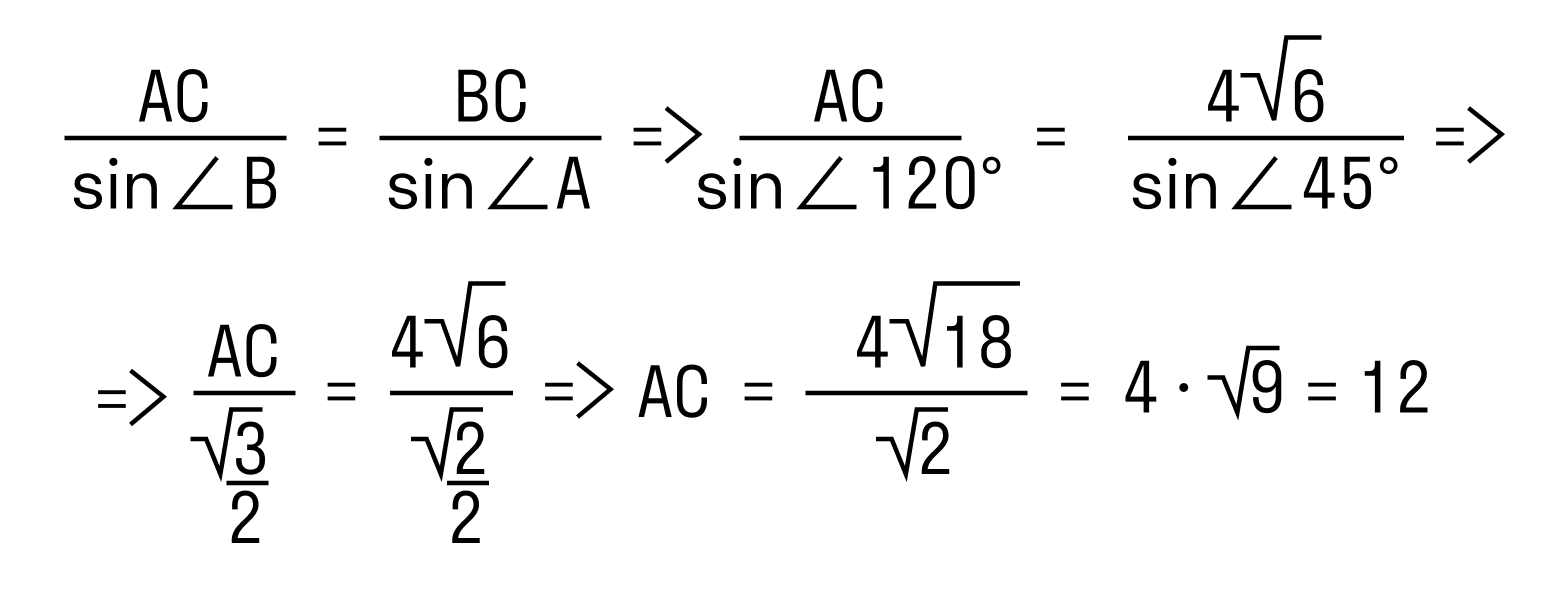
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

📸 Видео

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

№121. В треугольнике ABC дано: ∠C = 90°, AC = 6 см, ВС = 8 см, СМ — медиана. Через вершину ССкачать

В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать