Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, то есть два луча с общим началом называются углом. Лучи, образующие угол, называются сторонами угла, а их общее начало — вершиной угла.
- Обозначение углов
- Внутренняя и внешняя область
- Внутренняя и внешняя область треугольника
- Обозначение угла
- Развернутый угол. Внутренняя и внешняя область угла
- Типы углов
- Сравнение углов
- Градусная мера угла
- Треугольник. Формулы определения и свойства треугольников.
- Определение треугольника
- Классификация треугольников
- 1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
- 2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
- 3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
- 4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
- 5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
- 6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
- Свойства треугольника
- 1.Свойства углов и сторон треугольника.
- 2.Теорема синусов.
- 3. Теорема косинусов.
- 4. Теорема о проекциях
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- 📹 Видео
Видео:Пояснение для областей угла. Внутренняя и внешняя области угла.Скачать

Обозначение углов
Угол обозначается или одной буквой или цифрой, поставленной при вершине угла, например угол A или угол 1, или тремя буквами, из которых одна стоит при его вершине, а две другие при каких-либо точках его сторон. При обозначении угла тремя буквами, буква, стоящая при его вершине, произносится и пишется между двумя другими, например угол AOB. Слово угол в записи заменяют знаком ∠, например ∠1.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Внутренняя и внешняя область
Два луча, исходящие из одной точки, образуют два угла. Для обозначения нужного угла, угол обычно помечается дугой:
Если рассматриваются оба угла, образованные двумя лучами, то они помечаются разным числом дуг, но только в том случае, если углы не равны. Равные углы обозначаются одинаково.
Любой угол делит плоскость на две области. Одна область обычно называется внутренней, а другая внешней. Внутренняя область угла — это часть плоскости, расположенная между сторонами рассматриваемого угла:
Внешняя область угла — это часть плоскости, которая не принадлежит рассматриваемому углу.
Видео:Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

Внутренняя и внешняя область треугольника
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.
Лучи называются сторонами угла, а их общее начало − вершиной угла.
 |
Видео:Измерение угла с помощью транспортираСкачать

Обозначение угла
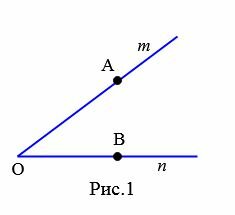
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают ( small ∠mn ) или ( small ∠O. ) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: ( small ∠AOB ) или ( small ∠BOA. )
Видео:Внешний угол треугольникаСкачать

Развернутый угол. Внутренняя и внешняя область угла
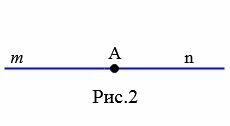
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
 |
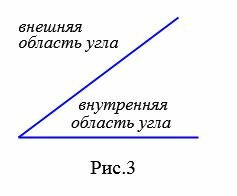
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).
 |
Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
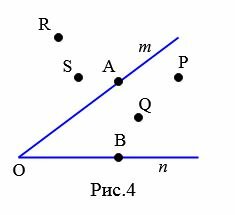
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.
 |
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Типы углов
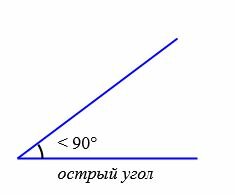
В зависимости от величин, углы бывают следующих типов (Рис.5):
- Нулевой угол (0°). Стороны угла совпадают. Его внутренняя область пустое множество.
- Острый угол (больше 0° и меньше 90°)
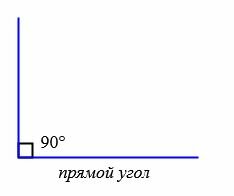
- Прямой угол (90°). Стороны прямого угла перпендикулярны друг другу.
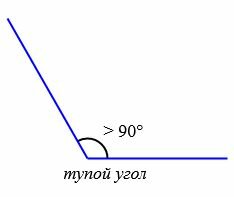
- Тупой угол (больше 90° и меньше 180°).
- Развернутый угол (180°).
- Невыпуклый угол (от 0° до 180° включительно).
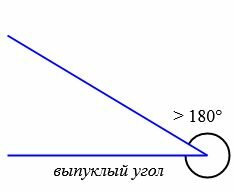
- Выпуклый угол (больше 180° и меньше 360°).
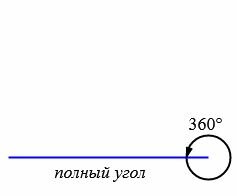
- Польный угол (360°).
  |
  |
  |
Видео:Соотношения между сторонами и углами треугольникаСкачать

Сравнение углов
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.
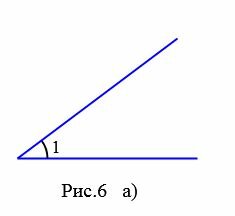 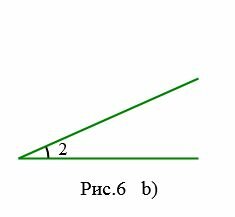 |
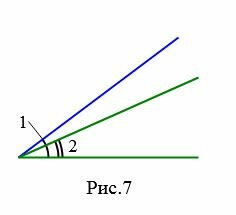
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: ( small ∠2 lt angle 1. )
 |
Видео:Геометрия 7 класс (Урок№2 - Луч и угол.)Скачать

Градусная мера угла
Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является ( small frac ) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
 |
Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: ( small ∠AOB=120 °. ) Очевидно, что градусная мера развернутого угла равна 180°. ( small frac ) часть градуса называется минутой и обозначается так: » ‘ «. ( small frac ) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: ( small angle AOB=56°6’43». )
Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.
Видео:Топография паховой области и пахового треугольникаСкачать

Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Видео:Найти площадь треугольника АВС. Задачи по рисункамСкачать

Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Видео:Окружность. 7 класс.Скачать

Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
📹 Видео
ОГЭ Задание 25 Свойство ортоцентраСкачать

Задание 9 Площадь треугольникаСкачать

Окружности касаются внешне и теорема Пифагора. Внешняя и внутренняя касательные, секущая. ЕГЭ, ОГЭ.Скачать
Задание 25 Первый и второй признаки подобияСкачать

Математика 5 класс (Урок№28 - Треугольники.)Скачать

Найти угол между биссектрисой и высотойСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать














