Теорема. Сумма внутренних углов треугольника равна двум прямым углам.
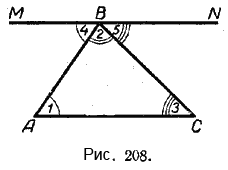
Возьмём какой-нибудь треугольник AВС (рис. 208). Обозначим его внутренние углы цифрами 1, 2 и 3. Докажем, что
Проведём через какую-нибудь вершину треугольника, например В, прямую МN параллельно АС.
При вершине В мы получили три угла: ∠4, ∠2 и ∠5. Их сумма составляет развёрнутый угол, следовательно, она равна 180°:
Но ∠4 = ∠1 — это внутренние накрест лежащие углы при параллельных прямых МN и АС и секущей АВ.
∠5 = ∠3 — это внутренние накрест лежащие углы при параллельных прямых МN и АС и секущей ВС.
Значит, ∠4 и ∠5 можно заменить равными им ∠1 и ∠3.
Следовательно, ∠1 + ∠2 + ∠3 = 180°. Теорема доказана.
- 2. Свойство внешнего угла треугольника.
- 3. Свойство прямоугольного треугольника с углом в 30°.
- Треугольник. Сумма внутренних углов треугольника.
- / 1 + / 2 + / 3 = 2 d . = 180 0 .
- Внутренние односторонние углы — теория, правило и свойства
- Углы по определению
- Доказательство теоремы
- Следствие из свойства прямых
- Построение параллелограмма
- 🎬 Видео
2. Свойство внешнего угла треугольника.
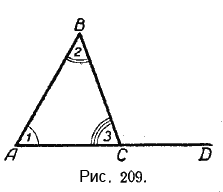
В самом деле, в треугольнике ABC (рис. 209) ∠1 + ∠2 = 180° — ∠3, но и ∠ВСD, внешний угол этого треугольника, не смежный с ∠1 и ∠2, также равен 180° — ∠3.
Следовательно, ∠1 + ∠2= ∠BCD.
Выведенное свойство внешнего угла треугольника уточняет содержание ранее доказанной теоремы о внешнем угле треугольника, в которой утверждалось только, что внешний угол треугольника больше каждого внутреннего угла треугольника, не смежного с ним; теперь же устанавливается, что внешний угол равен сумме обоих внутренних углов, не смежных с ним.
3. Свойство прямоугольного треугольника с углом в 30°.
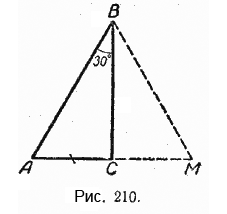
Пусть в прямоугольном треугольнике АСВ угол В равен 30° (рис. 210). Тогда другой его острый угол будет равен 60°.
Докажем, что катет АС равен половине гипотенузы АВ. Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ, равный отрезку АС. Точку М соединим с точкой В. Полученный треугольник ВСМ равен треугольнику АСВ. Мы видим, что каждый угол треугольника АВМ равен 60°, следовательно, этот треугольник — равносторонний.
Катет АС равен половине АМ, а так как АМ равняется АВ, то катет АС будет равен половине гипотенузы АВ.
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Треугольник. Сумма внутренних углов треугольника.
Сумма внутренних углов треугольника равняется 180 0 .
Начертим какой — либо треугольник AВС. Отметим его внутренние углы как 1, 2 и 3. Необходимо обосновать, что:
Видео:№224. Найдите углы треугольника ABC, если ∠A:∠B:∠C= 2:3:4.Скачать

/ 1 + / 2 + / 3 = 2 d . = 180 0 .
Прочертим через любую вершину треугольника, к примеру В, прямую МN параллельную АС.
При вершине В сформировались углы: / 4, / 2 и / 5. Все вмести они образуют развёрнутый угол, логично, что их сумма она равняется 2d:
Учитывая, что / 4 = / 1 — это внутренние накрест расположенные углы сформированные параллельными прямыми МN и АС и секущей АВ.
/ 5 = / 3 — это внутренние накрест расположенные углы сформированные параллельными прямыми МN и АС и секущей ВС.
Следовательно, / 4 и / 5 можно поменять на одинаковые — / 1 и / 3.
И тогда, / 1 + / 2 + / 3 = 2 d либо 180°. Теорема обоснованна.
Видео:Внешний угол треугольникаСкачать

Внутренние односторонние углы — теория, правило и свойства
Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих. Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.
Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Доказательство теоремы
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.
Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Видео:№223. Найдите угол С треугольника ABC, если: a) ∠A=65°, ∠B = 57°; б) ∠A = 24°, ∠B= 130Скачать
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:
Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
Видео:№1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать

Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.
Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:
Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.
🎬 Видео
Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

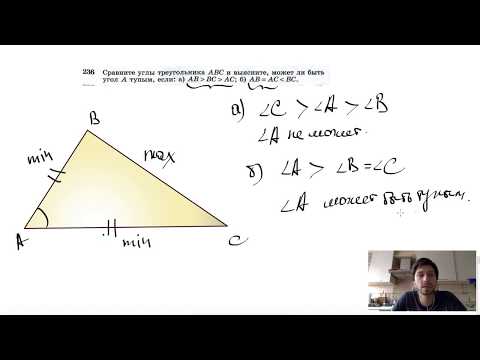
№236. Сравните углы треугольника ABC и выясните, может ли быть угол А тупым, если: а) АВСкачать
Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

ВНЕШНИЕ УГЛЫ ТРЕУГОЛЬНИКА 😉 #shorts #математика #егэ #огэ #профильныйегэСкачать

Математика ОГЭ и ЕГЭ Внутренние, внешние углы треугольникаСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Геометрия. 7 класс. Сумма углов треугольника. Внешний угол треугольника /28.01.2021/Скачать

Внешний угол треугольникаСкачать

Задачи по рисункам. Найти углы треугольника АВС. Сумма углов треугольника.Скачать
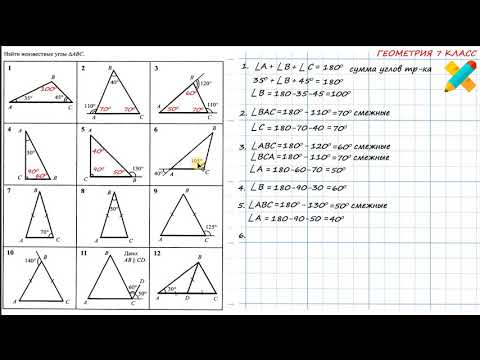
В треугольнике ABC углы А,В и С относятся как 1 :1:7 .Найти углы треугольника ABC.7 кл.ОгэСкачать

Вычисляем угол через координаты вершинСкачать

7 класс. Внешний угол треугольника.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать