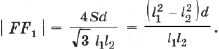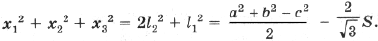Некоторые малоизвестные факты из геометрии треугольника
Некоторые малоизвестные факты из геометрии треугольника Статья представляет собой дополнение к очень популярной теме «Геометрия треугольника». В ней рассматриваются некоторые известные факты с оригинальными авторскими доказательствами. Некоторые пункты можно разобрать дополнительно к отдельным темам: вписанная окружность, теорема Пифагора, векторный метод, точка Ферма, треугольники Наполеона. В конце каждого пункта приводятся упражнения, позволяющие закрепить рассматриваемые темы, уяснить их с разных сторон. Во многих случаях сами упражнения содержат важный теоретический материал. Многие упражнения взяты из известных учебников.
1. Симметричный вывод формулы Герона
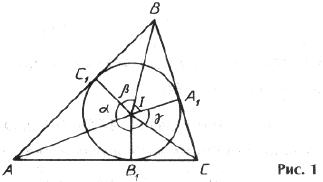
Точки касания вписанной окружности со сторонами треугольника обозначим через A1, B1, C1 (рис. 1). Треугольники AIB1 и AIC1, BIA1 и BIC1, CIA1 и CIB1 попарно равны, как прямоугольные треугольники, имеющие общую гипотенузу и равные углы.
откуда AB1 = AC1 = 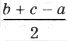
Аналогично CA1 = CB1 =
и BA1 = BC1 = 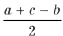
Обозначим углы Р C1IB1 = a , Р C1IA1 = b , Р A1IB1 = g . В D AIB1 катеты связаны соотношением
откуда
.
Аналогично
.
Так как
,
то легко доказать
(*)
Подставив в (*) выражения
через a, b, c и r, получим
= ,
откуда
Так как SABC = rp, то отсюда следует формула Герона.
.
Здесь и далее через R обозначен радиус описанной окружности.
3. Докажите, что в D ABC биссектриса угла A, средняя линия, параллельная AC, и прямая, соединяющая точки касания вписанной окружности со сторонами CB и CA, пересекаются в одной точке.
4. Докажите, что сумма квадратов расстояний от точек касания вписанной в треугольник окружности с его сторонами до центра описанной равна 3R 2 – 4Rr – r 2 .
5. Центр окружности, вписанной в прямоугольный треугольник, находится на расстоянии и см от концов гипотенузы. Найдите катеты этого треугольника.
6. В D ABC известно BC = a, Р A = a , Р B = b . Найдите радиус окружности, пересекающей все его стороны и высекающей на каждой из них хорды длины d.
7. В D ABC проведена медиана AM. Может ли радиус окружности, вписанной в D ABM, быть ровно в два раза больше радиуса окружности, вписанной в D ACM?
8*. Окружность, вписанная в D ABC, делит медиану BM на три равные части. Найдите отношение BC : CA : AB.
2. К теореме Пифагора
Многие доказательства теоремы Пифагора используют характерный рисунок квадратов, построенных во внешнюю стороны на сторонах треугольника («Пифагоровы штаны»).
Доказательство сводится к доказательству формулы
где S – площадь квадрата, построенного на гипотенузе, S1, S2 – площади квадратов, построенных на катетах.
Обычно при этом используется разбиение квадратов на равные части, совмещающиеся друг с другом.
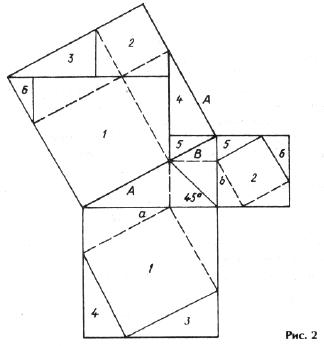
Минимальное число фигур разбиения – 5 (Ан-Нариций, древнеиндийское «колесо с лопастями»), бывает 7 и 8). На рис. 2 показано разбиение, в котором совмещается 6 фигур.
Биссектриса прямого угла исходного треугольника делит гипотенузу на части длиной A и B, причем по свойству биссектрисы A : B = a : b, где a и b – длины катетов.
Проведем в квадрате, построенном на гипотенузе, штриховые линии на расстоянии A и B от сторон. Рассмотрим выделенный жирным контуром прямоугольный треугольник. Он подобен исходному, так как его катеты A и B пропорциональны a и b. Поэтому гипотенуза выделенного треугольника параллельна катету b, так как соответствующие накрест лежащие углы равны. Теперь можно провести остальные линии разбиения: в квадрате, построенном на гипотенузе, – параллельно катетам, а в квадратах, построенных на катетах, – параллельно сторонам квадрата, построенного на гипотенузе (причем во втором случае длины отрезков разбиения равны A и B). Нетрудно видеть, что при этом получаются совмещающиеся фигуры.
1. Высота, опущенная на гипотенузу, делит прямоугольный треугольник на два, подобных исходному. Пользуясь тем, что площади подобных фигур относятся как квадраты их линейных элементов, докажите теорему Пифагора (Ч. Тригг).
2. Впишем в прямоугольный треугольник окружность, которая точками касания делит катеты на отрезки, два из которых по длине совпадают с r – радиусом окружности. Пользуясь результатами п. 1, еще раз докажите теорему Пифагора (доказательство Мёльманна).
3. Точки O1, O2, O3 – соответственно центры квадратов, построенных на катете и гипотенузе, C – вершина прямого угла исходного треугольника. Докажите, что отрезки O1O2 и O3C перпендикулярны, а их длины равны.
4. Найдите площадь O1O2O3 (см. упражнение 3), если длины катетов прямоугольного треугольника равны a и b.
3. Теорема Лейбница
Если O – точка пересечения медиан D ABC, P – произвольная точка плоскости, то (рис. 3)
Доказательство. Возведем векторное равенство
Аналогично получаются равенства:
Складывая эти три равенства, получаем
так как сумма векторов в скобках равна нулю. Отсюда
Так как
то отсюда следует доказываемая формула.
Дополнительное упражнение. Получите формулы для медиан треугольника
1. Докажите, что сумма квадратов расстояний от произвольной точки плоскости до вершины треугольника является минимальной, если точка совпадает с точкой пересечения медиан.
2. Вычислите расстояние от точки пересечения медиан до центра описанной окружности.
3. Вычислите расстояние от точки пересечения медиан до центра вписанной окружности.
4. Докажите, что для произвольной точки P, лежащей на окружности, вписанной в равносторонний D ABC,
PA 2 + PB 2 + PC 2 = const.
5. Полупериметр D ABC равен p. Докажите, что для любой точки M плоскости имеет место неравенство
причем равенство достигается лишь в случае, когда ABC – правильный треугольник и M – его центр.
6*. Радиус круга, описанного около треугольника, равен R. Расстояние от центра этого круга до точки пересечения медиан треугольника равно d. Найдите произведение площади данного треугольника и треугольника, образованного прямыми, проходящими через его вершины перпендикулярно медианам, из этих вершин выходящим. Указание. Если O – точка пересечения медиан исходного D ABC, то отрезки OA, OB, OC делят второй больший треугольник на 3 вписанных четырехугольника, площади которых можно выразить через стороны и площади треугольников AOB, AOC, BOC, а, значит, – ABC.
7*. Пусть ABC – правильный треугольник со стороной a, M – некоторая точка плоскости, находящаяся на расстоянии d от центра треугольника ABC. Докажите, что площадь треугольника, стороны которого равны отрезкам MA, MB и MC, выражается формулой
Точкой Ферма называется такая точка треугольника, сумма расстояний от которой до вершин треугольника является минимальной. Когда все углы треугольника меньше 120°, то точка Ферма – это такая точка F в треугольнике, из которой все стороны треугольника видны под одним и тем же углом 120°.
Доказательство. Проведем через вершины исходного D ABC прямые, перпендикулярные отрезкам AF, BF и CF соответственно. Они пересекутся в вершинах некоторого правильного треугольника A1B1C1. Для любой точки P D A1B1C1 сумма длин перпендикуляров, опущенных из P на стороны этого треугольника, есть постоянное число (в частности, оно равно AF + BF + CF), так как она равна , где S – площадь A1B1C1, a – его сторона. Очевидно, что PA не меньше длины перпендикуляра, опущенного из P на сторону B1C1, проходящую через A. Тем более, PA + PB + PC не меньше суммы длин всех перпендикуляров, которая равна AF + BF + CF, и равенство достигается, когда P совпадает с F.
Иногда точку Ферма называют точкой Торичелли или точкой Брокара.
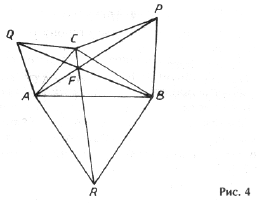
Чтобы построить точку Ферма, надо на сторонах D ABC во внешнюю сторону построить равносторонние треугольники ABR, BCP и ACQ. Отрезки AP, BQ и CR пересекаются в точке F – точке Ферма (рис. 4).
Действительно, пусть AP и BQ пересекаются в точке F. При повороте вокруг точки C на 60° D CQB переходит в D CAP. Следовательно, угол между QB и AP Р QFA = 60°, и точка F лежит на окружности, описанной около D AQC. Аналогично угол Р PFB = 60°, и точка F лежит на окружности, описанной около D BPC. Так как угол Р AFB = 120°, то точка F лежит на окружности, описанной около D ABR, значит, Р AFR = 60°. Так как при повороте на 60° вокруг точки B D APB переходит в D RCB, то угол между AP и CR равен 60° и точка F лежит на CR.
1. Используя теорему Птолемея для четырехугольника AFBR и обозначив расстояния от F до вершин D ABC через x1, x2, x3, найдите AP = BQ = CR (рис. 4).
5. Треугольники Наполеона
Если на сторонах D ABC внешним образом построить равносторонние треугольники, то их центры являются вершинами равностороннего внешнего треугольника Наполеона.
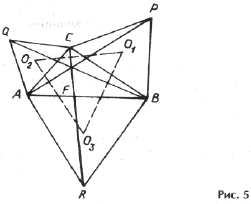
Действительно, вершины D O1O2O3 являются центрами окружностей, описанных вокруг равносторонних треугольников и пересекающихся в точке F. Поэтому стороны D O1O2O3 перпендикулярны отрезкам FA, FB и FC, и углы между ними равны 60° (рис. 5).
Если на сторонах D ABC построить равносторонние треугольники во внутреннюю сторону и соединить их центры, то получится равносторонний внутренний треугольник Наполеона.
Применив теорему косинусов к D CO1O2, можно вывести формулу для стороны внешнего треугольника Наполеона:
где S – площадь D ABC.
Для стороны внутреннего треугольника Наполеона аналогично получается
1. Докажите, что центры треугольников Наполеона совпадают с точкой пересечения медиан (для этого вычислите расстояние от какой-нибудь вершины треугольника Наполеона до точки пересечения медиан и покажите, что оно на зависит от рассматриваемой величины и равно

где l – длина стороны треугольника Наполеона).2. Докажите, что разность площадей треугольников Наполеона (внешнего и внутреннего) равна площади D ABC.
3. Докажите, что
4. Применив теорему Лейбница для внешнего треугольника Наполеона и точки Ферма F, вычислите расстояние от точки пересечения медиан, которая является центром треугольника Наполеона, до точки Ферма.
5. Докажите, что
6. Докажите, что PQ 2 + QR 2 + RP 2 = a 2 + b 2 + c 2 + 9l1 2 .
7. Докажите, что точка пересечения медиан D PQR совпадает с точкой G пересечения медиан D ABC.
Указание. Вычислите длины PG, QG, RG и примените теорему Лейбница; второй способ – докажите, что векторная сумма
8. На сторонах треугольника во внешнюю сторону построены квадраты. Докажите, что точка пересечения медиан треугольника с вершинами в центрах этих квадратов совпадает с точкой пересечения медиан данного треугольника.
(См. указание к упр. 7, второй способ.)
9. Рассмотрим центроиды A1, B1, C1 треугольников AQR, BPR и CQP соответственно. Докажите, что D A1B1C1 – правильный и центр его совпадает с центроидом G данного D ABC.
Указание. Докажите, что равны векторы
10. Докажите, что треугольники A1B1C1 и O1O2O3 симметричны относительно их общего центра G и поэтому шестиугольник O1C1O2A1O3B1 – правильный и его центр совпадает с центроидом G данного треугольника. Сторона этого шестиугольника
.
11. Докажите, что середины A2, B2, C2 отрезков AO1, BO2, CO3 являются вершинами еще одного равностороннего треугольника он гомотетичен внутреннему треугольнику Наполеона с
.
12*. Пусть A3, B3, C3 – середины отрезков QR, PR и QP соответственно. Докажите, что прямые AA3, BB3, CC3 пересекаются в одной точке или параллельны.
13. Докажите, что если подобные треугольники PCB, CQA, BAR построены извне на сторонах произвольного D ABC, то окружности, описанные вокруг этих трех треугольников, имеют общую точку.
14. Докажите, что в условиях упражнения 13 центры трех указанных окружностей образуют треугольник, подобный треугольникам PCB, CQA, BAR.
15. Докажите, что если на двух сторонах треугольника построены квадраты, то окружности, описанные вокруг них, пересекаются на окружности, построенной на третьей стороне, как на диаметре, и центры этих трех окружностей являются вершинами равнобедренного прямоугольного треугольника.
16. Докажите, что прямые AO1, BO2, CO3 пересекаются в одной точке (см. рис. 5).
Указание. Продолжить эти прямые до пересечения со сторонами треугольника ABC и применить теорему Чевы.
6. Расстояние от точки Ферма до центра описанной окружности
Ранее было получено, что
где
l1 – длина стороны внешнего треугольника Наполеона (упражнения 4.1, 4.2 и 5.5).
•. (1)
Точка Ферма F лежит на прямой CC1, которая соединяет вершину C исходного D ABC с вершиной C1 равностороннего D ABC1 (рис. 6); O – центр описанной окружности.
Обозначим угол BCC1 через j ;

С учетом этого преобразуем формулу (2):
Найдем по теореме косинусов для D BCC1
Для a (применим теоремы косинусов и синусов к D ABC)
Подставив полученные выражения в (3), находим
Тогда с учетом (1) получим
(4)
(5)
которую преобразуем к виду
(6)
где d – расстояние от точки пересечения медиан до центра описанной окружности.
Дополнение: точка F1 пересечения прямых AP ‘, BO ‘ и CR ‘, где ABR ‘, BCP ‘ и ACO ‘ – равносторонние треугольники, построенные на сторонах D ABC во внутреннюю сторону, является точкой, двойственной точке Ферма. Точка F1 лежит на окружности, описанной около внешнего треугольника Наполеона. Расстояние между точками F и F1 равно (без доказательства)
1. Докажите, что расстояние от точки Ферма F до центра описанной окружности O больше расстояния от точки пересечения медиан G до центра описанной окружности O.
2. Вычислите угол Р OGF в обозначениях упражнения 1 и формулы (6).
3. Доказать, что
4*. Точка F – точка Ферма D ABC (углы которого меньше 120°). Докажите, что прямые Эйлера треугольников AFB, BFC и CFA пересекаются в одной точке.
Содержание
- math4school.ru
- Теорема Наполеона, и не только
- Теорема Наполеона
- Теорема Петра-Дугласа-Неймана
- Первая теорема Тебо
- Теорема ван Обеля
- На сторонах треугольника ABC внешним образом построены правильные треугольники ABC1, AB1C и A1BC. Пусть P и Q — середины отрезков A1B1 и A1C1. Докажите, что треугольник APQ правильный.
- 📸 Видео
Видео:Строим треугольник по трем сторонам (Задача 5).Скачать
math4school.ru
Видео:Построение треугольника по двум сторонам и углу между ними. 7 класс. Геометрия.Скачать
Теорема Наполеона, и не только
Известно, что Наполеон Бонапарт (1769–1821) увлекался математикой, больше всего – геометрией. В частности, известен его способ деления окружности на четыре равные части с помощью только циркуля. Будучи политическим деятелем, Наполеон всегда высоко ставил роль науки и учёных в строительстве государственности. Так о математике он говорил:
Процветание и совершенство математики тесно связаны с благосостоянием государства.
Как-то Наполеон, который тогда еще не был правителем Франции, спорил с известными математиками Лагранжем и Лапласом. Во время одной из дискуссий Лаплас прервал Наполеона словами:
Меньше всего мы желаем, чтоб вы, генерал, учили нас геометрии!
Интересно, что в дальнейшем Лаплас стал главным военным министром Наполеона.
Теорема Наполеона
Теорема, о которой пойдёт речь впервые была опубликована английским математиком Уильямом Резерфордом (1798–1871) в 1825 году, спустя 4 года после смерти Наполеона. Хотя Наполеон и занимался геометрией достаточно серьёзно и небезуспешно, как для непрофессионального математика, многие специалисты сомневаются в том, что он является автором теоремы, названной его именем. А теперь к сути.
Если на сторонах треугольника построить правильные треугольники, то получим конфигурацию из четырех треугольников, которую называют треугольниками Наполеона . Окружности, описанные вокруг построенных правильных треугольников, называют окружностями Торричелли .
Именно Наполеону Бонапарту – императору Франции и великому полководцу – история приписывает изучение этой конфигурации, формулировку и доказательство утверждения, известного как теорема Наполеона :
Если на сторонах произвольного треугольника извне его построены равносторонние треугольники, то их центры являются вершинами равностороннего треугольника .
В различных источниках приводятся разные доказательства теоремы Наполеона. Чаще всего можно встретить доказательства, основанные на свойствах поворота или использующие комплексные числа. С одним из элементарных доказательств, основанном на применении теоремы косинусов, можно познакомиться на сайте «Математика, которая мне нравится». Мы докажем теорему Наполеона, используя свойства окружности.
Пусть на сторонах треугольника АВС построены равносторонние треугольники АВС 1, А 1 ВС и АВ 1 С ; ω 1, ω 2 и ω 3 – окружности, описаны вокруг этих треугольников (соответственно). Докажем, что ω 1, ω 2 и ω 3 пересекаются в одной точке – точке Торричелли .
Обозначим точку пересечения окружностей, описанных вокруг треугольников А 1 ВС и АВ 1 С , как М . Тогда
∠АМС = 180° – 60° = ∠ВМС .
∠АМВ = 360° – 2 · 120° = 120°,
и точка М лежит на окружности, описанной вокруг АВС 1. Прямые О 1 О 3 и О 1 О 2 перпендикулярны к общим хордам АМ и ВМ окружностей ω 1 и ω 3, ω 1 и ω 2 соответственно.
Аналогично: ∠О 2 = ∠О 3 = 60°, и треугольник О 1 О 2 О 3 – правильный. Теорема Наполеона доказана.
Мы строили правильные треугольники извне заданного треугольника на его сторонах. Их ещё называют внешними треугольниками Наполеона для заданного треугольника. По аналогии, если правильные треугольники строят на сторонах треугольника внутрь его, то их называют внутренними треугольниками Наполеона для заданного треугольника. Треугольник с вершинами в центрах внутренних треугольников Наполеона также является правильным.
Теорема Петра-Дугласа-Неймана
Теорема Наполеона обобщается на случай произвольных треугольников теоремой Петра-Дугласа-Неймана :
Если подобные треугольники любой формы построены на сторонах треугольника внешним образом так, что каждый повёрнут относительно предыдущего, и три соответствующие точки этих треугольников соединены, то итоговый треугольник будет подобен этим внешним треугольникам.
Первая теорема Тебо
Аналогом теоремы Наполеона для параллелограммов является утверждение называемое первой теоремой Тебо :
Центры квадратов, построенных на сторонах параллелограмма, лежат в вершинах квадрата.
Теорема ван Обеля
Следует, пожалуй, упомянуть ещё один математический факт, опубликованный фламандским математиком ван Обелем (Henricus Hubertus van Aubel) в 1878 году, из которого теорема Тебо следует естественным образом:
Если на сторонах произвольного несамопересекающегося четырёхугольника построить квадраты внешним образом и соединить центры противоположных, то полученные отрезки будут равны и перпендикулярны.
Источники: Г.В. Апостолова. Геометрия 8 (Киев, «Генеза», 2008), Википедия.
Видео:Построение треугольника по углу и двум сторонам. 7 класс.Скачать
На сторонах треугольника ABC внешним образом построены правильные треугольники ABC1, AB1C и A1BC. Пусть P и Q — середины отрезков A1B1 и A1C1. Докажите, что треугольник APQ правильный.
При повороте на 60 o относительно точки A, переводящем точку C в точку B1, равносторонний треугольник A1BC переходит в равносторонний треугольник A2MB1. Поэтому
При рассматриваемом повороте отрезок C1A1 переходит в отрезок BA2. Поэтому середина Q отрезка C1A1 переходит в середину P отрезка BA2. Следовательно, треугольник APQ — равносторонний.
📸 Видео
Внешний угол треугольникаСкачать
Геометрия - Построение правильного треугольникаСкачать
Построение треугольника, равного данномуСкачать
7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать
Построение треугольника по трем сторонам. 7 класс.Скачать
Построение треугольника по трем сторонам. 7 класс . Геометрия.Скачать
Построение треугольника по стороне и двум прилежащим к ней углам. 7 класс. Геометрия.Скачать
Построение равностронего треугольника.Скачать
№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать
Строим треугольник по стороне и двум углам (Задача 7).Скачать
ВНЕШНИЕ УГЛЫ ТРЕУГОЛЬНИКА 😉 #shorts #математика #егэ #огэ #профильныйегэСкачать
Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать
Решить за 45 минут Классная задача на построениеСкачать
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать
Построение медианы в треугольникеСкачать
Строим вписанную в данный треугольник окружность (Задача 2).Скачать
Внешний угол треугольникаСкачать
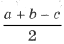
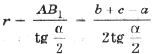
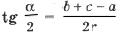 .
.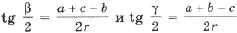 .
.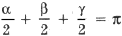 ,
,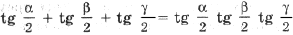 (*)
(*)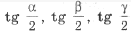
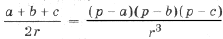 = ,
= ,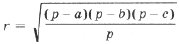
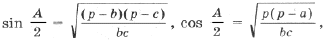
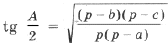 .
.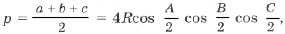
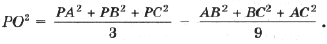

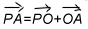
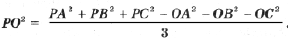
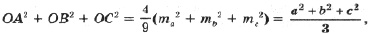
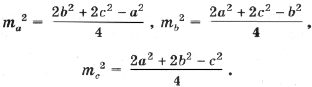
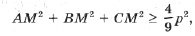
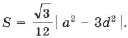
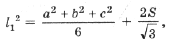
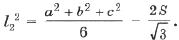
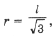
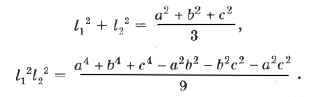
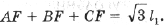
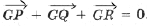
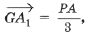
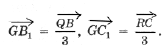
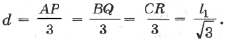 .
. .
.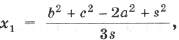
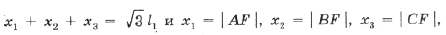

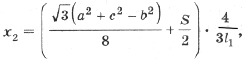
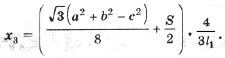 •. (1)
•. (1)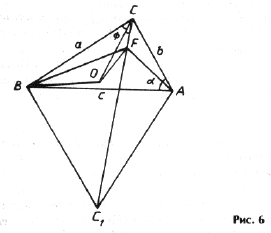
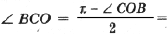
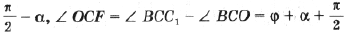
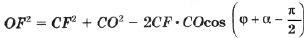
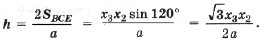
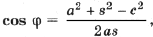
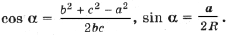
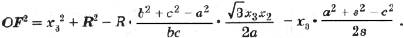
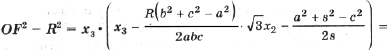
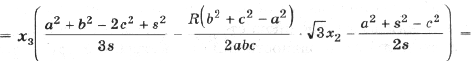
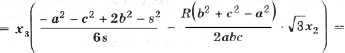
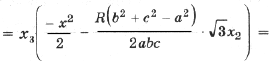
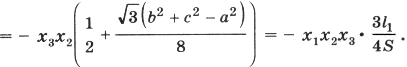
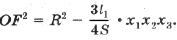 (4)
(4)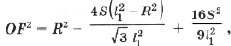 (5)
(5)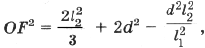 (6)
(6)