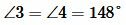Вертикальные углы в равнобедренном треугольнике (3 видео)

Вертикальные углы. Свойства вертикальных углов

Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

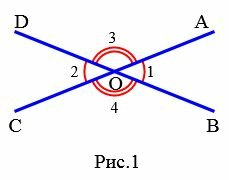Вертикальные углы в равнобедренном треугольнике

На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Содержание

Свойства вертикальных углов
Задачи и решения
Вертикальные углы
Вертикальные углы в равнобедренном треугольнике
Виды углов. Измерение углов
Смежные и вертикальные углы
Свойства смежных и вертикальных углов
Углы при пересечении двух прямых секущей
📹 Видео

Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

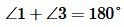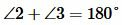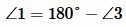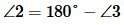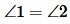
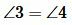
Следовательно . Аналогично доказывается, что .

Видео:Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.Скачать

Задачи и решения

Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

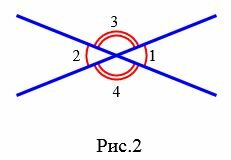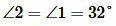
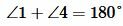
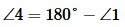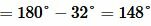Решение. Так как углы 1 и 2 вертикальны, то . Углы 1 и 4 смежные. Следовательно . Тогда

Углы 3 и 4 вертикальные. Тогда

Ответ. .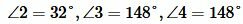

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

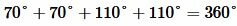Ответ. .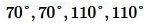

Видео:Вертикальные углы. 7 класс.Скачать

Вертикальные углы

Какие углы вертикальные? Каким свойством обладают вертикальные углы?

Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.

Определение.

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.

При пересечении двух прямых образуется две пары вертикальных углов:

∠1 и ∠2 — вертикальные углы

∠3 и ∠4 — вертикальные углы

Свойство вертикальных углов.

Вертикальные углы равны.

Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.

1) Сумма вертикальных углов равна 140º. Найти эти углы.

Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.

2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.

При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.

Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.

А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.

Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.

Видео:Смежные углы. 7 класс.Скачать

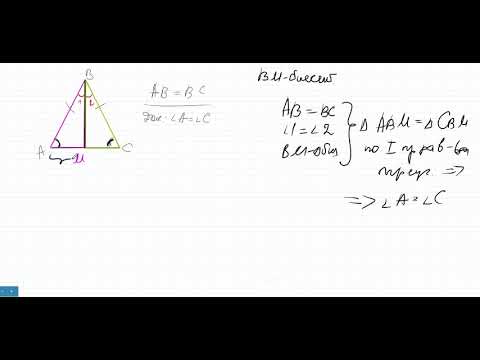
Вертикальные углы в равнобедренном треугольнике

Ключевые слова конспекта: углы, биссектриса, виды углов, измерение углов, смежные и вертикальные углы, свойства смежных и вертикальных углов, углы при пересечении двух прямых секущей.

Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины).
Биссектриса — луч, который выходит из вершины угла и делит его пополам.

Виды углов. Измерение углов

Развернутый угол — угoл, стороны которого лежат на одной прямой.
Прямой угoл — угoл, который равен половине развернутого угла.
Острый угол — угoл меньше прямого угла.
Тупой угoл — угoл больше прямого, но меньше развернутого.

Единицы измерения углов:
Градус — величина (градусная мера) угла, равная части развернутого угла.
Минута — часть градуса.
Секунда — часть минуты.

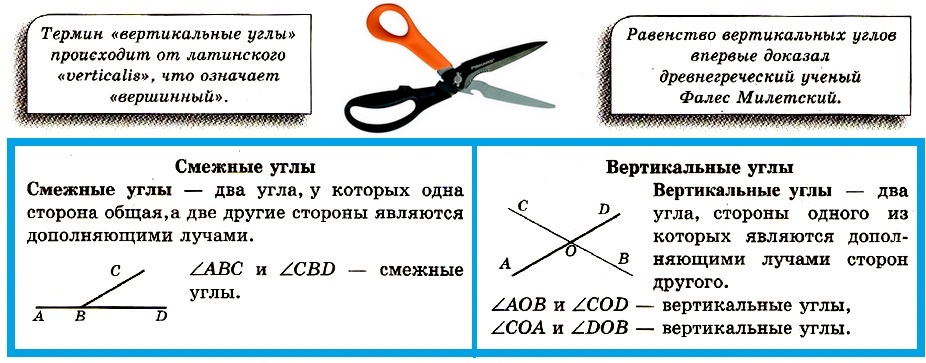
Смежные и вертикальные углы

Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого.

Теорема. Сумма смежных углов равна 180°.

Теорема. Вертикальные углы равны.

Свойства смежных и вертикальных углов

Углы при пересечении двух прямых секущей

Вы смотрели конспект по геометрии «Угол. Смежные и вертикальные углы». Использованы цитаты из учебных пособий:

Цитирование указанных пособий произведено в учебных целях (часть 1 статьи 1274 Гражданского кодекса РФ) с указанием авторства, источника заимствования и ссылки на покупку учебного пособия в крупнейшем книжном Интернет-магазине. Выберите дальнейшие действия: