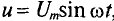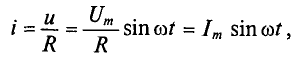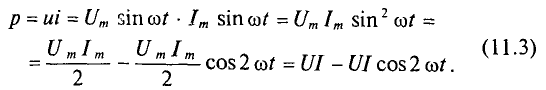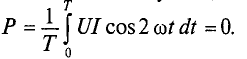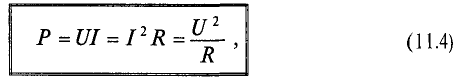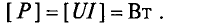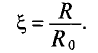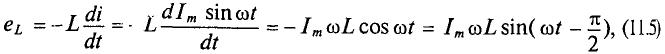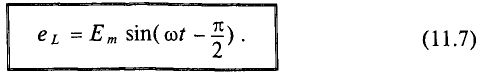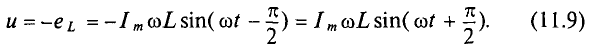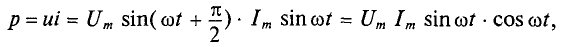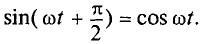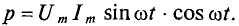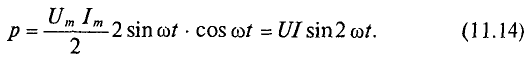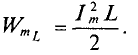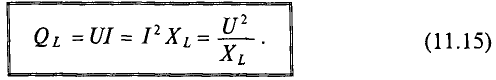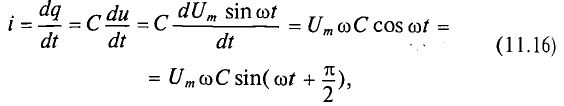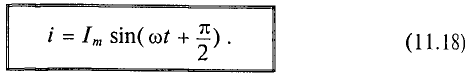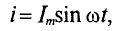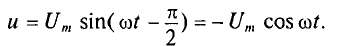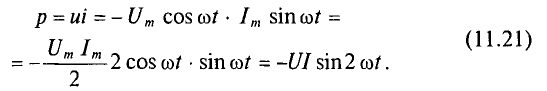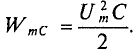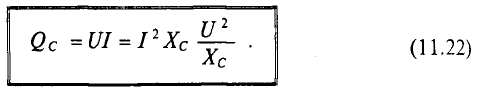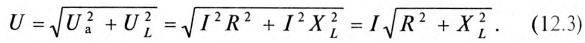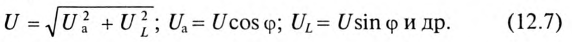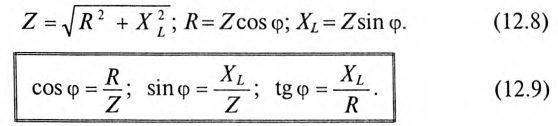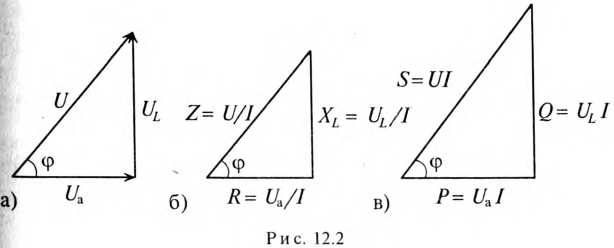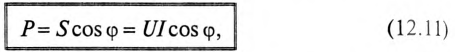Векторная диаграмма треугольники сопротивлений

Содержание:

Схема цепи с последовательным соединением элементов

В общем случае любое реальное устройство, содержащееся в электрической цепи, может быть представлено в схеме замещения тремя идеальными элементами. Поэтому целесообразно при анализе цепей синусоидального тока знать соотношение тока и напряжения для участка цепи с тремя последовательно соединенными элементами: резистором, идеальным индуктивным и идеальным емкостным элементами.

Схема замещения такой неразветвленной цепи показана на рис. 23.

Рис. 23. Схема цепи с последовательным соединением элементов R, L, С.

Под действием синусоидального напряжения в цепи возникает синусоидальный ток . Необходимо определить соотношение между синусоидальными током и напряжением этой цепи по величине и по фазе.

Синусоидальный ток с амплитудой и начальной фазой , изображается в виде:

или в комплексной форме:

По второму закону Кирхгофа для контура рассматриваемой цепи полное напряжение цепи соотносится с напряжениями на отдельных элементах в виде:

Как показано ранее (51), (71), (90), напряжение на каждом из элементов соотносятся с током в соответствии с законом Ома:

Ток во всех элементах при их последовательном соединении одни и тот же. Тогда выражение (98) может быть представлено в виде:

или

Здесь

— комплексное полное сопротивление цепи с тремя последовательно соединенными элементами.

Таким образом выражение (103) определяет соотношение между комплексным током и комплексным напряжением также в форме закона Ома: комплексный ток в цепи с тремя последовательно соединенными элементами прямо пропорционален комплексному напряжению и обратно пропорционален комплексному полному сопротивлению этой цепи.

Возможно вам будут полезны данные страницы:

Модуль и аргумент комплексного полного сопротивления определяются параметрами отдельных элементов.

Исходя из (104), модуль комплексного полного сопротивления

где — реактивное сопротивление цепи.

Аргумент комплексного полного сопротивления

В соответствии с законом Ома в комплексном виде для этой цепи (103),

Исходя из полученного выражения (107), действующее значение тока

начальная фаза тока

или

Как видно, действующие значения тока и напряжения в этой цепи также определяется полным сопротивлением Z в форме закона Ома. По фазе напряжение опережает ток на угол . При этом полное сопротивление и разность фаз определяются соотношением сопротивлений трех элементов в соответствии выражениями (105) и (106).

Тот же результат может быть получен посредством наглядного графического изображения тока и напряжений на векторной диаграмме.

Векторная диаграмма

Векторная диаграмма для рассматриваемой цепи показана на рис. 24.

Здесь начальная фаза тока принята произвольно равной нулю . При этом вектор тока направлен вдоль вещественной оси комплексной плоскости.

Рис. 24. Векторная диаграмма цепи с последовательным соединением элементов L, R, С.

Вектор напряжения индуктивного элемента повернут относительно вектора тока на в сторону опережения в соответствии со свойствами этого элемента (66). Вектор напряжения резистора направлен вдоль вектора тока в соответствии с характеристиками резистора (47). Вектор напряжения емкостного элемента повернут на угол относительно вектора тока в сторону отставания в соответствии со свойствами емкостного элемента (85). Длина векторов напряжений определяется их действующими значениями по закону Ома для каждого из элементов в соответствии с (67), (46), (83).

Соотношение напряжений по второму закону Кирхгофа (98) на векторной диаграмме соответствует векторному сложению. При этом вектор полного напряжения цепи на рис. 24 определяется суммой трех векторов напряжений на отдельных элементах:

Из построенной векторной диаграммы возможен анализ соотношения тока и полного напряжения цепи. Для этого выделим на векторной диаграмме прямоугольный треугольник ОАВ (рис. 25).

Треугольник напряжений цепи с последовательным соединением элементов

Треугольник напряжений цепи с последовательным соединением элементов. Обозначить ОАВ

Нижний катет треугольника пропорционален напряжению резистора, которое определяется его активным сопротивлением, и его называют активной составляющей напряжения . Правый катет треугольника пропорционален разности напряжений двух реактивных элементов: индуктивного и емкостного, и его называют реактивной составляющей напряжения:

Гипотенуза треугольника пропорциональна величине полного напряжения цепи U. Угол определяет разность фаз всей цепи.

Этот треугольник называют треугольником напряжений и используют для наглядного представления соотношения между отдельными составляющими напряжений при анализе цепи с последовательным соединением R,L,C -элементов.

Поделим стороны треугольника напряжений на величину тока . При этом получается подобный треугольник (рис. 26) со сторонами:

Рис. 26. Треугольник сопротивлений цепи с последовательным соединением элементов.

— активное сопротивление резистора;

— реактивное сопротивление, определяемое разностью индуктивного и емкостного сопротивлений;

— полное сопротивление цепи, определяющее соотношение по величине тока и полного напряжения.

Угол определяет разность фаз всей цепи.

Этот треугольник называют треугольником сопротивлений и используют для наглядного представления соотношения между сопротивлениями отдельных элементов и полным сопротивлением цепи с последовательным соединением R,L,C — элементов.

По теореме Пифагора для треугольника сопротивлений модуль полного сопротивления

Он определяет соотношение по величине между током и полным напряжением.

Из того же треугольника разность фаз для всей цепи

Она описывает соотношение по фазе между током и полным напряжением и определяет аргумент комплексного полного сопротивления.

Таким образом, комплексное полное сопротивление может быть записано в виде:

Оно определяет соотношение между током и напряжением по закону Ома в комплексном виде:

При этом модуль комплексного полного сопротивления Z определяет соотношение по величине действующих значений напряжения и тока: , а аргумент комплексного сопротивления определяет соотношение синусоидальных напряжения и тока по фазе:

Полученные при графическом анализе выражения (112) — (115) соответствуют записанным ранее (105) — (107).

Эти выражения справедливы для цепи, содержащей в общем случае три идеальных элемента, соединенные последовательно. В частности, реальное устройство может быть представлено эквивалентной схемой с двумя или одним идеальным элементом. В этом случае полученное выражение также верно. Следует лишь формально принять сопротивление отсутствующего элемента равным нулю.

Пример задачи с решением

Для цепи на рис. 21 определить напряжение источника, используя понятие полного комплексного сопротивления.

Рассматривая эту цепь как частный случай цепи с тремя идеальными элементами, можно принять емкостное сопротивление равным нулю . При этом комплексное полное сопротивление

Напряжение всего участка по закону Ома в комплексном виде:

Аналогичным образом можно определять комплексное полное сопротивление участка цепи, содержащего два других идеальных элемента, или один из них.

Используя графические изображения в форме треугольников напряжений и сопротивлений, можно записать выражения, полезные при расчете и анализе такой электрической цепи:

Для анализа энергетических соотношений в цепи с последовательным соединением R, L, С — элементов определим характер изменения мгновенной мощности в этой цепи:

Или, используя действующие значения тока и напряжения,

Как видно из полученного выражения (121), мощность в рассматриваемой цепи изменяется во времени по гармоническому закону с двойной частотой. При этом колебания мощности происходят вокруг среднего значения, определяемого первым слагаемым в правой части этого выражения.

Среднее значение мощности определяет активную мощность. Тогда активная мощность

или

Как видно, активная мощность определяется мощностью резистора. Произведение действующих значений тока и полного напряжения цепи называют полной мощностью

Единица полной мощности — ВА, кВА, МВА.

Исходя из (123 ) и (124) соотношение активной и полной мощностей:

, или

Активная мощность определяет необратимое преобразование электрической энергии в другие виды энергии, т.с. полезную работу, совершаемую током в электрической цепи. В общем случае активная мощность является частью общего значения тока и определяется произведением текущего значения тока на общее напряжение. Этот процент активной мощности определяется по уравнению (125). Отношение активной мощности к полной называется коэффициентом мощности. Принимая во внимание выражение (125), коэффициент мощности обозначают

Коэффициент мощности можно определить соотношением сопротивлений отдельных элементов, например, исходя из треугольника сопротивлений (рис. 26):

Графически соотношение активной и полной мощности отображается треугольником мощностей. Для построения треугольника мощностей умножим треугольник напряжений на действующее значение тока. При этом образуется подобный прямоугольный треугольник (рис. 27).

Рис. 27. Треугольник мощностей цепи с последовательным соединением элементов.

Нижний катет треугольника пропорционален активной мощности:

Правый катет треугольника пропорционален величине:

Это реактивная мощность всей цепи.

Гипотенуза треугольника оказывается равной полной мощности:

Из треугольника мощностей:

или

Что соответствует полученным ранее выражениям.

При выполнении расчетов в комплексном виде комплексное значение полной мощности определяется произведением комплексного напряжения на сопряженный комплексный ток:

Здесь сопряженный комплексный ток. Тогда:

В рассматриваемой цепи с последовательным соединением R, L, С — элементов при разном соотношении сопротивлений элементов создается разный режим работы. При этом характер цепи определяется разностью фаз (/>, значения которой могут быть положительными или отрицательными в диапазоне от

Ниже рассматриваются режимы работы цепи при разных соотношениях индуктивного и емкостного сопротивлений.

Показанная на рис. 24 векторная диаграмма построена в предположении, что индуктивное сопротивление больше емкостного . Реактивное сопротивление всей цепи положительно:

При этом в соответствии с законом Ома напряжение на индуктивном элементе больше емкостного:

Разность фаз всей цепи оказывается положительной, т.е. полное напряжение опережает по фазе ток на угол , больший нуля:

Треугольник сопротивлений и треугольник мощностей для этого режима имеют вид, показанный на рис. 26,27.

В этом режиме цепь характеризуется активной мощностью Р и положительной реактивной мощностью Положительное значение реактивной мощности свидетельствует о том, что индуктивная мощность больше емкостной, т.е. индуктивный элемент преобладает над емкостным элементом.

В этом режиме характер цепи называют активно-индуктивным.

При сопротивлении индуктивного элемента, меньшим емкостного,

При этом в соответствии с законом Ома напряжение на индуктивном элементе меньше емкостного:

Векторная диаграмма для этого режима показана на рис. 28.

Рис. 28. Векторная диаграмма неразветвленной цепи при

Разность фаз всей цепи оказывается отрицательной, т.е. полное напряжение отстает по фазе от тока:

Треугольник сопротивлений и треугольник мощностей для этого режима показаны на рис. 29.

Рис. 29. Треугольник сопротивлений и треугольник мощностей при

В этом режиме цепь характеризуется активной мощностью Р и отрицательной реактивной мощностью Отрицательное значение реактивной мощности свидетельствует о том, что индуктивная мощность меньше емкостной, т.е. емкостный элемент преобладает над индуктивным элементом.

В этом режиме характер цепи называют активно-емкостным.

Особый режим работы цепи возникает при равенстве индуктивного и емкостного сопротивлений:

Реактивное сопротивление всей цепи оказывается равным нулю:

При этом в соответствии с законом Ома напряжения на индуктивном и емкостном элементах равны между собой:

а реактивное напряжение равно нулю:

Векторная диаграмма для этого режима показана на рис. 30.

Рис. 30. Векторная диаграмма неразветвленной цепи при

Разность фаз всей цепи оказывается равной нулю, т.е. полное напряжение совпадает по фазе с током:

Треугольник сопротивлений и треугольник мощностей для этого режима вырождаются в отрезок, поскольку один катет становится равным нулю.

В этом режиме цепь характеризуется активной мощностью Р . Реактивная мощность равна нулю . При этом активная мощность равна полной мощности:

а коэффициент мощности равен

Отсутствие реактивной мощности при наличии в цепи индуктивного и емкостного элементов свидетельствует о том, что реактивная индуктивная мощность и реактивная емкостная мощность взаимно компенсируются. При этом цепь имеет активный характер, поскольку обладает лишь активной мощностью.

Явление, возникающее в неразветвленной цепи с элементами L, R, С, когда полное напряжение и ток совпадают по фазе, называется резонансом напряжений.

Условие резонанса напряжений:

Создать резонанс напряжений в цепи можно изменяя параметры L или С при неизменной частоте, или изменяя частоту при заданных параметрах L и С.

Рассмотрим случай, когда £ и С неизменны при изменении частоты. На рис. 31 показаны зависимости сопротивлений и тока цепи от частоты

Рис. 31. Зависимости от частоты.

В точке . При этом полное сопротивление минимально и определяется лишь активным сопротивлением резистора:

Эта точка определяет резонансную частоту

Ток цепи в этом режиме наибольший:

Активная мощность определяется величиной резонансного тока:

Аналогичным образом возникает режим резонанс напряжений при неизменной частоте и изменении индуктивности индуктивного элемента, либо емкости емкостного элемента. При установлении равенства индуктивного и емкостного сопротивлений возникает резонанс напряжений. При этом полное сопротивление цепи минимально, а ток максимальный.

Признаком резонанса напряжений в цепи является максимальное значение тока и активной мощности

Резонанс напряжений используется в радиотехнических цепях при построении схем резонансных фильтров. При этом свойства цепи оказываются различными для сигналов разных частот.

В электротехнических установках частота неизменна. Здесь возникновение резонанса напряжений обусловлено изменением параметров элементов. При при резонансе напряжений возможны перенапряжения на отдельных участках цепи.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Откуда взялась формула полного сопротивления цепи? Треугольник напряжений, треугольник сопротивленийСкачать

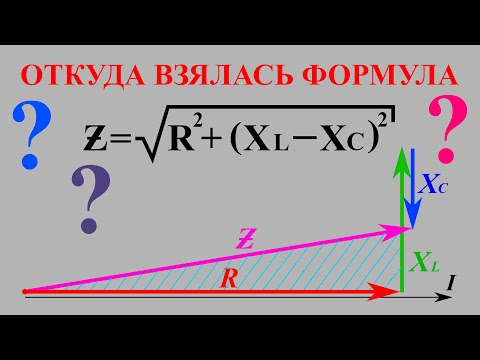
Треугольники напряжений, сопротивлений и мощностей

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Звезда и треугольник принцип подключения. Особенности и работа

Для увеличения мощности передачи без увеличения напряжения сети, снижения пульсаций напряжения в блоках питания, для уменьшения числа проводов при подключении нагрузки к питанию, применяют различные схемы соединения обмоток источников питания и потребителей (звезда и треугольник).

Схемы

Обмотки генераторов и приемников при работе с 3-фазными сетями могут соединяться с помощью двух схем: звезды и треугольника. Такие схемы имеют между собой несколько отличий, различаются также нагрузкой по току. Поэтому, перед подключением электрических машин необходимо выяснить разницу в этих двух схемах — звезда и треугольник.

Схема звезды

Соединение различных обмоток по схеме звезды предполагает их подключение в одной точке, которая называется нулевой (нейтральной), и имеет обозначение на схемах «О», либо х, у, z. Нулевая точка может иметь соединение с нулевой точкой источника питания, но не во всех случаях такое соединение имеется. Если такое соединение есть, то такая система считается 4-проводной, а если нет такого соединения, то 3-проводной.

Схема треугольника

При такой схеме концы обмоток не объединяются в одну точку, а соединяются с другой обмоткой. То есть, получается схема, похожая по виду на треугольник, и соединение обмоток в ней идет последовательно друг с другом. Нужно отметить отличие от схемы звезды в том, что в схеме треугольника система бывает только 3-проводной, так как общая точка отсутствует.

В схеме треугольника при отключенной нагрузке и симметричной ЭДС равно 0.

Фазные и линейные величины

В 3-фазных сетях питания имеется два вида тока и напряжения – это фазные и линейные. Фазное напряжение – это его величина между концом и началом фазы приемника. Фазный ток протекает в одной фазе приемника.

При применении схемы звезды фазными напряжениями являются Ua, Ub, Uc, а фазными токами являются I a, I b, I c. При применении схемы треугольника для обмоток нагрузки или генератора фазные напряжения — Uaв, Ubс, Ucа, фазные токи – I ac, I bс, I cа.

Линейные значения напряжения измеряются между началами фаз или между линейных проводников. Линейный ток протекает в проводниках между источником питания и нагрузкой.

В случае схемы звезды линейные токи равны фазным, а линейные напряжения равны U ab, Ubc, U ca. В схеме треугольника получается все наоборот – фазные и линейные напряжения равны, а линейные токи равны I a, I b, I c.

Большое значение уделяется направлению ЭДС напряжений и токов при анализе и расчете 3-фазных цепей, так как его направление влияет на соотношение между векторами на диаграмме.

Особенности схем

Между этими схемами есть существенная разница. Давайте разберемся, для чего в различных электроустановках используют разные схемы, и в чем их особенности.

Во время пуска электрического мотора ток запуска имеет повышенную величину, которая больше его номинального значения в несколько раз. Если это механизм с низкой мощностью, то защита может и не сработать. При включении мощного электромотора защита обязательно сработает, отключит питание, что обусловит на некоторое время падение напряжения и перегорание предохранителей, или отключение электрических автоматов. Электродвигатель будет работать с малой скоростью, которая меньше номинальной.

Видно, что имеется немало проблем, возникающих из-за большого пускового тока. Необходимо каким-либо образом снижать его величину.

Для этого можно применить некоторые методы:

• Подключить на запуск электродвигателя реостат, дроссель, либо трансформатор.
• Изменить вид соединения обмоток ротора электродвигателя.

В промышленности в основном применяют второй способ, так как он наиболее простой и дает высокую эффективность. Здесь работает принцип переключения обмоток электромотора на такие схемы, как звезда и треугольник. То есть, при запуске мотора его обмотки имеют соединение «звезда», после набора эксплуатационных оборотов, схема соединения изменяется на «треугольник». Этот процесс переключения в промышленных условиях научились автоматизировать.

В электромоторах целесообразно применение сразу двух схем — звезда и треугольник. К нулевой точке необходимо подключить нейтраль источника питания, так как во время использования таких схем возникает повышенная вероятность перекоса фазных амплитуд. Нейтраль источника компенсирует эту асимметрию, которая возникает вследствие разных индуктивных сопротивлений обмоток статора.

Достоинства схем

Соединение по схеме звезды имеются важные преимущества:

• Плавный пуск электрического мотора.
• Позволяет функционировать электродвигателю с заявленной номинальной мощностью, соответствующей паспорту.
• Электродвигатель будет иметь нормальный рабочий режим при различных ситуациях: при высоких кратковременных перегрузках, при длительных незначительных перегрузках.
• При эксплуатации корпус электродвигателя не перегреется.

Основным достоинством схемы треугольника является получение от электродвигателя наибольшей возможной мощности работы. Целесообразно поддерживать режимы эксплуатации по паспорту двигателя. При исследовании электромоторов со схемой треугольника выяснилось, что его мощность повышается в 3 раза, по сравнению со схемой звезды.

При рассмотрении генераторов, схемы – звезда и треугольник по параметрам аналогичны при функционировании электродвигателей. Выходное напряжение генератора будет больше в схеме треугольника, чем в схеме звезды. Однако, при повышении напряжения снижается сила тока, так как по закону Ома эти параметры обратно пропорциональны друг другу.

Поэтому можно сделать вывод, что при разных соединениях концов обмоток генератора можно получить два разных номинала напряжения. В современных мощных электромоторах при запуске схемы – звезда и треугольник переключаются автоматически, так как это позволяет снизить нагрузку по току, возникающей при пуске мотора.

Видео:Построение векторной диаграммы. Цепь RLCСкачать

Соединение приемников энергии треугольником

При соединении приемников энергии треугольником (рис. 6-11) каждая фаза приемника присоединяется к линейным проводам, т. е. включается на линейное напряжение, которое одновременно будет и фазным напряжением приемника:

Таким образом, изменение сопротивления фаз не влияет на фазные напряжения.

Направления линейных токов от генератора к приемнику примем за положительные (рис. 6-11). Направления фазных токов от А’

Согласно первому правилу Кирхгофа для мгновенных значений токов для узла А’

Аналогично для узла В’:

. Соединение приемников треугольником

Следовательно, мгновенное значение любого линейного тока равно алгебраической разности мгновенных значений токов тех фаз, которые соединены с данным проводом.

Векторная диаграмма при соединении приемников треугольником.

Вектор любого линейного тока находится как разность векторов соответствующих фазных токов:

На рис. 6-12 дана векторная диаграмма для трехфазной цепи при соединении приемников энергии треугольником. На этой диаграмме все векторы проведены из одного начала. На рис. 6-13 дана вторая диаграмма для той же цепи, на которой векторы напряжений образуют треугольник, а вектор каждого фазного тока проведен из одного начала с вектором соответствующего фазного напряжения.

Векторная диаграмма при соединении приемников треугольником.

Если при симметричной системе линейных напряжений нагрузка фаз равномерная, т. е.

то действующие значения фазных токов равны между собой и они сдвинуты по фазам на одинаковые углы от соответствующих напряжений (рис. 6-14) и, следовательно, на углы 120° один относительно другого. Следовательно, фазные токи представляют симметричную систему. Симметричную систему будут представлять и линейные токи (рис. 6-14).

Восстановив перпендикуляр из середины вектора линейного тока, например IА,

получим прямоугольный треугольник
OHM,
из которого следует, что

Таким образом, при соединении приемников треугольником при равномерной нагрузке фаз линейные токи больше фазных в √3 раз.

Кроме того, из той же векторной диаграммы следует, что линейные токи отстают от соответствующих фазных токов на углы 30°.

Векторная диаграмма для цепи, соединенной треугольником при равномерной нагрузке фаз.

При соединении приемников треугольником при равно мерной нагрузке фаз расчет трехфазной цепи сводится к расчету одной фазы.

во фазного напряжения определяются из выражений

Активная мощность одной фазы

Реактивная мощность трех фаз

Полная мощность трехфазной цепи

При неравномерной нагрузке фаз мощность трехфазной цепи о пределяется как сумма мощностей отдельных фаз.

Если приемники энергии соединены звездой и за положительное направление линейных токов вобрано направление от генератора к потребителю, то согласно первому правилу Кирхгофа для нейтральной точки можно написать:

Если приемники энергии соединены треугольником, то сумма линейных токов

Следовательно, при любом способе соединения приемников алгебраическая сумма мгновенных значений линейных токов трехфазной трехпроводной цепи равна нулю.

Поэтому, например, намагничивающая сила трех жил трехфазного кабеля равна нулю и, следовательно, не происходит намагничивания стальной брони кабеля, применяемой для защиты от механических повреждений.

Видео:Как построить векторную диаграмму напряжений?Скачать

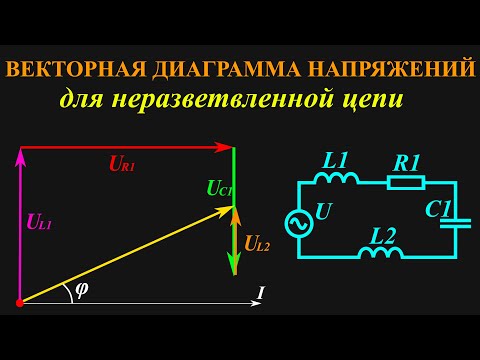
Что такое реактивная мощность?

Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.

Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.

При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.

На индуктивных и ёмкостных нагрузках часть электроэнергии рассеивается в виде тепла, а часть препятствует выполнению полезной работы.

К устройствам с индуктивными нагрузками относятся:

• электромоторы;
• дроссели;
• трансформаторы;
• электромагнитные реле и другие устройства, содержащие обмотки.

Видео:Векторная диаграмма для трехфазной цепи │ТРЕУГОЛЬНИКСкачать

ВКЛЮЧЕНИЕ ПРИЕМНИКОВ ЭНЕРГИИ В СЕТЬ ТРЕХФАЗНОГО ТОКА

Электрические лампы изготовляются на номинальные напряжения 127 и 220 в, а трехфазные электродвигатели на номинальные фазные напряжения 127, 220 и 380 в

Способ включения приемника в сеть трехфазного тока зависит от линейного напряжения сети и от номинального напряжения приемника.

Лампы с номинальным напряжением 127 в

включаются треугольником при линейном напряжении сети 127
в
и звездой с нейтральным проводом при линейном напряжений сета 220
в.
Лампы с номинальным напряжением 220
в
включаются треугольником в сеть с линейным напряжением 220
в
и звездой с нейтральным проводом в сеть с линейным напряжением 380
в.
Трехфазный электродвигатель включается треугольником в сеть, линейное напряжение которой равно номинальному фазному напряжению электродвигателя. Если линейное напряжение сети превышает в √3 раз номинальное фазное напряжение электродвигателя, то он включается звездой.

Статья на тему Соединение приемников энергии треугольником

Видео:R, L, C в цепи переменного тока/Треугольник сопротивлений/Сдвиг по фазеСкачать

Способы компенсации

Мы уже выяснили, как влияют реактивные токи на работу устройств и оборудования с индуктивными или ёмкостными нагрузками. Для уменьшения потерь в электрических сетях с синусоидальным током их оборудуют дополнительными устройствами компенсации.

Принцип действия установок компенсации основан на свойствах индуктивностей и ёмкостей по сдвигу фаз в противоположные стороны. Например, если обмотка электромотора сдвигает фазу на угол φ, то этот сдвиг можно компенсировать конденсатором соответствующей ёмкости, который сдвигает фазу на величину – φ. Тогда результирующий сдвиг будет равняться нулю.

На практике компенсирующие устройства подключают параллельно нагрузкам. Чаще всего они состоят из блоков конденсаторов большой ёмкости, расположенных в отдельных шкафах. Одна из таких конденсаторных установок изображена на рисунке 3. На картинке видно группы конденсаторов, используемых для компенсации сдвигов напряжений в различных устройствах с индуктивными обмотками.

Компенсацию реактивной мощности ёмкостными нагрузками хорошо иллюстрируют графики на рисунке 4. Обратите внимание на то, как эффективность компенсации зависит от напряжения сети. Чем выше сетевое напряжение, тем сложнее компенсировать паразитные токи (график 3).

Устройства компенсации часто устанавливаются в производственных цехах, где работает много устройств на электроприводах. Потери электричества при этом довольно ощутимы, а качество тока сильно ухудшается. Конденсаторные установки успешно решают подобные проблемы.

Видео:Векторные диаграммы и коэффициент мощностиСкачать

Соединение обмоток трансформатора в звезду

При соединении в звезду действуют следующие соотношения –

• линейные токи равны фазным,
• линейные напряжения больше фазных в √3 раз

Возможно множество вариантов соединения обмоток трансформатора в звезду, некоторые из них приведены на рисунке ниже. И, как говорится, не все из них одинаково полезны, а точнее, для разных случаев необходима разная схема соединений.

Следует отметить, что в звезду можно соединить как один трехфазный трансформатор, так и три однофазных. На рисунке обозначаются:

• А, В, С – начала обмоток высшего напряжения
• Х, Y, Z – окончания обмоток высшего напряжения
• a, b, c – начала обмоток низкого напряжения
• x, y, z – окончания обмоток низкого напряжения

Видео:Векторная диаграмма токов и топографическая диаграмма напряженийСкачать

Что такое реактивная мощность и как её рассчитать?

Многие потребители электроэнергии не подозревают того, что часть учтённого электричества расходуется бесполезно. В зависимости от вида нагрузки уровень потерь электроэнергии может достигать от 12 до 50%. При этом счетчики электроэнергии засчитывают эти потери, относя их к полезной работе, за что приходится платить. Виной завышения оплаты за потребление электроэнергии, не выполняющей полезной работы, является реактивная мощность, присутствующая в сетях переменных токов.

Чтобы понять, за что мы переплачиваем и как компенсировать влияние реактивных мощностей на работу электрических установок, рассмотрим причину появления реактивной составляющей при передаче электроэнергии. Для этого придётся разобраться в физике процесса, связанного с переменным напряжением.

Видео:Как снять векторную диаграммуСкачать

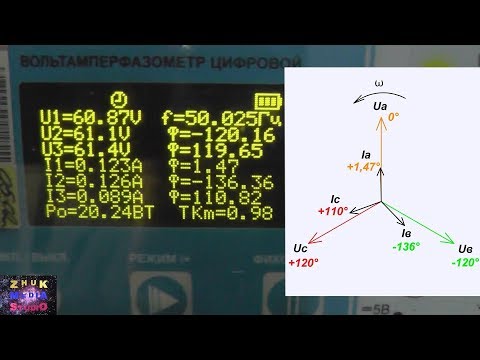
Соединение обмоток трансформатора в треугольник

Соединение в треугольник так называется из-за внешнего сходства с треугольником (видно на рисунке).

При соединении в треугольник действуют следующие соотношения –

• линейные токи больше фазных в √3 раз
• линейные напряжения равны фазным

Три вторичные обмотки, при соединении в треугольник соединены последовательно, образуя тем самым замкнутую цепь. В этой цепи отсутствует ток, так-как ЭДС фаз сдвинуты на 120 градусов и их сумма в каждый момент времени равна нулю. Так же ток равен нулю при соблюдении тотчасно следующих условий – ЭДС имеют синусоидальную форму, обмотки имеют одинаковые числа витков.

Звезда и треугольник в вопросе о третьих гармониках трансформаторов

В трансформаторах схему треугольник используют кроме прочего для получения токов третьих гармоник, которые необходимы для создания синусоидальной ЭДС вторичных обмоток. Другими словами, для исключения третьей гармонической составляющей в магнитном потоке.

Чтобы ввести третьи гармоники при соединении в звезду – соединяют нейтраль звезды с нейтралью генератора, по этому пути и начинают пробегать третьи гармоники.

Видео:Векторная диаграмма при соединении приемника треугольникомСкачать

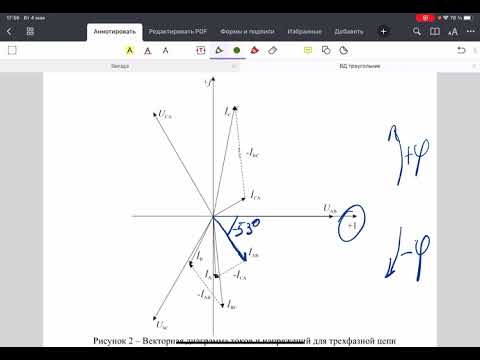
Соединение обмоток трансформатора в зигзаг

Соединение в зигзаг используется в случае, если на вторичных нагрузках неравномерная нагрузка. После соединения в зигзаг нагрузка распределяется более равномерно по фазам и магнитный поток трансформатора сохраняет равновесие, несмотря на неравномерную нагрузку.

Рассмотрим соединение в зигзаг-звезду трехфазного силового трансформатора. Схематично изображение приведено на рисунке.

Первичные обмотки соединяются в звезду. Далее разделяем каждую вторичную обмотку напополам. И далее соединяем, как показано на рисунке.

При соединении в зигзаг-звезду потребуется большее число витков, чем при простой звезде. Также при таком соединении возможно получение трех классов напряжения, например 380-220-127В.

Сохраните в закладки или поделитесь с друзьями

Видео:Векторная диаграммаСкачать

§ 79. Соединение треугольником

Кроме соединения звездой, генераторы, трансформаторы, двигатели и другие потребители трехфазного тока могут включаться треугольником.

На рис. 179 представлена несвязанная трехфазная система. Объединяя попарно провода несвязанной шестипроводной системы и соединяя фазы так, как указано на чертеже, переходим к трехфазной трехпроводной системе, соединенной треугольником.

Рис. 179. Несвязанная трехфазная система

Как видно из рис. 180, соединение треугольником выполняется таким образом, чтобы конец фазы А был соединен с началом фазы В, конец фазы В соединен с началом фазы С и конец фазы С соединен с началом фазы A. К местам соединения фаз присоединяют линейные провода.

Рис. 180. Связанная трехфазная система, соединенная треугольником

Если обмотки генератора соединены треугольником, то, как видно на рис. 180, линейное напряжение создает каждая фазная обмотка. У потребителя, соединенного треугольником, линейное напряжение подключается к зажимам фазного сопротивления. Следовательно, при соединении треугольником фазное напряжение равно линейному:

Определим зависимость между фазными и линейными токами при соединении треугольником, если нагрузка фаз будет одинакова по величине и характеру. Составляем уравнения токов по первому закону Кирхгофа для трех узловых точек A 1 , В 1 и С 1 потребителя:

Отсюда видно, что линейные токи равны геометрической разности фазных токов. При симметричной нагрузке фазные токи одинаковы по величине и сдвинуты один относительно другого на 120°. Производя вычитание векторов фазных токов согласно полученным уравнениям, получаем линейные токи (рис. 181). Зависимость между фазными и линейными токами при соединении в треугольник показана на рис. 182:

Рис. 181. Фазные и линейные токи при соединении треугольником

Рис. 182. Зависимость между фазными и линейными токами при соединении треугольником

Следовательно, при симметричной нагрузке, соединенной треугольником, линейный ток в √3 раз больше фазного тока.

На рис. 183 дана векторная диаграмма токов и напряжений при равномерной активно-индуктивной нагрузке, соединенной треугольником. Построение диаграммы производится следующим образом. В выбранном масштабе строим равносторонний треугольник линейных напряжений сети UAB, UBC И UAC, которые равны фазным напряжениям потребителя. В сторону отставания под углами φAB, φBC, φСА к линейным напряжениям UAB, U BC и UСА строим в масштабе векторы фазных токов IAB, IBC и ICA. Затем, как было указано раньше, определяем линейные токи IА, IB и IС.

Рис. 183. Векторная диаграмма токов и напряжений при равномерной нагрузке, соединенной треугольником

У двигателей и у других потребителей трехфазного тока в большинстве случаев наружу выводят все шесть концов трех обмоток, которые по желанию можно соединять либо звездой, либо треугольником. Обычно к трехфазной машине крепится доска из изоляционного материала (клеммная доска), на которую и выводят все шесть концов.

Видео:Последовательное соединение активного сопротивления, индуктивности и емкостиСкачать

Определение

Нагрузка электрической цепи определяет, какой ток через неё проходит. Если ток постоянный, то эквивалентом нагрузки в большинстве случаев можно определить резистор определённого сопротивления. Тогда мощность рассчитывают по одной из формул:

По этой же формуле определяется полная мощность в цепи переменного тока.

Нагрузку разделяют на два основных типа:

• Активную – это резистивная нагрузка, типа – ТЭНов, ламп накаливания и подобного.
• Реактивную – она бывает индуктивной (двигатели, катушки пускателей, соленоиды) и емкостной (конденсаторные установки и прочее).

Последняя бывает только при переменном токе, например, в цепи синусоидального тока, именно такой есть у вас в розетках. В чем разница между активной и реактивной энергией мы расскажем далее простым языком, чтобы информация стала понятной для начинающих электриков.

Видео:Зачем нужны векторные диаграммы?Скачать

Схемы соединений обмоток треугольник и звезда для чайников.

Наиболее распространенный вопрос у начинающих изучения устройства трансформаторов или иных электротехнических устройств это «Что такое звезда и треугольник?». Чем же они отличаются и как устроены, попробуем разъяснить в нашей статье.

Рассмотрим схемы соединений обмоток на примере трехфазного трансформатора. В своем строении он имеет магнитопровод, состоящий из трёх стержней. На каждом стержне есть две обмотки – первичная и вторичная. На первичную подается высокое напряжения, а со вторичной снимается низкое напряжение и идет к потребителю. В условном обозначении схема соединений обозначается дробью (например, Y⁄∆ или Y/D или У/Д), значение числителя – соединение обмотки высшего напряжения (ВН), а значение знаменателя – низшего напряжения (НН).

Каждый стержень имеет как первичную обмотку так и вторичную (три первичных и три вторичных обмотки). У каждой обмотки есть начало и конец. Обмотки можно соединить между собой способом звезда или треугольник. Для наглядности обозначим вышеперечисленное схематически (рис. 1)

При соединении звездой, концы обмоток соединяются вместе, а из начал идут три фазы к потребителю. Из вывода соединений концов обмоток, выводят нейтральный провод N (он же нулевой). В итоге получается четырёх – проводная, трёхфазная система, которая часто встречается вдоль линий воздушных электропередач.(рис. 2)

Преимущества такой схемы соединения в том, что мы можем получить 2 вида напряжения: фазное (фаза+нейтраль) и линейное. В таком соединении линейное напряжение больше фазного в √3 раз. Зная, что фазное напряжение дает нам 220В, то умножив его на √3 = 1,73, получим примерно 380В – напряжение линейное. Но что касается электрического тока, то в этом случае фазный ток равен линейному, т.к. что линейный, что фазный токи одинаково выходят из обмотки, и другого пути у него нет. Так же стоит отметить что только в соединении звезда имеется нейтральный провод, который является «уравнителем» нагрузки, чтобы напряжение не менялось и не скакало.

Рассмотрим теперь соединение обмоток треугольником. Если мы конец фазы А, соединим с началом фазы В, конец фазы В соединим с началом фазы С, а конец фазы С соединим с началом фазы А, то получим схему соединения обмотки треугольником. Т.е. в этой схеме обмотки соединены последовательно. (рис. 3)

В основном такая схема соединения применяется для симметричной нагрузки, где по фазам нагрузка не изменяется. В таком соединении фазное напряжение равно линейному, а вот электрический ток, наоборот, в такой схеме разный. Ток линейный больше фазного тока в √3 раз. Соединение обмотки треугольником обеспечивает баланс ампер-виток для тока нулевой

последовательности. Простыми словами, схема соединения треугольником обеспечивает сбалансированное напряжение.

Подведем итоги. Для базового определения схем соединения обмоток силовых трансформаторов, необходимо понимать, что разница между этими соединениями состоит в том, что в звезде все три обмотки соединены вместе одним концом каждой из обмоток в одной (нейтральной) точке, а в треугольнике обмотки соединены последовательно. Соединение звезда позволяет нам создавать два вида напряжения: линейное (380В) и фазное (220В), а в треугольнике только 380В.

Выбор схемы соединения обмоток зависит от ряда причин:

• Схемы питания трансформатора
• Мощности трансформатора
• Уровня напряжения
• Асимметрии нагрузки
• Экономических соображений

Так например, для сетей с напряжением 35 кВ и более выгодно соединить обмотку трансформатора схемой звезда, заземлив нулевую точку. В данном случае получится, что напряжение выводов трансформатора и проводов линии передачи относительно земли будет всегда в √3 раз меньше линейного, что приведёт к снижению стоимости изоляции.

На практике чаще всего встречаются следующие группы соединений: Y/Y, D/Y, Y/D.

Группа соединений обмоток Y/Y (звезда/звезда) чаще всего применяется в трансформаторах небольшой мощности, питающих симметричные трёхфазные электроприборы/электроприемники. Так же иногда применяется в схемах большой мощности, когда требуется заземление нейтральной точки.

Группа соединения обмоток D/Y (треугольник/звезда) применяется, в основном в понижающих трансформаторах больших мощностей. Чаще всего трансформаторы с таким соединением работают в составе систем питания токораспределительных сетей низкого напряжения. Как правило, нейтральная точка звезды заземляется, для использования как линейного, так и фазного напряжений.

Группа соединений обмоток Y/D (звезда/треугольник) используется, в основном, в главных трансформаторах больших силовых станций и подстанций, не служащих для распределения.

Видео:Векторная диаграмма токов на комплексной плоскости вручнуюСкачать

Электрические цепи синусоидального тока

Содержание:

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Электрические цепи синусоидального тока:

В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.

При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.

Видео:Анализ не стандартной векторной диаграммы. часть 1Скачать

Цепь с активным сопротивлением

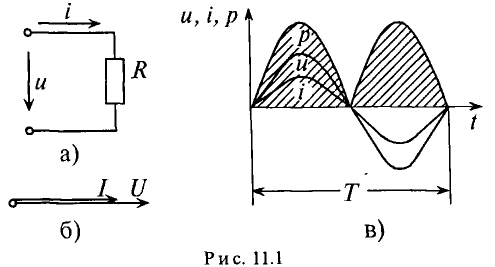
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).

Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение

где

Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны ( 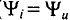= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.

Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 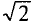=1,41.

Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.

Активная мощность

Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.

Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.

Количественно мощность в цепи с активным сопротивлением определяется следующим образом:

Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 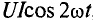, изменяющейся с двойной частотой.

Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть

Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:

где U- действующее значение напряжения; I— действующее значение тока.

Единицей активной мощности является ватт:

Поверхностный эффект и эффект близости

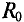
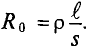
Сопротивление проводника постоянному току называют омическим сопротивлением и определяют выражением (2.8) Сопротивление проводника переменному току R называют активным.

Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е.

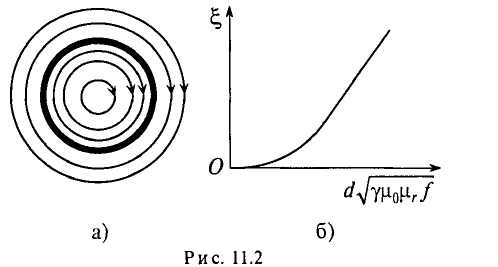
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).

На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.

Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.

Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 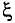(кси)

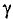
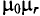
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости , магнитной проницаемости материала проводника и частоты переменного тока , проходящего по проводнику, показан на рис. 11.26.

При токах большой частоты (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.

На величину активного сопротивления проводника R оказывает влияние и эффект близости.

Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.

Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).

Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.

Видео:Лекция по электротехнике 4.1 - Двухполюсник. Треугольники сопротивлений и проводимостейСкачать

Цепь с идеальной индуктивностью

Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.

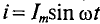
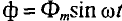
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток , то этот ток создает в катушке синусоидальный магнитный поток , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)

так как

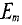
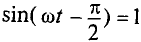
Очевидно, эта ЭДС достигает своего амплитудного значения тогда, когда :

Тогда

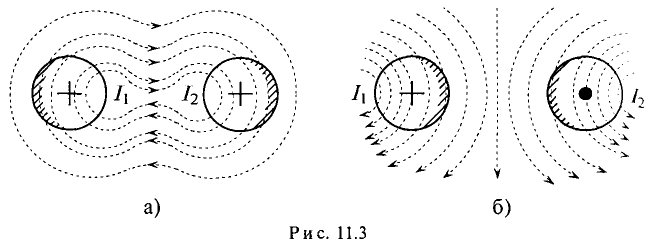
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 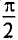(рис. 11.46, в).

По второму закону Кирхгофа для мгновенных значений можно записать

Откуда

Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):

Очевидно, напряжение достигает своего амплитудного значения U_m тогда, когда :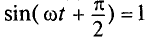

Следовательно,

Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 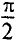(рис. 11.46, в).

Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).

Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 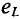противодействует изменению тока.

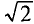
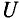
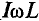
Если уравнение (11.10) разделить на =1,41, то получается =, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением X_L.

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление X_L — это противодействие, которое ЭДС самоиндукции e_L оказывает изменению тока.

Реактивная мощность в цепи с индуктивностью

Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока

где

Следовательно,

Полученное уравнение умножают и делят на 2:

Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.

Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.

Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (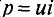) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.

То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно

Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.

Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.

Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.

Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).

Величина реактивной мощности в рассматриваемой цепи определяется выражением

Так как реактивная мощность Q_L имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. X_L.

Видео:ТОЭ│Задача на переменный ток. Определить сопротивления элементов. Векторная диаграммаСкачать

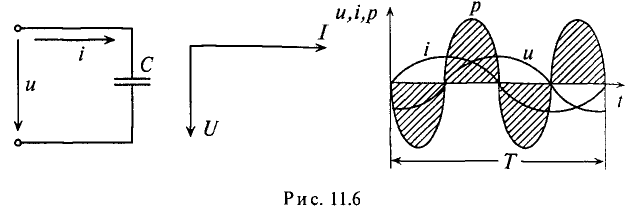
Цепь с емкостью

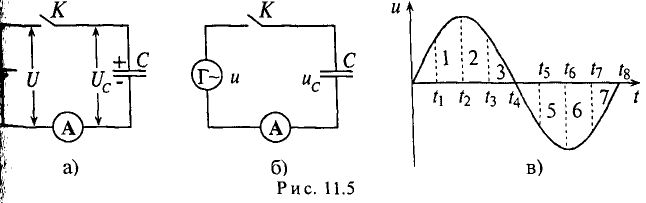
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе U_c не станет равным напряжению источника U.

Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).

Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе U_c отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 — конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 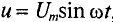, то в цепи конденсатора проходит ток i (рис. 11.6а):

где q= Си согласно (6.3).

Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда :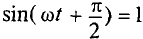

Тогда

Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=

Следовательно, напряжение отстает по фазе от тока на 90° = (рис. 11.66).

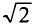
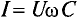
Если уравнение (11.17) разделить на = 1,41, то получится равенство или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.

Очевидно, знаменатель этого равенства является сопротивлением конденсатора Х_с, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).

Реактивная мощность в цепи с конденсатором

Если в цепи конденсатора емкостью 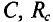= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:

Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно

Мгновенная мощность в цепи с конденсатором

Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).

Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.

Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.

Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно

В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.

Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.

Величина реактивной мощности в цепи конденсатора определяется выражением

Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) — аналитическом выражении мгновенной мощности в цепи с конденсатором.

Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Х_с).

Видео:Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

Расчет линейных электрических цепей синусоидального тока

Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.

Цепь с активным сопротивлением и индуктивностью

Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 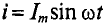(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки

Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

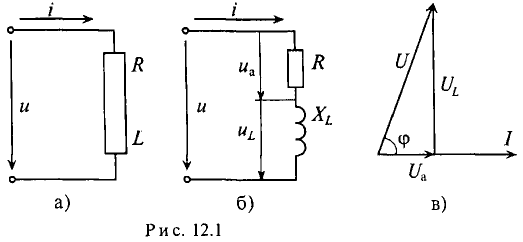
Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением X_L (рис. 12.16).

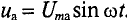
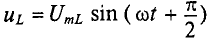
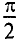
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано . Индуктивное напряжение опережает ток на угол 90° = .

Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 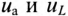согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений

Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).

Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 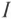на угол ф. Мгновенное значение этого напряжения может быть записано:

где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.

Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.

Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Z_k — полное, или кажущееся, сопротивление реальной катушки.

Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.

Треугольники напряжений, сопротивлений, мощностей

Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).

Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:

Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:

Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).

Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).

Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е.

Однако потребляется в цепи только часть полной мощности — активная мощность

где cos ф показывает, какая часть полной мощности 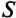потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:

Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.

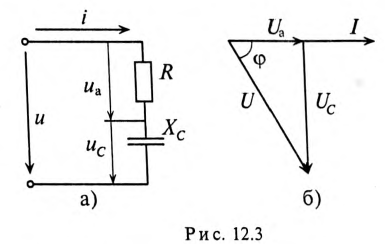
Цепь с активным сопротивлением и емкостью

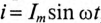
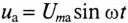
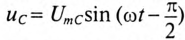
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток , то он создает падение напряжения на активном сопротивлении и на емкостном сопротивлении . Векторная диаграмма для этой цепи изображена на рис. 12.36.

Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📹 Видео

Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать