В треугольнике вписана окружность вычислите углы треугольника

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Треугольник LMN, вписанный в окружность, делит ее на три дуги?

Геометрия | 5 — 9 классы

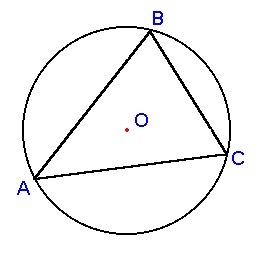
Треугольник LMN, вписанный в окружность, делит ее на три дуги.

Вычисли угол LON и углы треугольника LMN, если даны два центральных угла : ∢LOM = 140° и ∢MON = 170°.

Ребята очень прошу помогите.

Только на рисунке обозначение не АВС , а MNL.

∠LOM = 360 — 170 — 140 = 50

∠L = (180 — 50) / 2 + (180 — 140) / 2 = 65 + 20 = 85

∠M = (180 — 140) / 2 + (180 — 170) / 2 = 20 + 5 = 25

∠N = (180 — 170) / 2 + (180 — 50) / 2 = 65 + 5 = 70.

Видео:№703. В окружность вписан равнобедренный треугольник ABC с основанием ВС. Найдите углы треугольникаСкачать

Равнобедренный треугольник ABC с основанием АС вписан в окружность с ценьром О найти углы треугольника АВС если угол АОС = 118?

Равнобедренный треугольник ABC с основанием АС вписан в окружность с ценьром О найти углы треугольника АВС если угол АОС = 118.

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Какие из следующих утверждений равны?

Какие из следующих утверждений равны?

1) В любой ромб можно вписать окружность.

2) Все высоты равностороннего треугольника равны.

3) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Вписанная в треугольник ABC окружность касается его сторон в точках L M и N доказать что треугольник LMN остроугольный?

Вписанная в треугольник ABC окружность касается его сторон в точках L M и N доказать что треугольник LMN остроугольный.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Центральный угол АОВ на 50° больше угла, вписанного в окружность и опирающегося на дугу АВ?

Центральный угол АОВ на 50° больше угла, вписанного в окружность и опирающегося на дугу АВ.

Найдите каждый из этих углов.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Точки А, В и С делят окружность на три дуги так, что дуга АВ относится к дуге ВС и относится дуга АС = 3 : 5 : 7?

Точки А, В и С делят окружность на три дуги так, что дуга АВ относится к дуге ВС и относится дуга АС = 3 : 5 : 7.

Найдите углы треугольника АВС.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

В треугольнике авс угол : углу в : углу с = 5 : 6 : 7?

В треугольнике авс угол : углу в : углу с = 5 : 6 : 7.

Найдите углы треугольника авс.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Центральный угол на 62 градусов больше острого вписанного угла, опирающегося на ту же дугу окружности?

Центральный угол на 62 градусов больше острого вписанного угла, опирающегося на ту же дугу окружности.

Найдите вписанный угол.

Ответ дайте в градусах.

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

1. Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80, дуга ВС : дуга АВ = 3 : 2?

1. Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80, дуга ВС : дуга АВ = 3 : 2.

Найти углы треугольника ОАВ.

Видео:Внешний угол треугольникаСкачать

Треугольник LMN, вписанный в окружность, делит её на три дуги?

Треугольник LMN, вписанный в окружность, делит её на три дуги.

Вычисли угол LON и углы треугольникаLMN, если даны два центральных угла : ∢MOL = 140° и ∢NOM = 120°.

Видео:Треугольник, вписанный в окружность геометрия 7 классСкачать

В прямоугольный треугольник ABC вписана окружность, угол B — прямой?

В прямоугольный треугольник ABC вписана окружность, угол B — прямой.

Вычисли углы треугольника A и C, а также центральные углы, если ∢EOF = 102°.

Ребята очень прошу помогите.

На этой странице сайта вы найдете ответы на вопрос Треугольник LMN, вписанный в окружность, делит ее на три дуги?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Ответ : 720 Треугольник со сторонами 26, 26, 20 (основание и по 2 / 3 медиан) имеет площадь 240 и равен 1 / 3 площади искомого.

А ты знала что есть такое понятие ВВ ПОМОЩЬ? 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 5 Крч намёк ты поняла Помощь И = 1 + 0 + 9 + 2 + 3 + 8 + 4 + 7 + 5 + 6.

Треугольники DOA и BOC подобны. Из подобия следует : BC : AD = AO : OC Обозначим AO = x, тогда OC = 20 — x 3 : 7 = x : (20 — x) 3 * (20 — x) = 7x 60 — 3x = 7x 10x = 60 x = 6 то есть AO = 6.

Да, равны. По двум сторонам и углу между ними.

В квадрате = АА1 в квадр + А1В в квадрате А1В в квад = 6 в квад + 7 в ква = 36 + 49 = 85 АВ в квад = 25 + 85 = 110 ответ корнь из110 .

48 + 42 + 90(прямой угол) = 180 градусов, да ровны.

D = √ ( (x2 — x1) ^ 2 + (y2 — y1) ^ 2) d = √ ( (1 — 4) ^ 2 + (2 + 2 ) ^ 2) = √ ( 3 ^ 2 + 4 ^ 2) = √ (9 + 16) = √ 25 = 5.

Проекцией прямой МД на плоскость ромба является его диагональ ВД, а так как диагонали ромба перпендикулярны то АС⊥МД.

3. Объем призмы по формуле V = S * h Вычисляем площадь основания — S. Находим второй катет — по т. Пифагора. С = 17 см — гипотенуза а = 8 см — катет Второй катет b² = 17² — 8² = 289 — 64 = 225 b = √225 = 15 см — . Площадь основания S = a * b / 2 ..

Т. к. АВ 17 см, то АК = 17 : 2 = 8, 5 см и КВ = 17 : 2 = 8, 5 см т. К. а — середина, то МК = 8, 5 * 2 = 17 сми КР = 17 см МР = 17 + 17 = 34 см ну как то так. Желаю удачи.

Видео:Вписанные углы в окружностиСкачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:8 класс, 38 урок, Вписанная окружностьСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

🔍 Видео

Радиус описанной окружностиСкачать