В трапецию abcd вписана окружность касающаяся боковой стороны ab

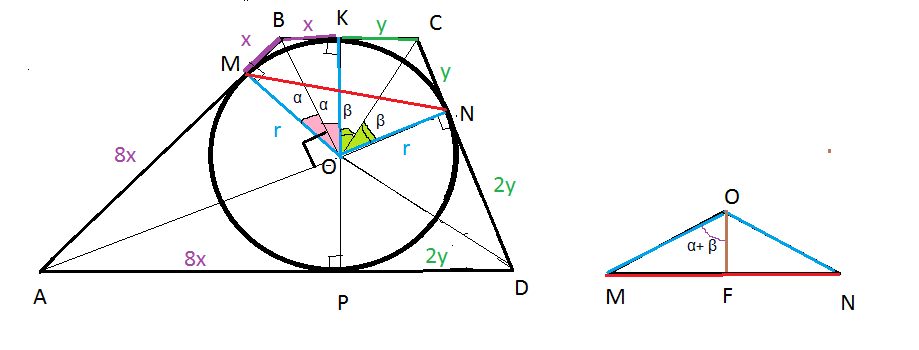
Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN.

а) Докажите, что AD = 4BC.

б) Найдите длину отрезка MN, если радиус окружности равен

а) Пусть окружность касается оснований BC и AD в точках K и L соответственно, а ее центр находится в точке O.

Лучи AO и BO являются биссектрисами углов BAD и ABC соответственно, поэтому

то есть треугольник AOB прямоугольный. Аналогично, треугольник COD тоже прямоугольный. Пусть BM = x, CN = y, тогда AM = 8x, DN = 2y.

б) Заметим, что поэтому

Пусть прямые AB и CD пересекаются в точке P, а прямые MN и PO пересекаются в точке Q. Тогда треугольники BPC и APD подобны, поэтому AP = 4BP, AB = 3BP, BP = 3x, PN = PM = 4x. Прямая PO является серединным перпендикуляром к MN. В прямоугольном треугольнике OMP получаем:

Значит,

Приведем другое решение пункта а)

Пусть окружность касается оснований BC и AD в точках K и L соответственно, ее центр находится в точке O, а BM = x, CN = y, тогда AM = 8x, DN = 2y. Поскольку точки M, K, N и L — точки касания, и Опустим высоты BH и CQ:

тогда по теореме Пифагора Поскольку имеем откуда

Видео:Математика 11, задача по геометрии, 2-я часть ЕГЭ, задача 16Скачать

Задача 16865 Окружность, вписанная в трапецию ABCD.

Условие

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон АВ и CD в точках М и N соответственно. Известно, что АМ=8МВ и DN=2CN.

а) Докажите, что AD=4BC.

б) Найдите длину отрезка MN, если радиус окружности равен sqrt(6)

Решение

а)
Пусть ВМ=х, тогда АМ=8х
СN=y, тогда DN=2y
По свойству касательной, проведенной к окружности из одной точки, отрезки касательных равны.
Поэтому
ВМ=ВК=x
СN=CK=y
AM=AP=8x
DN=DP=2y

Сумма углов трапеции, прилежащих к боковой стороне, равна 180 градусов.
Биссектрисы АО и ВО делят углы А и В пополам, значит сумма острых углов треугольника АОВ равна 90 градусов.
Треугольник АОВ- прямоугольный.
Высота ОM прямоугольного треугольника АОВ есть среднее пропорциональное между отрезками АМ и ВМ.
ОM^2=AM*BM
OM=r
r^2=8x*x
r^2=8x^2
Аналогично, Δ СOD — прямоугольный и
ON^2=CN*ND
r^2=y*2y
r^2=2y^2

AD=AP+DP=8x+2y=8x+2*2x=12x
BC=BK+CK=x+y=x+2x=3x/(sqrt(x^2+r^2
AD=12x=4*(3x)=4BC

б)
r=sqrt(6)
Обозначим
∠ МОВ= ∠ ВОК= альфа
∠ KOC= ∠ CON= бета
sin альфа =MB/BO=x/sqrt(x^2+r^2)
cos альфа =MO/BO=r/sqrt(x^2+r^2)
sin бета=CN/CO=y/sqrt(y^2+r^2)
cos бета =ON/CO=r/sqrt(y^2+r^2)

sin( альфа + бета )=
=sin альфа*cos бета +cos альфа *sin бета =
=r*(x+y)/(sqrt(x^2+r^2)*sqrt(y^2+r^2))

Треугольник MON — равнобедренный,
МО=ОN=r
∠ MON=2*( альфа + бета )
Высота ОF делит основание MN пополам и сторону MN пополам.
MF=(1/2)MN=OM*sin( альфа + бета )=
MN=2*r*r*(x+y)//(sqrt(x^2+r^2)*sqrt(y^2+r^2))
Так как у=2х и r^2=6 и r^2=8x^2; r^2=2y^2, то
MN=
=2*r^2*((r/sqrt(8))+(r/sqrt(2)))/(r*sqrt((1/8)+1)*r*sqrt((1/2)+1))=
=(2*r*3/(2sqrt(2)))/(sqrt(9/8)*sqrt(3/2))=4

О т в е т. MN=4

Видео:Задача про трапецию, описанную около окружностиСкачать

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно?

Геометрия | 5 — 9 классы

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно.

Известно, что AM = 8MB и DN = 2CN.

Докажите, что AD = 4BC.

А) Пусть окружность касается основанийBCиADв точкахKиLсоответственно, а ее центр находится в точкеO.

ЛучиAOиBOявляются биссектрисами угловBADиABCсоответственно, поэтому.

Так как касательные к окружности из одной точки равны, то :

BC + AD = 9MB + 3CN.

AD = 6MB + 3BC — BC или

AD = 8MB + 2CN = 6MB + 2BC.

Треугольники АВО и СОD — прямоугольные (так как боковая сторона трапеции видна из центра вписанной в нее окружности под углом 90° — свойство).

Высоты ОМ и ОN (равные радиусу) равны.

По свойству высоты из прямого угла имеем :

ОМ = (2√2) * МВ ; ОN = √2 * CN.

Тогда 6МВ = 2МВ + 4МВ = 2МВ + 2CN = 2ВС.

AD = 6MB + 2BC (доказано выше).

AD = 2BC + 2BC = = 4ВС, что и требовалось доказать.

Видео:В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. окружность проходит через точки C,DСкачать

В трапецию вписана окружность?

В трапецию вписана окружность.

Найти периметр трапеции если ее боковые стороны равны 7см и 9см.

Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Точка E середина боковой стороны CDMA трапеции ABCD?

Точка E середина боковой стороны CDMA трапеции ABCD.

Докажите что площадь треугольника ABE равна половине площади трапеции.

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

45 баллов?

Основания AD и BC трапеции ABCD и боковая сторона AB равны соответственно 21, 7 и 12.

Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если сумма углов при основании трапеции равна 90 градусов.

Видео:Геометрия В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причёмСкачать

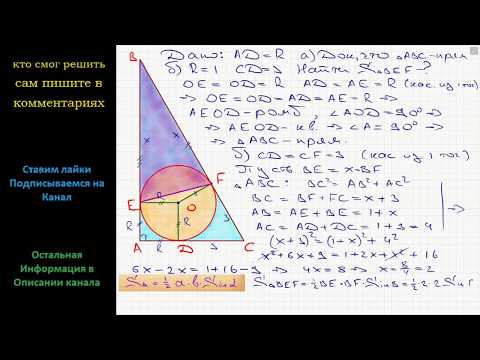
В трапеции АВСД углы при вершинах А и В прямые, а боковая сторона СД ровно вдвое длинее меньшего основания ВС?

В трапеции АВСД углы при вершинах А и В прямые, а боковая сторона СД ровно вдвое длинее меньшего основания ВС.

Известно, что в эту трапецию можно вписать окружность.

Построена окружность, которая касается большего основания АД, боковой стороны СД и вписанной окружности трапеции.

А) Прямая, проходящая через центр построенной окружности и центр окружности, вписанной в трапецию, пересекает сторону АВ в точке Р.

Докажите, что АР / ВР = АД / ВС.

Б) Найти радиус плстроенной окружности, если радиус вписанрой в трапецию окружности равен 1.

Видео:Окружность, вписанная в трапециюСкачать

Боковая сторона равнобедренного треугольника равна 18, основание равно 12?

Боковая сторона равнобедренного треугольника равна 18, основание равно 12.

Вписанная окружность касается боковых сторон в точках С и Е.

Видео:Геометрия В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит черезСкачать

Боковая сторона равнобедренного треугольника равна 18, основание равно 12?

Боковая сторона равнобедренного треугольника равна 18, основание равно 12.

Вписанная окружность касается боковых сторон в точках С и Е.

Видео:Планиметрия 3 | mathus.ru | трапеция и окружностьСкачать

В трапеции ABCD основания AD и BC равны соответственно 5 и 2?

В трапеции ABCD основания AD и BC равны соответственно 5 и 2.

Окружность, описанная около треугольника ABC, касается основания AD и боковой стороны CD.

Найти радиус окружности.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Большая боковая сторона прямоугольной трапеции равна 12корень из 2см, а острый угол — 45°?

Большая боковая сторона прямоугольной трапеции равна 12корень из 2см, а острый угол — 45°.

Найдите площадь трапеции, если известно, что в нее можно вписать окружность.

Видео:ЕГЭ Задание 16 Трапеция и две окружностиСкачать

Большая боковая сторона прямоугольной трапеции равна 12√2см, а острый угол — 45°?

Большая боковая сторона прямоугольной трапеции равна 12√2см, а острый угол — 45°.

Найдите площадь трапеции, если известно, что в нее можно ВПИСАТЬ окружность.

Видео:Планиметрия с окружностями | Задачи из ЕГЭ прошлых лет | №17 ЕГЭ по математикеСкачать

В трапецию абсд вписана окружность с центром и?

В трапецию абсд вписана окружность с центром и.

Найдите периметр трапеции если сумма растояний от точки и до середин боковых сторон равна 30.

Видео:🔴 ВСЕ ЗАДАНИЯ 26 ИЗ ОТКРЫТОГО БАНКА (ВТОРАЯ ПОЛОВИНА ВСЕХ ЗАДАЧ) | ОГЭ 2017Скачать

В трапецию вписана окружность, точка касания окружности с боковой стороной делит эту сторону на два отрезка — 8 и 2?

В трапецию вписана окружность, точка касания окружности с боковой стороной делит эту сторону на два отрезка — 8 и 2.

Найти высоту трапеции.

Вы зашли на страницу вопроса Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

1. задание : найти АС. Что это значит? ЭТО значит, что 6 см + 9 см = 15 см , так как АВ = 6 см , а ВС = 9 см, задание НАЙТИ АС. 2. ЗАДАНИЕ : найти МК всё точно также складываем 12см + 3 см = 15 см 3. Найти ошибку там ты написала правильно что 6, ..

Дано : AM = MN = NB и МК||NP||BC. Проведем МЕ и ND параллельно АС. Теорема ФалесаЕсли на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второ..

24 — 8 = 16см — это ВС АС = 8см.

Возможно, кому — то пригодится решение — привожу своё : Пусть BC = AD = aBC = AD = a, тогда из условия BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5. MOMO и ONON найдём как средние линии трапеций ..

Решение 22см — одна из сторон, т. К. сумма от точки пересекч к соседним сторонам равна одной стороне. 22 — 6 = 16см — вторая сторона.

Х + х — 6 = 22 2х — 6 = 22 2х = 22 + 6 2х = 28 х = 28 / 2 х = 14 одна сторона это Х то есть 14 а вторая х — 6 то есть 14 — 6 = 8.

1) вектор а = 2i — j 2) координаты вектора c .

Вот, пожалуйста✩ ^ _ ^ Все очень просто решается по теореме Пифагора.

Решение задания приложено.

ВС = MB — MC = 18, 2 — 9, 4 = 8, 8 Ответ : 1.

🌟 Видео

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Трапеция и окружность. 9 классСкачать

Планиметрия. №9. (16 задача ЕГЭ).Скачать

Геометрия Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CDСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

✓ Как решить трапецию | ЕГЭ-2020. Задание 16. Профильный уровень. Основная волна | Борис ТрушинСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать