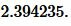Вопрос по геометрии:
В равнобедренный треугольник вписана окружность радиуса корень из 3.Угол при основании 60 градусов.Найти основание.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- Как написать хороший ответ?
- В равнобедренный треугольник вписана окружность радиуса корень из 3?
- Основание равнобедренного треугольника равно16см, боковая сторона17см?
- В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности?
- Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности?
- Срочно) Основание равнобедренного треугольника равно 12?
- Площадь равнобедренной трапеции 72см кв?
- В равнобедренный треугольник с основанием 12см и периметром 32см вписана окружность?
- В равнобедренный треугольник вписана окружность радиусом корень из 3 — ех, угол при основании равен 60 градусов?
- Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
- Угол при основании равнобедренного треугольника равен a?
- В равнобедренном треугольнике угол при основании равен 32 градусам найти угол при основании?
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- 1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- 2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- 3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- 4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- 5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
- 💥 Видео
Ответы и объяснения 2
Если угол при основании равен 60, то противоположный угол будет равен тоже 60, следовательно и угол при вершине равен 60. получается равно стороний треугольник. По формуле радиуса в равновносторонем треугольнике найдём его сторону. , где а — сторона треугольника.
так как это равностороний треугольник, то все стороны будут равны 6 и основание тоже.
извините за кривую окружность)
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

В равнобедренный треугольник вписана окружность радиуса корень из 3?
Геометрия | 5 — 9 классы
В равнобедренный треугольник вписана окружность радиуса корень из 3.
Угол при основании 60 градусов.
Если угол при основании равен 60, то противоположный угол будет равен тоже 60, следовательно и угол при вершине равен 60.
Получается равно стороний треугольник.
По формуле радиуса в равновносторонем треугольнике найдём его сторону.
так как это равностороний треугольник, то все стороны будут равны 6 и основание тоже.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Основание равнобедренного треугольника равно16см, боковая сторона17см?
Основание равнобедренного треугольника равно16см, боковая сторона17см.
Найти радиус вписанной и описанной окружности.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности?
В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности.
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности?
Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности.
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Срочно) Основание равнобедренного треугольника равно 12?
Срочно) Основание равнобедренного треугольника равно 12.
Радиус вписанной окружности равен 3.
Найти площадь треугольника!
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Площадь равнобедренной трапеции 72см кв?
Площадь равнобедренной трапеции 72см кв.
Угол при основании 30 град.
Найти радиус вписанной окружности.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В равнобедренный треугольник с основанием 12см и периметром 32см вписана окружность?
В равнобедренный треугольник с основанием 12см и периметром 32см вписана окружность.
Найдите радиус этой окружности.
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

В равнобедренный треугольник вписана окружность радиусом корень из 3 — ех, угол при основании равен 60 градусов?
В равнобедренный треугольник вписана окружность радиусом корень из 3 — ех, угол при основании равен 60 градусов.
Надо найти основание треугольника.
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.
Найти радиус вписанной и радиус описанной окружности.
Видео:ЕГЭ Математика Задание 6#27935Скачать

Угол при основании равнобедренного треугольника равен a?
Угол при основании равнобедренного треугольника равен a.
Радиус вписанной окружности равен r.
Найти стороны треугольника и радиус описанной окружности.
Видео:2071 радиус окружности вписанной в правильный треугольник равен корень из 3 на 2Скачать

В равнобедренном треугольнике угол при основании равен 32 градусам найти угол при основании?
В равнобедренном треугольнике угол при основании равен 32 градусам найти угол при основании.
Вы перешли к вопросу В равнобедренный треугольник вписана окружность радиуса корень из 3?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Пусть в треугольнике ABC известны стороны AB = c, BC = b и медиана BM = m. На луче AM отложим отрезок MD, MD = AM и соединим точку D с точками B и C. Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD..
∠АВС = ∠А₁АС + ∠С₁СА ∠А₁АС = ∠С₁СА = х х + х + 130 = 180 2х + 130 = 180 2х = 180 — 130 2х = 50 х = 25 = ∠А₁АС = ∠С₁СА Тогда : ∠АВС = 25 + 25 = 50 Пусть ∠А = ∠С = у Тогда : у + у + 50 = 180 2у + 50 = 180 2у = 130 у = 65 = ∠А = ∠С ∠АА₁В = 180 — (ВАА₁ +..
Весь циферблат равен 360°. Каждые 5 минут — это 30° (360 : 12 = 30). 5 час — это отсек 25 минуты. Так же известно, что есть 10 минут. Получается, что угол занимает по три пятиминутки ((25 — 10) : 5 = 3) Узнаём градусную меру : 3•30° = 90°.
Большая дуга относится к меньшей как 4 : 1. Т. е. Большая дуга — 4 части, меньшая — 1 часть. Вся окружность — 5 частей. Градусная мера окружности 360°, откуда 1 часть = 360° : 5 = 72°. Это меньшая дуга. Большая дуга = 72 * 4 = 288°. Ответ : 72..
По теореме Пифагора : смНайдем синус угла B : sinB = AC / AB = 5 / 10 = 1 / 2значит, В = 30 градусов.
ABCD — трапеция (буквы можешь расположить, как хочешь)AC — диагональBC = 10L ACB = L DL CAD = L ACB (по свойству трапеции) — — — — — — > L D = L CAD — — — — — > AC = CDL ACB = L CAD — — — — — > L BAD = 90 град. — — — — > L D = L CAD = L ACB = 90 2..
M(x1 ; y1) n(x2 ; y2) середина = ((x2 — x1) / 2 ; (y2 — y1) / 2) 1) (5 ; 2) 2)(1 ; 3) 3)(1, 5 ; 4, 5).
S = 6 * 10 * 8 * 20 = 9600 Вот.
Всё 12 ребер у куба равны. Найдем длину одного : 48 : 12 = 4 Все 6 граней — равные квадраты. Тогда площадь S = 6 * 4² = 6 * 16 = 96.
Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
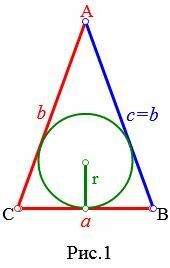 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
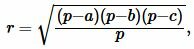 | (1) |
где полупериметр p вычисляется из формулы:
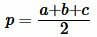 . . | (2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac ) ( small =frac, ) | (3) |
| ( small p-a=frac-a ) ( small =frac, ) | (4) |
| ( small p-b=p-c=frac-b ) ( small =frac. ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
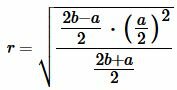 , , |
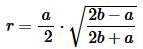 . . | (6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
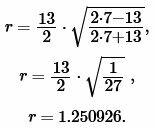 |
Ответ:
Видео:Задание 26 ОГЭ по математике. Равнобедренный треугольник вписан в окружность, радиус которой равенСкачать

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
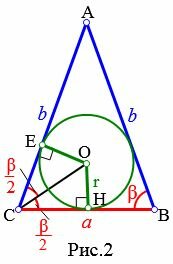 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac. ) Для прямоугольного треугольника OCH можно записать:
| ( small frac=frac<large frac>=mathrmfrac .) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac cdot mathrmfrac .) | (8) |
| ( small r=frac cdot frac .) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
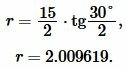 |
Ответ:
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
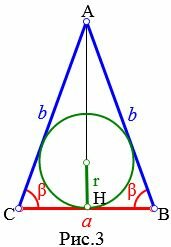 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| ( small frac=frac<large frac>= cos beta .) |
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=frac cdot mathrmfrac=frac cdot mathrmfrac ) ( small =b cos beta cdot mathrmfrac ) |
| ( small r=b cdot cos beta cdot mathrmfrac ) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac ) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
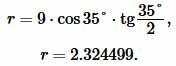 |
Ответ:
Видео:2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
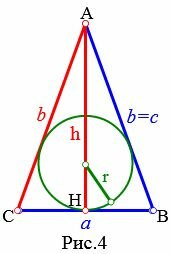 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
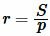 , , | (13) |
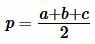 | (14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| ( small left( fracright)^2=b^2-h^2 ) |
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac ) ( small =frac ) ( small =frac+b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac ) ( small =frac<large h cdot sqrt><large b+ sqrt> ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
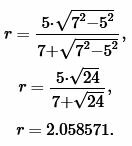 |
Ответ:
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать
5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
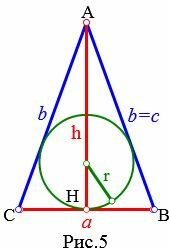 |
Из формулы (15) найдем b:
| ( small b^2-h^2=left( frac right)^2 ) |
| ( small b^2= frac +h^2 ) |
| ( small b= frac cdot sqrt) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=frac<large h cdot sqrt><large b+ sqrt>) ( small =frac<large h cdot sqrt<frac+h^2-h^2>><large frac cdot sqrt+ sqrt<frac+h^2-h^2>>) ( small = large frac< h cdot frac>< frac cdot sqrt+frac >) |
| ( small r=large frac<a+ sqrt>) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
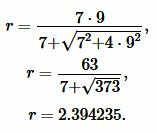 |
Ответ:
💥 Видео
Окружность вписана в равносторонний треугольник, найти радиусСкачать

Формулы для радиуса окружности #shortsСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать