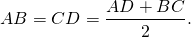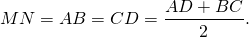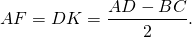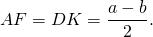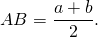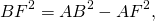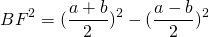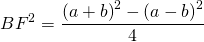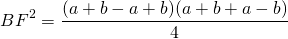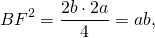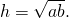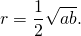В равнобедренную трапецию с боковой стороной 10 вписана окружность

Решение:
Самая распространенная формула для вычисления площади трапеции — S = (a+b)h/2. Для случая равнобедренной трапеции она явным образом не поменяется. Можно лишь отметить, что у равнобедренной трапеции углы при любом из оснований будут равны (DAB = CDA = x). Так как ее боковые стороны тоже равны (AB = CD = с), то и высоту h можно посчитать по формуле h = с*sin(x).
Тогда S = (a+b)*с*sin(x)/2.
Аналогично, площадь трапеции можно записать через среднюю сторону трапеции: S = mh. h = диаметру окружности, т. е 6 итак площадь = 6*10=60

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

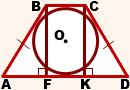
Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

Видео:Задача про трапецию, описанную около окружностиСкачать

В равнобедренную трапецию с боковой стороной с и площадью S вписана окружность радиуса r?

Геометрия | 5 — 9 классы

В равнобедренную трапецию с боковой стороной с и площадью S вписана окружность радиуса r.

Докажите, что S = 2cr.

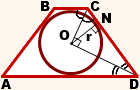
Равнобедренная трапеция : боковые стороны с, нижнее основание а и верхнее основание b, высота трапеции h.

В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон : 2с = а + b.

Такжевысота трапеции совпадает с диаметром вписанной окружности, значит h = 2r.

S = (a + b) * h / 2 = 2c * 2r / 2 = 2cr.

Видео:Задание 24 ОГЭ по математике #4Скачать

В равнобедренную трапецию площадью 28 вписана окружность радиуса 2?

В равнобедренную трапецию площадью 28 вписана окружность радиуса 2.

Найдите боковую сторону трапеции.

Видео:8 класс, 6 урок, ТрапецияСкачать

В равнобедренную трапецию вписана окружность?

В равнобедренную трапецию вписана окружность.

Точка касания окружности с боковой стороной делит эту сторону на отрезки с длинами 16 и 25.

Найти площадь трапеции.

Видео:№1034. В равнобедренной трапеции меньшее основание равно боковой стороне, большее основаниеСкачать

Дана равнобедренная трапеция, её площадь равна 125?

Дана равнобедренная трапеция, её площадь равна 125.

В трапецию вписана окружность так, что расстояние между точками касания её боковых сторон равно 8.

Найдите радиус окружности, вписанной в трапецию.

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Окружность радиуса 12 вписана в равнобедренную трапецию?

Окружность радиуса 12 вписана в равнобедренную трапецию.

Точка касания окружности с боковой стороной трапеции делит эту сторону в отношении 1 : 4.

Найдите периметр трапеции.

Видео:В равнобедренной трапеции большее основание равно 25 а боковая сторона равна 10 угол между ними 60°Скачать

Радиус вписанного в равнобедренную трапецию окружности равняется 12см?

Радиус вписанного в равнобедренную трапецию окружности равняется 12см.

Боковая сторона 25см.

Найти основания трапеции.

Видео:Геометрия В равнобедренную трапецию, меньшее основание которой равно 4 см, вписана окружностьСкачать

Окружность радиуса 12 вписана в равнобедренную трапецию?

Окружность радиуса 12 вписана в равнобедренную трапецию.

Точка касания окружности с боковой стороной трапеции делит эту сторону в отношении 1 : 4.

Найдите периметр трапеции.

Видео:Трапеция, вписанная в окружностьСкачать

В равнобедренную трапецию вписана окружность радиуса 2?

В равнобедренную трапецию вписана окружность радиуса 2.

Найдите площадь трапеции если длинна боковой стороны равна 10.

Видео:Задание 26_Равнобедренная трапеция. Вписанная окружность.Скачать

В равнобедренную трапецию с боковой стороной, равной 10 м, вписана окружность радиуса 3 м?

В равнобедренную трапецию с боковой стороной, равной 10 м, вписана окружность радиуса 3 м.

Найдите площадь трапеции.

Видео:В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать

В равнобедренную трапецию с основаниями 8 и 2 вписана окружность?

В равнобедренную трапецию с основаниями 8 и 2 вписана окружность.

Найдите радиус окружности касающейся большего основания боковой стороне и вписанной окружности.

Видео:Геометрия Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой сторонойСкачать

В равнобедренную трапецию ABCD с основаниями BC = 9см AD = 25см вписана окружность с центром О а) найдите длину боковой стороны трапеции б) найдите радиус вписанной окружности в) докажите что треуголь?

В равнобедренную трапецию ABCD с основаниями BC = 9см AD = 25см вписана окружность с центром О а) найдите длину боковой стороны трапеции б) найдите радиус вписанной окружности в) докажите что треугольник АОВ прямоугольный.

На этой странице находится ответ на вопрос В равнобедренную трапецию с боковой стороной с и площадью S вписана окружность радиуса r?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

💡 Видео

Определение сильных и слабых точек структуры.Скачать

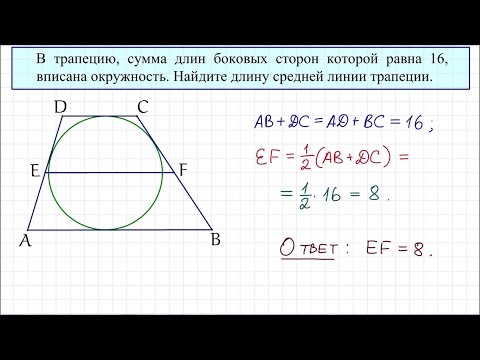
Геометрия В трапецию, сумма длин боковых сторон равна 16, вписана окружность. Найдите длину среднейСкачать

ЗАДАЧА ВЗОРВАЛА ИНТЕРНЕТ! НИКТО НЕ РЕШИЛ!Скачать

Лента Мёбиуса с Мэттом Паркером (фрагмент шоу "Четырехмерная математика")Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

ЕГЭ Математика Задание 6#27935Скачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

№527. В равнобедренной трапеции диагональ равна 10 см, а высота равна 6 см. Найдите площадь трапецииСкачать