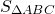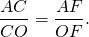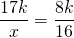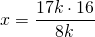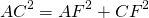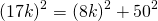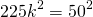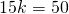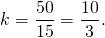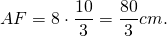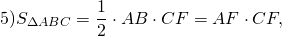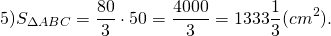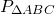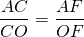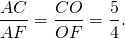В равнобедренном треугольнике центр вписанной окружности делит высоту проведенную

Видео:№690. Найдите основание равнобедренного треугольника, если центр вписанной в него окружностиСкачать

Ваш ответ

Видео:Геометрия Центр окружности, вписанной в равнобедренный треугольник, делит его высоту, проведеннуюСкачать

решение вопроса

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,044
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

Центр вписанной окружности делит высоту равнобедренного треугольника, опущенную на основание, на отрезки 5 см и 3 см, считая от вершины?

Геометрия | 10 — 11 классы

Центр вписанной окружности делит высоту равнобедренного треугольника, опущенную на основание, на отрезки 5 см и 3 см, считая от вершины.

Определите длину основания треугольника.

Пусть окружность вписана в треугольник АВС.

ВН — высота, биссектриса и медиана треугольника АВС.

ВН = ВО + ОН = 5_3 = 8 см

К — точка касания окружности и боковой стороны.

В прямоугольном треугольнике ВКО ВК = 4 ( треугольник — египетский, можно проверить по т.

Треугольники ВНС и ВКО — подобны( прямоугольные с общим острым углом при В).

АС = 2 * 6 = 12 см.

Видео:Центр описанной окружности равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Боковая сторона равнобедренного треугольника равна 10, а основание 16?

Боковая сторона равнобедренного треугольника равна 10, а основание 16.

На какие отрезки делятся высота треугольника, опущенной из вершины, биссектрисой угла при основании?

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см?

Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см.

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

В равнобедренный треугольник вписали окружность?

В равнобедренный треугольник вписали окружность.

Точка касания делит боковую сторону треугольника на отрезки длиной 12 см и 6 см , считая от основания.

Вычислите периметр треугольника.

Видео:Геометрия Радиус окружности вписанной в равнобедренный треугольник, составляет 2/9 высотыСкачать

Высота равнобедренного тр — ка опущенная на боковую сторону делит её на отрезки длиной 4 см и 16 см считая от вершины угла при основании?

Высота равнобедренного тр — ка опущенная на боковую сторону делит её на отрезки длиной 4 см и 16 см считая от вершины угла при основании.

Найти основание тр — ка.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Центр вписанной в остроугольный равнобедренный треугольник окружности делит высоту, проведенную к основанию, в отношение 5 : 3?

Центр вписанной в остроугольный равнобедренный треугольник окружности делит высоту, проведенную к основанию, в отношение 5 : 3.

Найдите радиус описанной окружности, если высота, проведенная к основанию равна 32 см.

Видео:ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию?

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию.

Найдите периметр треугольника.

Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать

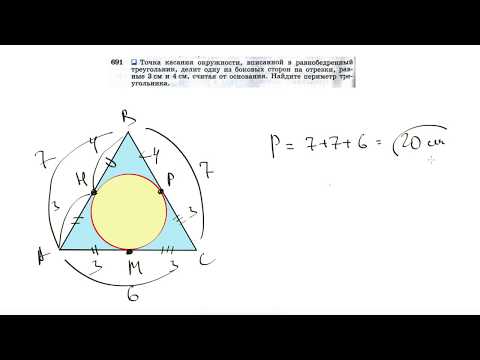
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см ; основание треугольника 12 см?

Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см ; основание треугольника 12 см.

Найти площадь этого треугольника.

Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

1) Вычислите периметр равнобедренного треугольника , если окружность, вписанная в треугольник , точкой касания делит его боковую сторону на отрезки длиной 4см и 5см, считая от основания?

1) Вычислите периметр равнобедренного треугольника , если окружность, вписанная в треугольник , точкой касания делит его боковую сторону на отрезки длиной 4см и 5см, считая от основания.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

В равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17 : 15, а боковая сторона равна 34 см?

В равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17 : 15, а боковая сторона равна 34 см.

Найдите основание треугольника.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Основание AC равнобедренного треугольника ABC равно 12?

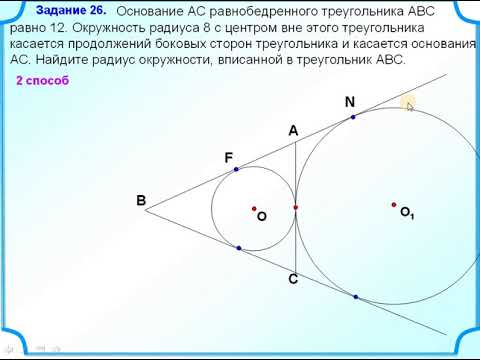
Основание AC равнобедренного треугольника ABC равно 12.

Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.

Найдите радиус окружности, вписанной в треугольник ABC.

Сторона ромба равна 32, а острый угол равен 60°.

Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка.

Каковы длины этих отрезков?

Вы открыли страницу вопроса Центр вписанной окружности делит высоту равнобедренного треугольника, опущенную на основание, на отрезки 5 см и 3 см, считая от вершины?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Возможно, кому — то пригодится решение — привожу своё : Пусть BC = AD = aBC = AD = a, тогда из условия BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5. MOMO и ONON найдём как средние линии трапеций ..

Решение 22см — одна из сторон, т. К. сумма от точки пересекч к соседним сторонам равна одной стороне. 22 — 6 = 16см — вторая сторона.

Х + х — 6 = 22 2х — 6 = 22 2х = 22 + 6 2х = 28 х = 28 / 2 х = 14 одна сторона это Х то есть 14 а вторая х — 6 то есть 14 — 6 = 8.

1) вектор а = 2i — j 2) координаты вектора c .

Вот, пожалуйста✩ ^ _ ^ Все очень просто решается по теореме Пифагора.

Решение задания приложено.

ВС = MB — MC = 18, 2 — 9, 4 = 8, 8 Ответ : 1.

1). треугольники КВА = КАD по 2 — ум сторонам и углу между ними, т. К. АD = АВ (ABCD ромб), КА — общая, углы КАВ = КАD. 2) Из равенства треугольников следует что КВ = КD.

3 и 4 не могут существовать, т. К у треугольника сумма любых двух сторон должна быть больше третьей.

Примем коэффициент подобия стороны треугольника за — х, значит : ▪одна сторона — 4х ▪ вторая сторона — 6х ▪ третья сторона — 7х ▪периметр треугольника это сумма всех его сторон, а т. К. тругольники подобные, значит стороны одного треуг. Соответстве..

Видео:Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Задача про окружность, вписанную в треугольник (Атанасян, №690)Скачать

Окружность, вписанная в равнобедренный треугольник

Если в задача дана окружность, вписанная в равнобедренный треугольник, в ее решении могут быть использованы свойства касательных и свойство биссектрисы треугольника.

Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Поскольку в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с медианой и высотой, то центр вписанной в равнобедренный треугольник окружности лежит на высоте и медиане, проведенных к основанию .

Рассмотрим две задачи на вписанную в равнобедренный треугольник окружность.

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 8:9, считая от вершины угла при основании треугольника. Найти площадь треугольника, если радиус вписанной окружности равен 16 см.

окружность (O, r) — вписанная,

F, K, M, — точки касания со сторонами AB, BC, AC,

1) Пусть k — коэффициент пропорциональности (k>0). Тогда AM=8k см, MC=9k см.

2) По свойству касательных, проведенных из одной точки,

AF=AM=8k см, CK=MC=9k см.

Так как AC=BC, то BK=AM и BF=BK=8k см.

3) Центр вписанной окружности является точкой пересечения биссектрис треугольника.

Так как ∆ ABC — равнобедренный с основанием AB, то CF — высота, медиана и биссектриса ∆ ABC.

4) Рассмотрим треугольник AFC.

∠AFC=90, AF=8k см, AC=AM+MC=17k см.

OF=r. Пусть CO=x см, тогда

CO=34 см, CF=CO+OF=34+16=50 см.

По теореме Пифагора:

Ответ: 1333 1/3 кв.см.

Центр окружности, вписанной в равнобедренный треугольник, делит высоту, проведенную к основанию, в отношении 5:4. Найти периметр треугольника, если боковая сторона меньше основания на 15 см.

Дано: ∆ ABC, AC=BC,

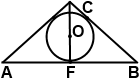
окружность (O, r) — вписанная,

CF — высота, CO:OF=5:4, AC

1) Рассмотрим ∆ ACF — прямоугольный (так как CF — высота треугольника по условию).

Центр вписанной в треугольник окружности есть точка пересечения его биссектрис.

По свойству биссектрисы треугольника,

Пусть k — коэффициент пропорциональности, тогда AC=5k см, AF=4k см, AB=2AF=8k см.

Следовательно, AC=BC=5∙5=25 см, AB=8∙5=40 см.

💥 Видео

Вписанная окружностьСкачать

Вариант 55, № 8. Радиус окружности, описанной около равнобедренного треугольникаСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать