В неравнобедренном треугольнике авс

Условие

В неравнобедренном треугольнике АВС угол BAC = 45°. Продолжение биссектрисы CD треугольника пересекает описанную около него окружность θ_(1) в точке Е. Окружность θ_(2), описанная около треугольника АDE, пересекает продолжение стороны АС в точке F.

А) Докажите, что центр окружности θ_(1) лежит на прямой FB.

Б) Найдите радиус окружности θ_(2), если известно, что АС=6, AF=2.

Решение

А) какая-то неясность с центрами и окружностями.

Центр окружности θ_(2) наверное, лежит на прямой FB.

Б)∠AСD=∠DCB — биссектриса СD делит угол пополам.
∠AВС=∠AED как вписанные углы, опирающиеся на дугу АС окружности θ _(1);
∠AED=∠AFD как вписанные углы, опирающиеся на дугу АD окружности θ _(2).

Значит, ∠AFD=∠AВС.
Δ СВF и ΔСBD равны по общей стороне СD и двум прилежащим к ней углам ( два угла в треугольниках равны, значит и третьи углы равны).
ВС=FC=FA+AC=2+6=8

По теореме синусов из треугольника АВС:
ВС/sin ∠ВАС = 2R

По теореме косинусов из Δ АВС:
BC^2=AB^2+AC^2-2AB*AC*cos45 °
8^2=AB^2+6^2-2*6*AB*sqrt(2)/2 ⇒ AB^2-6sqrt(2)*AB-28=0 ⇒

По свойству биссектрисы СD треугольника АВС:
AD:DB=АС:СВ=6:8 ⇒ [b]AD:DB=3:4[/b] и AD=(3/4)BD

Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

В прямоугольном неравнобедренном треугольнике АВС из вершины С прямого угла проведены высота СН, медиана СМ и биссектриса СL?

Геометрия | 5 — 9 классы

В прямоугольном неравнобедренном треугольнике АВС из вершины С прямого угла проведены высота СН, медиана СМ и биссектриса СL.

А) Докажите, что CL является биссектрисой угла МСН.

Б) Найдите длину биссектрисы CL, если СН = 3, СМ = 5.

1) Пусть катет AC&gt ; BC

Медиана в прямоугольном тр — ке является радиусом описанной окружности⇒

CM = AM = BM⇒Тр — ник CMB — равнобедренный⇒угол MBC равен углу MCB = α — введем такое обозначение.

СH перпенд AB⇒угол CHB равен 90 гр

CL — биссектриса⇒угол ACL равен углу BCL = 45 гр

Найдем углы MCL и LCH и покажем, что они равны

Угол LCH = угол BCL — угол BCH

Из прямоуг тр — ка CHB угол BCH = 90 — α⇒

Угол LCH = 45 — (90 — α) = α — 45

Угол MCL = угол MCB — угол BCL = α — 45⇒

Угол LCH = Угол MCL⇒CL — биссектриса угла МСН

2) Биссектриса делит сторону на части , пропорциональные прилежащим сторонам⇒CM / CH = ML / LH = 5 / 3

Пусть ML = 5x ; LH = 3x⇒MH = 8x⇒

Из прямоуг тр — ка MHC имеем :

CM ^ 2 = CH ^ 2 + MH ^ 2⇒9 + 64x ^ 2 = 25⇒64x ^ 2 = 16⇒x ^ 2 = 1 / 4⇒x = 1 / 2⇒LH = 3 / 2

CL ^ 2 = CH ^ 2 + LH ^ 2⇒CL ^ 2 = 9 + 9 / 4 = 45 / 4⇒CL = √45 / 4 = 3√5 / 2

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Из вершины прямого угла прямоугольного треугольника проведены биссектриса и высота , угол между которыми 19 градусов ?

Из вершины прямого угла прямоугольного треугольника проведены биссектриса и высота , угол между которыми 19 градусов .

Найти острые углы треугольника .

Видео:№257. В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120°Скачать

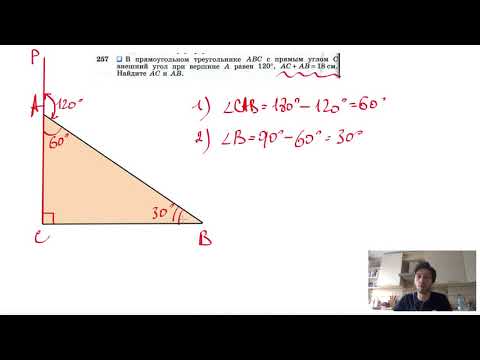
В прямоугольном треугольнике АВС с прямым углом С проведена биссектриса ВD угла В, СD = 6, СВ = 12?

В прямоугольном треугольнике АВС с прямым углом С проведена биссектриса ВD угла В, СD = 6, СВ = 12.

Найдите гипотенузу треугольника АВС.

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

В прямоугольном треугольнике АВС с прямым углом С проведены биссектрисы АМ и ВN, пересекающиеся в точке О?

В прямоугольном треугольнике АВС с прямым углом С проведены биссектрисы АМ и ВN, пересекающиеся в точке О.

Найдите величину угла АОВ.

Видео:ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

Докажите, что если в треугольнике АВС сторона АВ в два раза больше АС, то медиана, входящая из вершины С, перпендикулярна биссектрисе угла А?

Докажите, что если в треугольнике АВС сторона АВ в два раза больше АС, то медиана, входящая из вершины С, перпендикулярна биссектрисе угла А.

Видео:В прямоугольном треугольнике ABC с прямым углом C известны катетыСкачать

В прямоугольном треугольнике АВС проведена биссектриса АF?

В прямоугольном треугольнике АВС проведена биссектриса АF.

Найдите величину угла АFС.

Видео:Геометрия из № 23 ОГЭ В прямоугольном треугольнике ABC с прямым углом С известны катеты: АС = 6Скачать

В прямоугольном треугольнике один из углов равен 50 градусов?

В прямоугольном треугольнике один из углов равен 50 градусов.

Найдите угол между высотой и биссектрисой, проведенных из вершины прямого угла.

Видео:В прямоугольном треугольнике ABC ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Угол между биссектрисой и высотой прямоугольного треугольника, которые проведены из вершины прямого угла, равен 15°?

Угол между биссектрисой и высотой прямоугольного треугольника, которые проведены из вершины прямого угла, равен 15°.

Вычислите углы треугольника.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

АМ — биссектриса прямого угла равнобедренного прямоугольного треугольника АВС?

АМ — биссектриса прямого угла равнобедренного прямоугольного треугольника АВС.

Найдите углы треугольника АВМ.

Видео:Задача 6 №27350 ЕГЭ по математике. Урок 42Скачать

В прямоугольном треугольнике проведены высота и биссектриса прямого угла равны 5 и 7?

В прямоугольном треугольнике проведены высота и биссектриса прямого угла равны 5 и 7.

Найдите площадь треугольника.

Видео:ОГЭ по математике. Задача 9-2Скачать

Один из углов прямоугольного треугольника равен 49 градусам?

Один из углов прямоугольного треугольника равен 49 градусам.

Найдите угол между биссектрисой высотой , проведенных из вершины прямого угла.

На этой странице сайта вы найдете ответы на вопрос В прямоугольном неравнобедренном треугольнике АВС из вершины С прямого угла проведены высота СН, медиана СМ и биссектриса СL?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Одно из свойствы треугольника : Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон : a Существует ли четырех угольник зл сторонами 2см 6 см 9см 17см?

Видео:Высота в прямоугольном треугольнике | Математика ЕГЭ 2024 #егэпрофиль #профильСкачать

В прямоугольном неравнобедренном треугольнике АВС из верхушки С прямого угла проведены

В прямоугольном неравнобедренном треугольнике АВС из верхушки С прямого угла проведены вышина СН, медиана СМ и биссектриса СL.
а) Обоснуйте, что CL является биссектрисой угла МСН.
б) Найдите длину биссектрисы CL, если СН=3, СМ=5

• Шурик Блеклов
• Геометрия 2019-07-18 20:59:06 0 1

1) Пусть катет ACgt;BC
Медиана в прямоугольном тр-ке является радиусом описанной окружности
CM=AM=BMТр-ник CMB — равнобедренныйугол MBC равен углу MCB= — введем такое обозначение.
СH перпенд ABугол CHB равен 90 гр
CL — биссектрисаугол ACL равен углу BCL=45 гр
Найдем углы MCL и LCH и покажем, что они одинаковы
Угол LCH =угол BCL — угол BCH
Из прямоуг тр-ка CHB угол BCH=90-
Угол LCH =45-(90-)=-45
Угол MCL =угол MCB — угол BCL=-45
Угол LCH=Угол MCLCL — биссектриса угла МСН
2) Биссектриса разделяет сторону на доли , пропорциональные прилежащим сторонамCM/CH=ML/LH=5/3
Пусть ML=5x; LH=3xMH=8x
Из прямоуг тр-ка MHC имеем:
CM^2=CH^2+MH^29+64x^2=2564x^2=16x^2=1/4x=1/2LH=3/2
CL^2=CH^2+LH^2CL^2=9+9/4=45/4CL=45/4=35/2
Ответ: 35/2

🔥 Видео

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

пропорциональные отрезки в ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ 8 классСкачать

Геометрия В прямоугольном треугольнике ABC проведена высота CH из вершины прямого углаСкачать

Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

🔥 Свойства МЕДИАНЫ #shortsСкачать