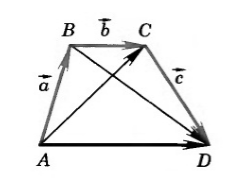
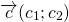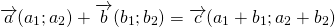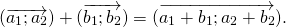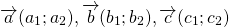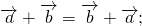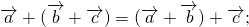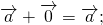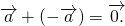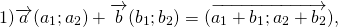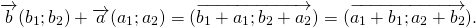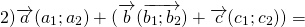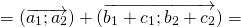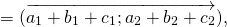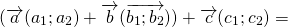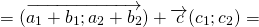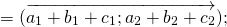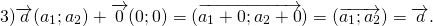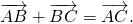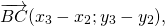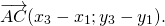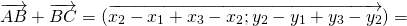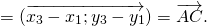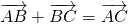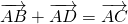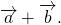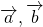Сумма векторов
Свойства сложения векторов:
Для любых векторов
3) свойство прибавления нулевого вектора:
4) сумма противоположных векторов равна нулевому вектору:
Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:
Так как соответствующие координаты равны, то эти векторы равны.
(О сложении векторов)
Каковы бы ни были точки A, B, C, имеет место векторное равенство:
Что и требовалось доказать.
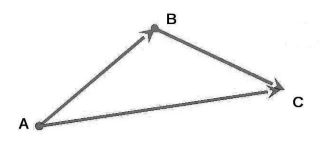
Правило треугольника построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.
(то есть это правило следует из теоремы о сложении векторов).
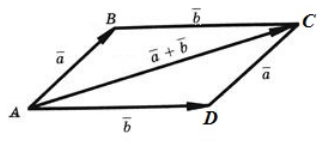
Правило параллелограмма построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.
При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.
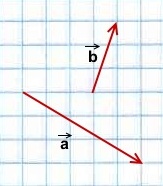
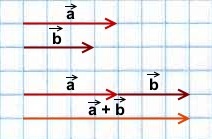
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора
Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).
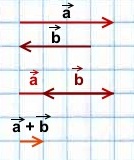
2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы
от общего начала.
Достроим на этих векторах параллелограмм.
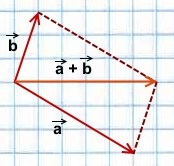
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.
2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.
Фактически в обоих случаях мы используем правило треугольника сложения векторов:
от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.
Из неравенства треугольника следует ещё два свойства сложения векторов:
Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Сложение векторов
Часть математических и физических задач содержит необходимость математических действий с векторами (сложение и вычитание).
Проиллюстрируем сложение. Пусть даны вектора и , попытаемся найти вектор .
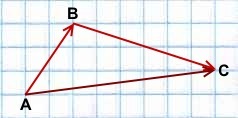
Способ 1. Метод сложения треугольником
Возьмём необходимые вектора и параллельным переносом совместим конец первого вектора ( ) и начало второго ( ) (рис. 1)
Рис. 1. Сложение векторов (правило треугольника)
Тогда вектор, соединяющий начальную точку первого вектора ( ) и конец второго ( ), является вектором ( ).
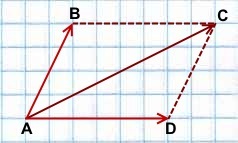
Способ 2. Метод сложения параллелограммом
Возьмём необходимые вектора и параллельным переносом совместим начало первого вектора ( ) и начало второго ( ) (рис. 2). Параллельным переносом совместим конец каждого вектора с началом другого.
Рис. 2. Сложение векторов (правило параллелограмма)
Тогда вектор, соединяющий общую начальную точку первого ( ) и второго ( ) векторов и общий конец данных векторов, является вектором суммы ( ).
Вывод: в ряде задач, где присутствуют несколько однородных векторных физических величин, часто необходимо найти общий вектор (общую скорость, равнодействующую силу, полный вектор магнитной индукции или электрической напряжённости поля). Тогда необходимо сначала сложить вектора, а потом найти модуль получившегося вектора.Чаще всего первый метод используется в кинематике (сложение скоростей). Второй метод часто используют в динамике.
Видео:Эндшпиль. Правило треугольникаСкачать

Сложение векторов. Как найти сумму векторов
Вы будете перенаправлены на Автор24
Видео:СЛОЖЕНИЕ ВЕКТОРОВ закон правило треугольника 9 класс АтанасянСкачать

Откладывание вектора от данной точки
Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Введем следующую теорему:
От любой точки $K$ можно отложить вектор $overrightarrow$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
В этом случае, очевидно, что искомый вектор — вектор $overrightarrow$.
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сложение векторов. Правило треугольника
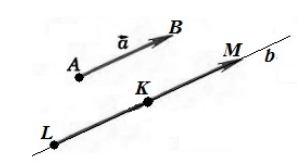
Пусть нам даны векторы $overrightarrow$ и $overrightarrow$.
Рисунок 3. Сумма векторов
Готовые работы на аналогичную тему
Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.
Из этого правила следует несколько свойств сложения двух векторов:
Для любого вектора $overrightarrow$ выполняется равенство
Для любых произвольных точек $A, B и C$ выполняется равенство
Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.
Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Правило параллелограмма
Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.
Доказательство.
Переместительный закон:
Рисунок 4. Иллюстрация переместительного закона
Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $left|overrightarrow+overrightarrowright|и |overrightarrow+overrightarrow|$.
Сочетательный закон:
Рисунок 5. Иллюстрация сочетательного закона
Из свойства правила треугольника $overrightarrow+overrightarrow=overrightarrow$, получим:
Теорема доказана.
Видео:Сложение векторов. 9 класс.Скачать

Пример задачи на сложение векторов
Дан четырехугольник $ABCD$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Доказательство.
Воспользуемся свойством правила треугольника $overrightarrow+overrightarrow=overrightarrow$, получим:
ч. т. д.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 01 04 2021
🎦 Видео
Вычислить определитель 3 порядка. Правило треугольникаСкачать

8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

Треугольники. 7 класс.Скачать

Сумма двух векторов. Правило треугольника. Законы сложения векторов. Правило параллелограмма.Скачать

83. Законы сложения векторов. Правило параллелограммаСкачать

Сложение нескольких векторов. Правило многоугольникаСкачать

Урок 4. Векторы. Сложение векторов. Правило треугольника. Правило параллелограмма.Скачать
Урок 6. Правило "Треугольника"Скачать

Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Позиция артикля - правило треугольникаСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Сложение векторов по правилу треугольника и по правилу параллелограмма. Геометрия 8-9 классСкачать

ВЕКТОРЫ: сложение и вычитание векторов, правило треугольника, законы сложения и разность векторовСкачать

Сумма векторов. Правило треугольника и правило параллелограммаСкачать