Угол 120 в треугольнике

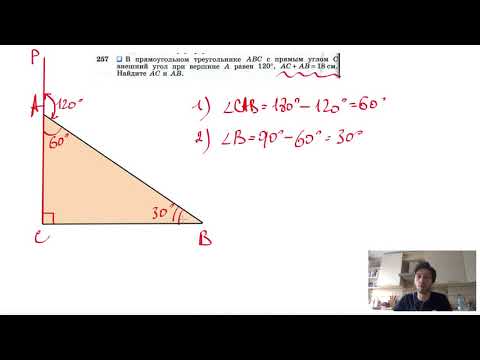
Видео:№257. В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120°Скачать

Синус, косинус и тангенс угла 2π/3 радиан

Напомним себе, что 2π/3 в градусах — это 120 градусов. ( 2 * 180 / 3 = 120 ). Таким образом, найти значение тригонометрической функции для угла 2π/3 и для ула 120 градусов — это одно и то же.

Как найти значения тригонометрических функций для угла 120 градусов

Найдем значения синуса, косинуса и тангенса для угла 120 градусов аналитическим способом.
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 120 градусов — задача сложная. Однако, это не совсем так.
Прежде всего, мы должны обратить внимание, что для углов, значения которых превышают 90 градусов, у нас есть формулы приведения к углу, меньшему 90 градусов.

Поэтому, для начала, представим себе угол в 120 градусов как (90 + 30)
Тогда
sin ( 90 + α ) = cos α
sin 120 = sin( 90 + 30 ) = cos 30

cos ( 90 + α ) = — sin α
cos 120 = cos( 90 + 30 ) = -sin 30

tg ( 90 + α ) = -ctg α
tg 120 = tg( 90 + 30 ) = -ctg 30

Теперь можно посмотреть значения в таблицах синуса, косинуса и тангенса 120 градусов, который преобразован в значения тригонометрических функций синуса, косинуса и тангенса угла 30 градусов.

В уроке по ссылке можно посмотреть как вычислить значения тригонометрических функций для угла 30 градусов.

В итоге получаем:

Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 120 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств.

См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).

Ниже приведены также значения тригонометрических функций для угла 120 градусов в виде десятичной дроби с четырьмя знаками после запятой.

Видео:№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:Построение угла 120 градусов с помощью циркуля и линейки.Скачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:В равнобедренном треуг один из углов 120 , основание 4см, найдите высоту проведенную к бок сторонеСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Видео:16 заание ОГЭ . 16.3.4. Равнобедренные треугольникиСкачать

Остроугольный, прямоугольный и тупоугольный треугольники.

Виды треугольников

Остроугольный треугольник — это треугольник,
в котором все углы острые.

Прямоугольный треугольник — это треугольник,
в котором один из углов прямой.

Тупоугольный треугольник — это треугольник,
в котором один из углов тупой.

Как определить вид треугольника

Для того, чтобы понять какой треугольник — остроугольный, прямоугольный или тупоугольный
нужно знать какая градусная мера у углов в треугольнике.

Если один из углов в треугольнике прямой, значит треугольник прямоугольный. Все углы острые в треугольнике — значит треугольник остроугольный. Если в треугольнике один из углов тупой, значит треугольник тупоугольный.

В произвольном треугольнике все углы острые, или два угла острые, а третий прямой или тупой. Если в треугольнике вам известно, что один углов тупой или прямой, значит сумма двух других углов не больше 90 градусов.

В прямоугольном треугольнике стороны напротив острых углов называются катетами, а сторона напротив прямого угла называется гипотенузой.

Градусные меры острого, тупого, прямого углов в треугольниках

Чтобы понять как называется угол и как называется треугольник с этими углами — надо знать его градусную меру:

1. Острый угол в любом из треугольников не больше 90 градусов.
2. Прямой угол в любом из треугольников равен 90 градусам.
3. Тупой угол в любом из треугольников больше 90 градусов, но меньше 180 градусов.

📺 Видео

Геометрия Сумма двух сторон треугольника образующих угол 120 равна 8 см а длина третьей стороныСкачать

№707. Угол, противолежащий основанию равнобедренного треугольника, равен 120°, боковая сторонаСкачать

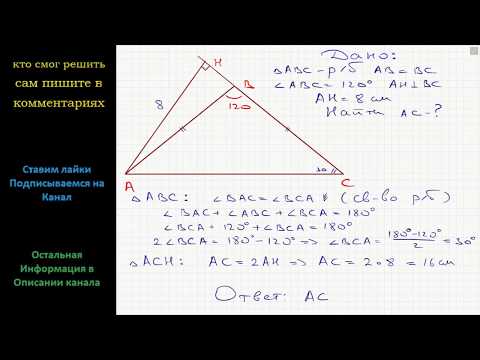
Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Как начертить три линии под 120 градусов и шестиугольникСкачать

Геометрия Две стороны треугольника угол между которыми равен 120 относятся как 5:3 Найдите стороныСкачать

Геометрия Угол при вершине равнобедренного треугольника равен 120, а высота, проведенная к основаниюСкачать

Геометрия Угол, противолежащий основанию равнобедренного треугольника, равен 120, а высотаСкачать

Построение углов заданной градусной мерыСкачать

Геометрия Найти площадь равнобедренного треугольника с углом 120, если радиус вписанного круга равенСкачать

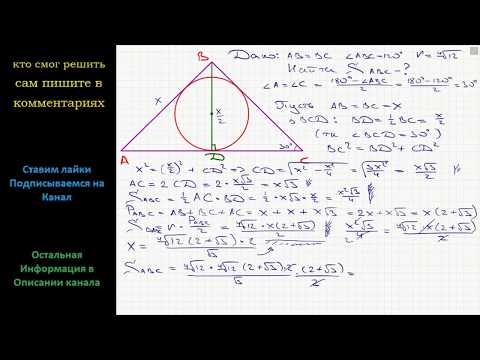
Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Геометрия В треугольнике ABC известно что AB = BC, угол ABC =120 На продолжении отрезка AB за точкуСкачать

Геометрия В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BDСкачать

Геометрия В равнобедренный треугольник с углом 120 при вершине и боковой стороной а вписанаСкачать