Углы связанные с окружностью тест (6 видео)

Тест по теме «Углы, связанные с окружностью. Свойства хорд и секущих»

Тест предназначен для проверки уровня обученности учащихся 8 класса по теме » Углы, связанные с окружностью. Свойства хорд и секущих.» Тест ориентирован на учебник Л.С. Атанасяна и др. «Геометрия. 7-9 классы», но может быть использован учителями, работающими по другим учебникам.

Тест предназначен для учителей математики; его могут использовать и учащиеся 8 класса для подготовки к контрольной работе и зачету, а также учащиеся 9 для подготовки к экзамену по математике.

Содержание

Просмотр содержимого документа «Тест по теме «Углы, связанные с окружностью. Свойства хорд и секущих»»
Тест по геометрии по теме » Углы и отрезки, связанные с окружностью». 10 класс
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Краткое описание документа:
Дистанционное обучение как современный формат преподавания
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Математика: теория и методика преподавания в образовательной организации
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Дистанционные курсы для педагогов
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
Углы, связанные с окружностью
Вписанные и центральные углы
Теоремы о вписанных и центральных углах
Теоремы об углах, образованных хордами, касательными и секущими
Доказательства теорем об углах, связанных с окружностью
📺 Видео

Просмотр содержимого документа
«Тест по теме «Углы, связанные с окружностью. Свойства хорд и секущих»»

Свойства хорд и секущих

1. Стороны вписанного угла содержат

хорды
касательную и хорду
касательные

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Тест по геометрии по теме » Углы и отрезки, связанные с окружностью». 10 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Углы, связанные с окружностьюСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Тест по геометрии по теме «Углы и отрезки, связанные с окружностью». 10 класс.

Угол АСВ на 38 0 меньше угла АОВ. Найдите сумму углов АОВ и АСВ

А)96 0

2. МР-диаметр, О-центр окружности. ОМ=ОК=МК. Найдите угол РКО

3. Угол АВС- вписанный, угол АОС-центральный. Найдите угол АВС, если угол АОС равен 126 0 .

4. К D и МС- хорды одной окружности, причём Е-точка их пересечения. Найдите угол С DE , если угол DEM в 4 раза больше угла DEC , а угол CMK на 26 0 больше угла DEC .

5. КВ=12 см, КС=30 см, Р(АКВ)=28 см. Найти Р(СК D )

6. КМ и С D -хорды, Е-точка их пересечения, СЕ=6 см, Е D =8 см, КЕ на 8 см меньше ЕМ. Найдите КМ.

7. АВ=20 см, АС=4 см, АЕ =16 см. Найти DE .

8. АВ- касательная к окружности. Найдите А D , если АВ=6, CD =5

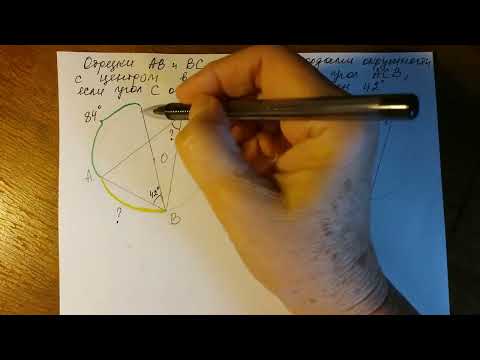
Угол МСК на 34 0 меньше угла МОК. Найдите сумму углов МСК и МОК.

2. АС-диаметр окружности, О-её центр. ОС=ОВ=ОА. Найдите угол ОСВ.

3. О-центр окружности. Угол Β =136 0 . Найдите α.

4. АС и BD –хорды одной окружности, причем Е-точка их пересечения. Угол СED в 9 раз больше угла ВЕС, а угол DAE на 61 0 больше угла ВЕС. Найдите угол СВЕ.

5. МК=16, NC =24, Р(МКЕ)=28. Найти Р( NCE ).

6. BD и СЕ-хорды одной окружности, А-точка их пересечения, АС=6 дм, АЕ=12 дм, АВ на 1 дм меньше А D . Найдите BD .

7. СК=16, СР=6, СМ=24. Найти DM .

8. МК- касательная к окружности. Найдите ВМ, если МК=8 см, ВС=12 см.

Краткое описание документа:

Данный тест предназначен для проверки знаний, полученных при изучении раздела » Углы и отрезки, связанные с окружностью» в 10 классе. На момент начала изучения раздела десятиклассникам известно, что вписанный угол измеряется половиной дуги, на которую он опирается, а так же известно, что центральный угол измеряется дугой, на которую он опирается. После изучения данного раздела, имея в багаже знаний теорему про угол между касательной и хордой, теорему о произведении отрезков одной из двух пересекающихся хорд, теорему о секущей, пересекающей окружность, учащиеся могут выполнить данный тест, что позволит учителю понять усвоение данной темы детьми.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 939 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 318 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 694 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 479 045 материалов в базе

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Дистанционные курсы для педагогов

Другие материалы

30.09.2020
217

30.09.2020
566

30.09.2020
213

30.09.2020
279

30.09.2020
198

30.09.2020
197

30.09.2020
306

30.09.2020
210

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

05.01.2015 1832 —> —> —> —>
DOCX 78.1 кбайт —> —>
Рейтинг: 5 из 5
Оцените материал:

Настоящий материал опубликован пользователем Шальнева Наталия Ивановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На проекте: 7 лет
Подписчики: 0
Всего просмотров: 14533
Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Углы, связанные с окружностьюСкачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Первые результаты по сокращению отчетности у учителей ожидаются осенью

Время чтения: 1 минута

В Госдуме призвали обсуждать на школьных уроках тему опасности абортов

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Китае приняли закон о сокращении нагрузки на школьников

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России могут создать комиссию по поддержке одаренных детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать

Углы, связанные с окружностью

Вписанные и центральные углы

Углы, образованные хордами, касательными и секущими

Доказательства теорем об углах, связанных с окружностью

Видео:8 класс. Углы, связанные с окружностью.Скачать

Вписанные и центральные углы

Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Теоремы о вписанных и центральных углах

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Фигура	Рисунок	Теорема
Вписанный угол
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Вписанный угол		Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды
Вписанный угол		Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Окружность, описанная около прямоугольного треугольника

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Видео:Геометрия. Углы и отрезки, связанные с окружностью.Скачать

Теоремы об углах, образованных хордами, касательными и секущими

Вписанный угол

Окружность, описанная около прямоугольного треугольника

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами
Угол, образованный секущими, которые пересекаются вне круга
Угол, образованный касательной и хордой, проходящей через точку касания
Угол, образованный касательной и секущей
Угол, образованный двумя касательными к окружности

Угол, образованный пересекающимися хордами хордами

Формула:

Угол, образованный секущими секущими , которые пересекаются вне круга

Формула:

Угол, образованный касательной и хордой хордой , проходящей через точку касания

Формула:

Угол, образованный касательной и секущей касательной и секущей

Формула:

Угол, образованный двумя касательными касательными к окружности

Формулы:

Видео:Теоремы об отрезках, связанных с окружностью. Урок 22. Геометрия 11 классСкачать

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство