Циркуляция вектора магнитной индукции окружность (8 видео)

Поток и циркуляция вектора магнитной индукции

В природе нет магнитных зарядов, вследствие чего линии В не имеют ни начала, ни конца — они либо замкнуты, либо уходят в бесконечность. Поэтому в соответствии с формулой (1.24) поток Ф_в вектора В через замкнутую поверхность должен быть равен нулю. Следовательно, для любого магнитного потока и произвольной замкнутой поверхности S:

Эта формула выражает теорему Гаусса для вектора В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Отсутствие начала и конца магнитных линий означает, что дивергенция вектора В всюду равна нулю:

Найдём циркуляцию вектора В. По определению циркуляция равна интегралу

где d(. — элемент замкнутого контура, по которому производится интегрирование.

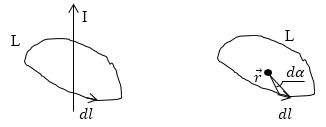
Проще всего вычислить интеграл (5.43) в случае прямого тока. Пусть замкнутый контур лежит в плоскости, перпендикулярной к проводу, по которому за чертёж течёт ток I (рис. 5.10). В каждой точке контура вектор В направлен по касательной к окружности, проходящей через эту точку. Представим Bdl в виде В ? d?_B (d?_B -проекция d? на направление вектора В).

Из рисунка следует, что di_B равна bda , где b — расстояние от провода с током до dl; da — угол, на который поворачивается радиальная прямая при перемещении вдоль контура на отрезок dl. Подставив в (5.43) это значение d?_B и выражение (5.27) для В, получим:

Содержание

Закон Био-Савара. Теорема о циркуляции
Закон Био–Савара
Теорема о циркуляции вектора магнитной индукции
Теорема о циркуляции вектора индукции магнитного поля
Интегральная форма теоремы о циркуляции
Готовые работы на аналогичную тему
Дифференциальная форма теоремы о циркуляции
🔥 Видео

Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Закон Био-Савара. Теорема о циркуляции

Французские ученые Ж. Био и Ф. Савар в 1820 -м году проводили эксперименты над магнитным полем постоянных токов. Физики доказали, что индукция магнитного поля проходящих по проводнику токов зависит от совместного действия всех участков данного проводника. Работа магнитного поля основана на принципе суперпозиции.

Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.

Индукция B → проводника с током представлена, как векторная сумма элементарных индукций ∆ B → вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?

Видео:Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать

Закон Био–Савара

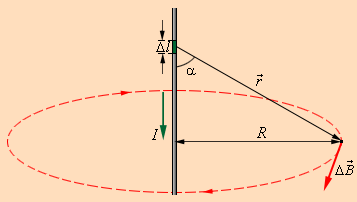
Закон Био-Савара определил вклад ∆ B → в магнитную индукцию B → результативного магнитного поля, образуемый маленьким участком Δ l проводника с током I .

∆ B = μ 0 · I · ∆ l · sin α 4 π r 2 .

В формуле r – это расстояние от заданного участка Δ l до точки наблюдения, α – это угол между направлением на точку наблюдения и направлением тока на заданном участке, μ 0 – это магнитная постоянная.

Используя правило буравчика, определим направление вектора ∆ B → : оно указывает на ту сторону, в которую вращается рукоятка буравчика при его поступательном движении вдоль тока. Рисунок 1 . 17 . 1 наглядно показывает закон Био-Савара с применением магнитного поля прямолинейного проводника с током. Если сложить (интегрировать) вклады в магнитное поле всех участков проводника с током, тогда получим формулу для магнитной индукции поля прямого тока:

Рисунок 1 . 17 . 1 . Иллюстрация закона Био–Савара.

С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:

где R – это радиус кругового проводника.

Чтобы определить направление вектора B → тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.

Видео:Теорема о циркуляции вектора магнитной индукции. Магнитный поток.Скачать

Теорема о циркуляции вектора магнитной индукции

Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.

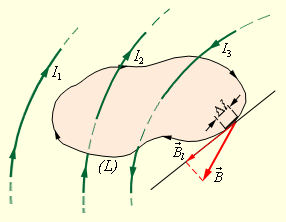
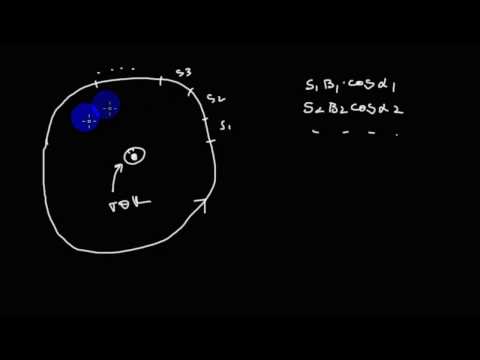
Объясним, что означает циркуляция вектора B → . Допустим, в пространстве с магнитным полем существует какой-то условный замкнутый контур, а также положительное направление его обхода. Тогда, на каждом отдельном маленьком участке Δ l данного контура определяется касательная составляющая B l вектора B → в этом месте, то есть определяется проекция вектора B → на направление касательной к заданному участку контура. Рисунок 1 . 17 . 2 наглядно демонстрирует это.

Рисунок 1 . 17 . 2 . Замкнутый контур ( L ) с заданным направлением обхода. Изображение токов I 1 , I 2 и
I 3 , создающих магнитное поле.

Циркуляция вектора B → – это сумма произведений B l ∆ l , взятая по целому контуру L : B → = ∑ ( L ) B l ∆ l.

Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур L тем временем, как остальные токи находятся в стороне от контура.

Согласно теореме о циркуляции, циркуляция вектора B → магнитного поля постоянных токов по любому из контуров L все время определяется, как произведение магнитной постоянной μ 0 на сумму всех токов:

∑ ( L ) B l ∆ l = μ 0 ∑ l i.

На рисунке 1 . 17 . 2 продемонстрирован пример с несколькими проводниками с токами, образующими магнитное поле. Ток I 2 и ток I 3 пронзают контур L в противоположных направлениях, им приписываются различные знаки. Положительным является ток, который связан с заданным направлением обхода контура по правилу буравчика.

Значит, I 3 > 0 , а I 2 0 . Ток I 1 не пронзает контур L .

Теорема о циркуляции в этом примере математически выражается следующей формулой:

∑ ( L ) B l ∆ l = μ 0 ( I 3 — I 2 ) .

Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.

Самый простой пример использования теоремы о циркуляции – это вывод формулы магнитного поля прямолинейного проводника с током. С учетом симметрии в этой задаче контуром L лучше выбрать окружность какого-то радиуса R , лежащую в перпендикулярной проводнику плоскости. Центр окружности задан в какой-то точке проводника. Из-за симметрии вектор B → направляется по касательной ( B l = B ) , а его модуль имеет одинаковое значение по всей окружности. Использование теоремы о циркуляции приводит к выражению:

∑ ( L ) B l ∆ l = 2 π R B = μ 0 I ,

отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.

Из данного примера видно, что теорема о циркуляции вектора магнитной индукции B → можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.

Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.

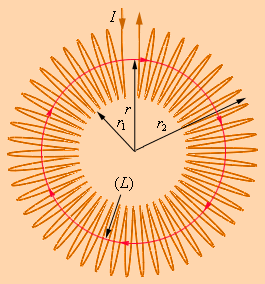
Рассмотрим одну из них – это задачу расчета поля тороидальной катушки (рисунок 1 . 17 . 3 ).

Рисунок 1 . 17 . 3 . Использование теоремы о циркуляции к тороидальной катушке.

Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.

Одна линия индукции какого-то радиуса r 1 ≤ r r 2 представлена на рисунке 1 . 17 . 3 . Используем теорему о циркуляции для контура L в виде окружности, которая совпадает с линией индукции магнитного поля, изображенной на рисунке 1 . 17 . 3 . Опираясь на соображения о симметрии, делаем вывод, что модуль вектора B → имеет одинаковое значение по всей линии. Исходя из теоремы о циркуляции, запишем:

B · 2 π r = μ 0 I N ,

где N – это полное количество витков, а I – это ток, протекающий по виткам катушки. Значит, B = μ 0 I N 2 π r .

Так, модуль вектора магнитной индукции в тороидальной катушке находится в зависимости от радиуса r . При условии, что сердечник катушки тонкий, то есть r 2 – r 1 ≪ r , тогда магнитное поле внутри катушки почти однородное.

Величина n = N 2 π r – это количество витков на единицу длины катушки. Следовательно, B = μ 0 I n .

Сюда не относится радиус тора, потому оно действует и в предельном случае r → ∞ .

Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.

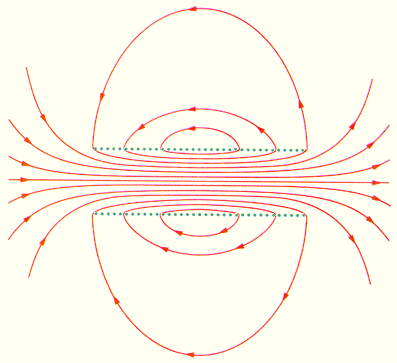
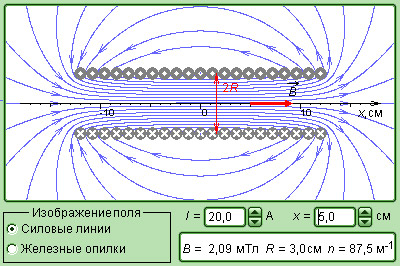
На рисунке 1 . 17 . 4 представлено магнитное поле катушки конечной длины. Обращаем внимание, что в центре катушки магнитное поле почти однородное и намного сильнее, чем снаружи. Это объясняется густотой линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле полностью находится внутри него.

Рисунок 1 . 17 . 4 . Магнитное поле катушки конечной длины. В центральной части соленоида магнитное поле почти однородное и существенно больше по модулю поля вне катушки.

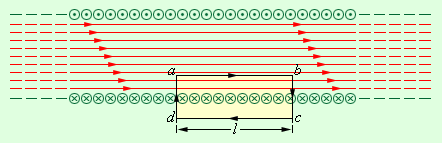
В случае с бесконечно длинным соленоидом соотношение для модуля магнитной индукции получаем прямо из теоремы о циркуляции, применяя ее к прямоугольному контуру, изображенному на рисунке 1 . 17 . 5 .

Рисунок 1 . 17 . 5 . Теорема о циркуляции при расчете магнитного поля бесконечно длинного соленоида.

Проекция вектора магнитной индукции на направление обхода контура a b c d только на стороне a b отлична от 0 . Значит, циркуляция вектора B → по контуру равняется B l , где l – это длина стороны a b . Количество витков соленоида, пронзающих контур a b c d , равняется n · l , где n – это количество витков на единицу длины соленоида, а полный ток, пронзающий контур, равняется I n l . Из теоремы о циркуляции, B l = μ 0 I n l .

Отсюда B = μ 0 I n .

Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.

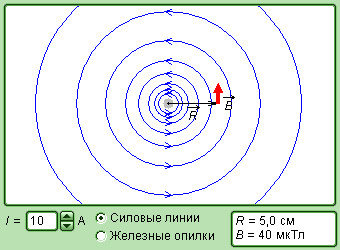
Рисунок 1 . 17 . 6 . Модель магнитного поля кругового витка с током.

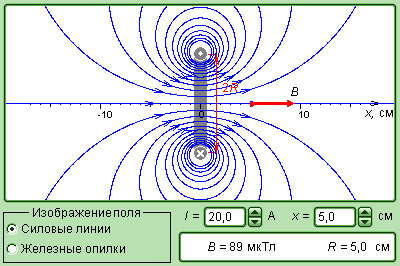
Рисунок 1 . 17 . 7 . Модель магнитного поля прямого тока.

Рисунок 1 . 17 . 8 . Модель магнитного поля соленоида.

Видео:Лекция 2.3. Теорема о циркуляцииСкачать

Теорема о циркуляции вектора индукции магнитного поля

Вы будете перенаправлены на Автор24

Видео:53. Теорема о циркуляции вектора индукцииСкачать

Интегральная форма теоремы о циркуляции

Линии индукции магнитного поля, которое возникает вокруг постоянного тока, который течет по прямолинейному длинному проводнику — концентрические окружности с центрами на линии тока. Интеграл вида $ointlimits_L<overrightarrowdoverrightarrow> $- циркуляция вектора $overrightarrow$ по замкнутому контуру L. Найдем $ointlimits_L<overrightarrowdoverrightarrow>$ по некоторому замкнутому контуру вокруг тока I (рис. 1).

Линии магнитной индукции лежат в плоскостях перпендикулярных линии тока I, контур L выбираем в плоскости одной из линий $overrightarrow.$ Используем рис.1, получим:

Обозначим $left(widehat<overrightarrowdoverrightarrow>right)=alpha $, тогда имеем:

По условию магнитное поле создает бесконечно длинный прямой проводник с током, индукцию поля которого мы знаем, и запишем в точке на расстоянии r от проводника как:

Подставим (3) и (2) в формулу (1), получим:

Теперь найдем циркуляцию вектора магнитной индукции, используя (4), получим:

где использовано то, что для замкнутого контура, который окружает начало координат:

Из полученного результата в (5) видим, что циркуляция вектора магнитной индукции по замкнутому контуру вокруг тока не зависит от вида контура и определена только силой тока. В том случае если контур ток не охватывает, то циркуляция вектора индукции равна нулю.

Тогда теорема о циркуляции для нескольких токов формулируется следующим образом:

Циркуляция индукции магнитного поля постоянных токов по произвольному замкнутому контуру равна алгебраической сумме токов, которые пронизывают этот контур.

Готовые работы на аналогичную тему

В математическом виде данная формулировка выглядит как уравнение:

где через I — обозначают полный ток (алгебраическая сумма всех токов, охватываемых контуром). Теорема о циркуляции еще называется законом полного тока. Надо иметь в виду, что циркуляция вектора $overrightarrow$ по замкнутому контуру равна нулю не только в случае отсутствия токов, которые пронизывают заданный контур, но и если токи текут в противоположных направлениях и в сумме дают ноль. В формуле (7) знак тока учитывается по правилу правого винта. Этот закон мы получили для прямого бесконечного проводника, но он справедлив и для произвольного тока.

Видео:Электродинамика | теорема о циркуляции магнитной индукции | 1Скачать

Дифференциальная форма теоремы о циркуляции

Пусть S — поверхность, которую охватывает контур L. Положительная нормаль к поверхности связана с направлением обхода контура L правилом правого винта. Силу полного тока, который течет через поверхность S можно записать как:

где $overrightarrow$ — объёмная плотность тока. В таком случае теорему о циркуляции запишем как:

По теореме Стокса можно записать, что:

Равенство (11) выполняется для любой поверхности, следовательно, подынтегральное выражение также равно нулю:

[rotoverrightarrow-_0overrightarrow=0to rotoverrightarrow=_0overrightarrow left(12right).]

Равенство (12) дифференциальная форма теоремы о циркуляции. Она справедлива для произвольного поля в каждой точке.

Напомним, что теорема о циркуляции в виде (7) и (12) записана для поля в вакууме и стационарных токов.

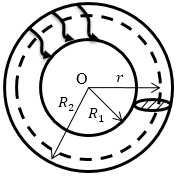
Задание: Тороид имеет каркас в виде тора и на него намотан проводник, по которому течет ток. Магнитное поле данной конфигурации токов сосредоточено в основном внутри тороида. Поле имеет осевую симметрию. Силовые линии магнитного поля тороида представляют собой окружности с центром на оси тороида. Используя теорему о циркуляции, найдите магнитное поле внутри тороида (рис.2) (B(r)). Если сила тока в нем равна I. N — число витков тороида.

В качестве контура циркуляции выберем силовую линию в виде окружности радиуса r (рис.2). Запишем, что циркуляция вектора индукции магнитного поля вдоль выбранной окружности равна:

[ointlimits_L<overrightarrowdoverrightarrow>=B2pi r left(1.1right).]

Тогда теорема о циркуляции предстанет в виде:

где $N$ — число витков с током. Выразим модуль вектора индукции, получим:

Задание: Какова циркуляция вектора индукции вдоль контура, который охватывает токи $I_1=5 A, I_2=6 A$, $I_3=10 A$, если первые два тока текут в одном направлении, третий в противоположном.

По теореме о циркуляции:

Для нашего случая имеем:

Проведем вычисление, получим:

[ointlimits_L<overrightarrowdoverrightarrow>=5+6-10=1 left(Тлcdot мright).]

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09 02 2022