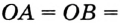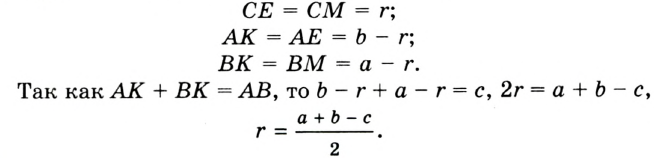554. Докажите, что если центр окружности, описанной около треугольника, принадлежит его высоте, то этот треугольник равнобедренный.
555. Докажите, что если центр окружности, вписанной в треугольник, принадлежит его медиане, то этот треугольник равнобедренный.
556. Докажите, что если центры вписанной и описанной окружностей треугольника совпадают, то этот треугольник равносторонний.
557. Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 7 : 5, считая от вершины треугольника. Найдите стороны треугольника, если его периметр равен 68 см.
558. Периметр треугольника ABC , описанного около окружности, равен 52 см. Точка касания со стороной AB делит эту сторону в отношении 2 : 3, считая от вершины A . Точка касания со стороной BC удалена от вершины C на 6 см. Найдите стороны треугольника.
559. В треугольник с углами 30°, 70° и 80° вписана окружность. Найдите углы треугольника, вершины которого являются точками касания вписанной окружности со сторонами данного треугольника.
560. Окружность, вписанная в равнобедренный треугольник ABC , касается его боковых сторон AB и BC в точках M и N соответственно. Докажите, что MN ‖ AC .
561. Докажите, что если центр окружности, описанной около треугольника, принадлежит его стороне, то этот треугольник — прямоугольный.

563. К окружности, вписанной в равносторонний треугольник со стороной a , провели касательную, пересекающую две его стороны. Найдите периметр треугольника, который эта касательная отсекает от данного.
564. В равнобедренный треугольник ABC ( AB = BC ) с основанием 10 см вписана окружность. К этой окружности проведены три касательные, отсекающие от данного треугольника треугольники ADK , BEF и CMN . Сумма периметров этих треугольников равна 42 см. Чему равна боковая сторона данного треугольника?
565. В треугольнике ABC отрезок BD — медиана, AB = 7 см, BC = 8 см. В треугольники ABD и BDC вписали окружности. Найдите расстояние между точками касания этих окружностей с отрезком BD .
566. Каждый из углов BAC и ACB треугольника ABC разделили на три равные части (рис. 308). Докажите, что ∠ AMN = ∠ CMN .
567. Пусть вершина угла B недоступна (рис. 309). С помощью транспортира и линейки без делений постройте прямую, содержащую биссектрису угла B .
568. Точки F и O — центры вписанной и описанной окружностей равнобедренного треугольника ABC соответственно (рис. 310). Они находятся на одинаковом расстоянии от его основания AC . Найдите углы треугольника ABC .
Упражнения для повторения
569. Биссектриса угла ABC образует с его стороной угол, равный углу, смежному с углом ABC . Найдите угол ABC .
570. В равнобедренном треугольнике из вершины одного угла при основании провели высоту треугольника, а из вершины другого угла при основании — биссектрису треугольника. Один из углов, образовавшихся при пересечении проведённых биссектрисы и высоты, равен 64°. Найдите углы данного треугольника.
571. На рисунке 311 BC ‖ AD , AB = 3 см, BC = 10 см. Биссектриса угла BAD пересекает отрезок BC в точке K . Найдите отрезки BK и KC .
572. В треугольнике ABC известно, что AB = BC , AM и CK — медианы этого треугольника. Докажите, что MK ‖ AC .
Наблюдайте, рисуйте, конструируйте, фантазируйте
573. В квадрате ABCD вырезали заштрихованную фигуру (рис. 312). Разделите оставшуюся часть квадрата на четыре равные фигуры.
- Описанные и вписанные окружности — формулы, свойства и определение с примерами решения
- Описанная и вписанная окружности треугольника
- Прямоугольный треугольник и его описанная и вписанная окружности
- Вписанные и описанные четырехугольники
- Окружность, вписанная в треугольник
- Описанная трапеция
- Дополнительные свойства и признаки вписанного четырехугольника
- Обобщенная теорема Пифагора
- Формула Эйлера для окружностей
- Справочная информация по описанной и вписанной окружности треугольника
- Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- 📹 Видео
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Описанные и вписанные окружности — формулы, свойства и определение с примерами решения
Содержание:
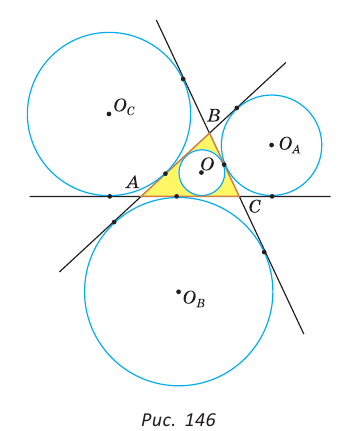
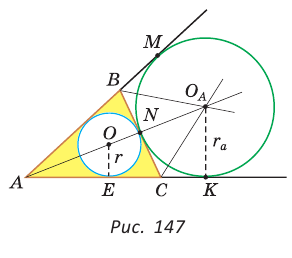
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника. На рисунке 146 изображен треугольник АВС и три его вневписанные окружности с центрами
Вневписанные окружности обладают рядом интересных свойств:
1. Центры вписанной и вневписанной окружностей лежат на биссектрисе соответствующего внутреннего угла треугольника.
2. 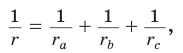
3. 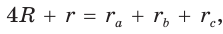
Попробуйте доказать некоторые из этих свойств.
Найдем радиус 
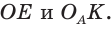
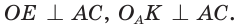
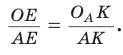
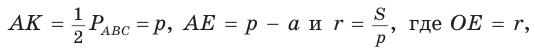
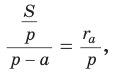
Пример:
Вычислим, используя данную формулу, радиус вневписанной окружности прямоугольного треугольника с катетами 3 и 4, которая касается гипотенузы:
Видео:Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

Описанная и вписанная окружности треугольника
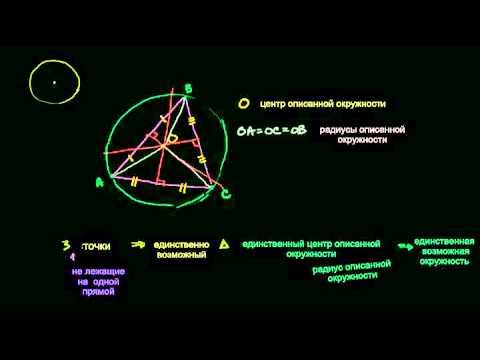
Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.
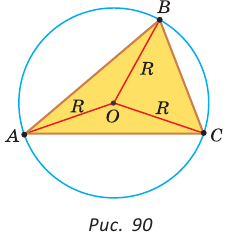
На рисунке 90 изображена окружность с радиусом R и центром 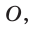
Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника.
Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС».
Теорема (об окружности, описанной около треугольника).
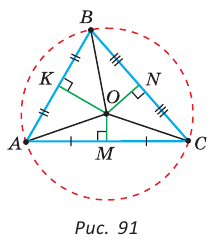
Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.
Рассмотрим произвольный треугольник АВС (рис. 91). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно.
Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них.
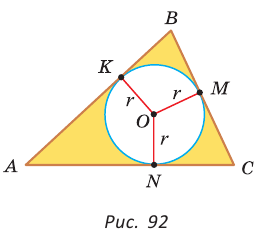
Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.
На рисунке 92 изображена окружность с центром О и радиусом 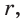
Так как 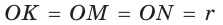
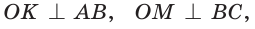
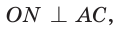
Вместо слов «окружность, вписанная в треугольник АВС», также говорят «вписанная окружность треугольника АВС».
Теорема (об окружности, вписанной в треугольник).
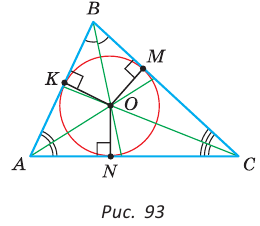
В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.
Рассмотрим произвольный треугольник АВС (рис. 93). Пусть О — точка пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОМ и ON соответственно к сторонам АВ, ВС и АС. По свойству биссектрисы угла ОК = ON, ON = ОМ. Окружность с центром в точке О и радиусом ОК будет проходить через точки К, М и N и касаться сторон АВ, ВС и АС в указанных точках по признаку касательной.
Следовательно, эта окружность является вписанной в треугольник АВС. Единственность вписанной окружности докажите самостоятельно.
Замечание. Так как все три биссектрисы треугольника пересекаются в одной точке, то для нахождения центра вписанной окружности достаточно построить точку пересечения любых двух из них.
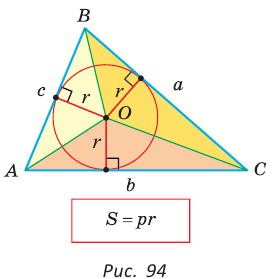
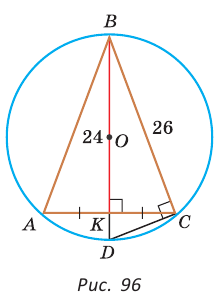
Теорема. Площадь треугольника можно найти по формуле 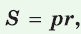
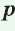
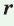
Пусть дан треугольник АВС со сторонами 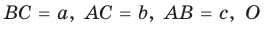
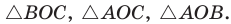
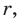
Следствие:
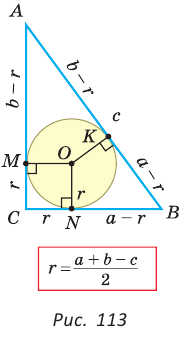
Радиус окружности, вписанной в треугольник, можно найти по формуле
Одной из важнейших задач данной темы является задача нахождения радиуса описанной и радиуса вписанной окружностей данного треугольника.
Пример:
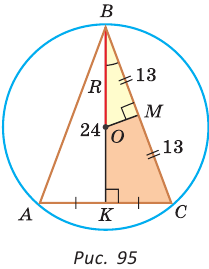
Найти радиус окружности, описанной около равнобедренного треугольника АВС, у которого АВ = ВС = 26 см, высота ВК = 24 см
(рис. 95).
Решение:
Способ 1 (метод подобия). Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Проведем серединные перпендикуляры к сторонам АС и ВС, которые пересекутся в точке О — центре описанной окружности. Так как в равнобедренном треугольнике высота, проведенная к основанию, является медианой, то ВК — серединный перпендикуляр к стороне АС. Пусть МО — серединный перпендикуляр к стороне ВС. Тогда ВМ = 13 см, ВО = R -— искомый радиус. Поскольку 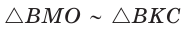
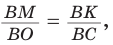
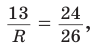
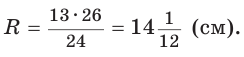
Способ 2 (тригонометрический метод). Из 
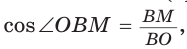
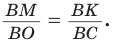
Способ 3* (среднее пропорциональное). Продлим высоту ВК до пересечения с описанной окружностью в точке D (рис. 96). Так как центр описанной окружности равнобедренного треугольника лежит на прямой ВК (см. способ 1), то BD = 2R — диаметр данной окружности. В прямоугольном треугольнике BCD 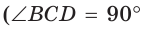
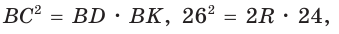
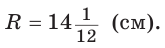
Ответ: 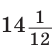
Замечание. Из решения ключевой задачи 1 следует свойство: «Центр окружности, описанной около равнобедренного треугольника, лежит на его высоте, проведенной к основанию, или на ее продолжении».
Верно и обратное утверждение: «Если центр окружности, описанной около треугольника, лежит на высоте треугольника или на ее продолжении, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Полезно запомнить!
Если в ключевой задаче 1 боковую сторону обозначить 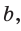
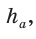
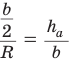
Отсюда следует удобная формула для нахождения радиуса окружности, описанной около равнобедренного треугольника:
Пример:
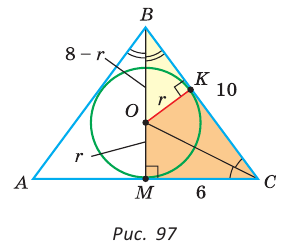
Найти радиус окружности, вписанной в равнобедренный треугольник АВС, у которого АВ = ВС = 10 см, АС = 12 см.
Решение:
Способ 1 (метод подобия). Центр вписанной окружности находится в точке пересечения биссектрис треугольника. Проведем в треугольнике АВС биссектрисы из вершин В и С, которые пересекутся в точке О — центре вписанной окружности (рис. 97). Биссектриса ВМ, проведенная к основанию равнобедренного треугольника АВС, будет его высотой и медианой, луч СО — биссектриса угла С, 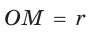
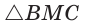
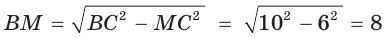
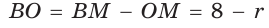
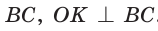
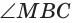
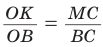
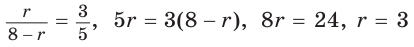
Способ 2 (тригонометрический метод). Из 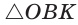
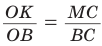
Способ 3 (свойство биссектрисы треугольника). СО — биссектриса 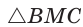
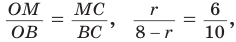
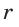
Способ 4 (формула 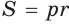
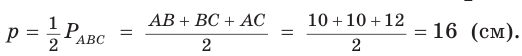
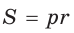
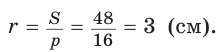
Ответ: 3 см.
Замечание. Из решения ключевой задачи 2 следует свойство: «Центр окружности, вписанной в равнобедренный треугольник, лежит на его высоте, проведенной к основанию».
Верно и обратное утверждение: «Если центр окружности, вписанной в треугольник, лежит на высоте треугольника, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Пример:
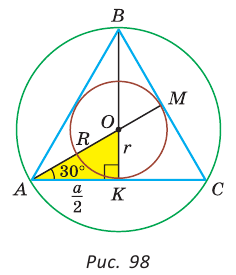
Дан равносторонний треугольник со стороной а. Найти радиус R его описанной окружности и радиус 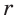
Решение:
Способ 1 (тригонометрический метод).Так как в равностороннем треугольнике биссектрисы являются и высотами, и медианами, то его биссектрисы лежат на серединных перпендикулярах к сторонам треугольника. Поэтому в равностороннем треугольнике центры описанной и вписанной окружностей совпадают.
Рассмотрим равносторонний треугольник АВС со стороной а, у которого высоты AM и ВК пересекаются в точке О — центре описанной и вписанной окружностей (рис. 98). Тогда ОА = OB = R — радиусы описанной, 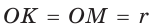
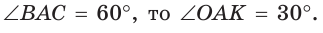
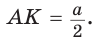
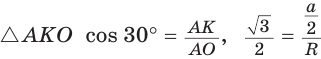
В 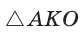
Способ 2 (свойство медиан). Поскольку AM и ВК — медианы треугольника АВС (см. рис. 98), то по свойству медиан 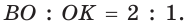
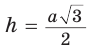
Ответ:
Полезно запомнить!
Поскольку радиус описанной окружности равностороннего треугольника 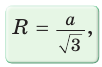
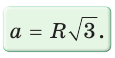
треугольника в 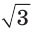
Чтобы найти радиус R описанной окружности равностороннего треугольника, нужно сторону 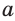
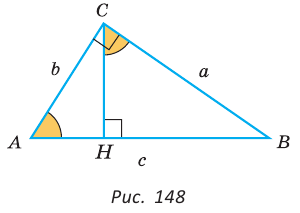
Прямоугольный треугольник и его описанная и вписанная окружности
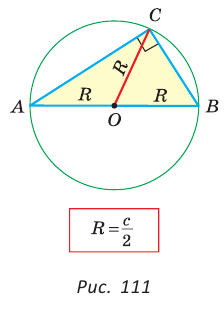
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а ее радиус равен половине гипотенузы, т. е. 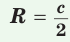
Проведем в прямоугольном треугольнике АВС медиану СО к гипотенузе АВ (рис. 111). Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы, то ОС = ОА = ОВ.
Тогда середина гипотенузы — точка О — равноудалена от точек А, В и С и поэтому является центром описанной окружности треугольника АВС. Радиус этой окружности 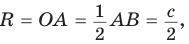
Теорема доказана.
Замечание. Также можно доказать, что серединные перпендикуляры к катетам прямоугольного треугольника пересекаются на середине гипотенузы.
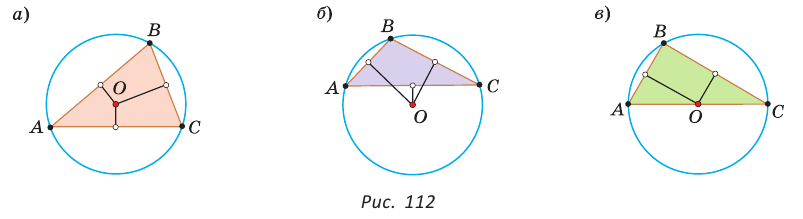
Отметим, что у остроугольного треугольника центр описанной окружности лежит внутри треугольника (рис. 112, а), у тупоугольного — вне треугольника (рис. 112, б), у прямоугольного — на середине гипотенузы (рис. 112, в). Обоснуйте первые два утверждения самостоятельно.
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле 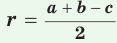
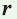
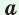
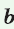
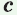
Рассмотрим прямоугольный треугольник АВС с катетами 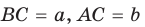
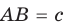
Проведем радиусы в точки касания и получим: 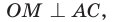
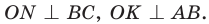
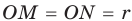
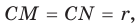
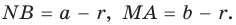
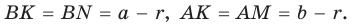
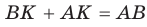
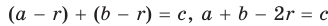
Следствие: 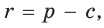
Преобразуем формулу радиуса вписанной окружности:
Формула 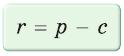
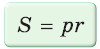
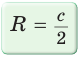
Пример. Дан прямоугольный треугольник, 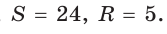
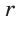
Решение:
Так как 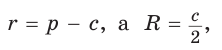
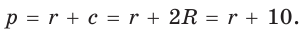
Из формулы 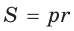
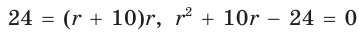
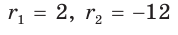
Ответ: 
Пример:
Найти радиус окружности, описанной около прямоугольного треугольника, у которого один из катетов равен 6, а радиус вписанной окружности равен 2.
Решение:
Способ 1 (геометрический). Пусть в треугольнике АВС, где 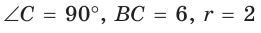
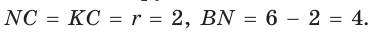
По свойству касательных 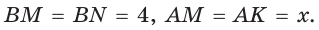
Тогда 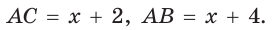
Следовательно, 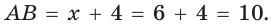
Радиус описанной окружности 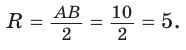
Способ 2 (алгебраический). Подставив в формулу 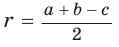
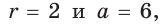
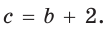
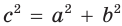
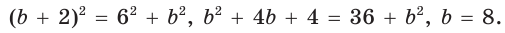
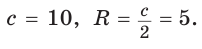
Ответ: 5.
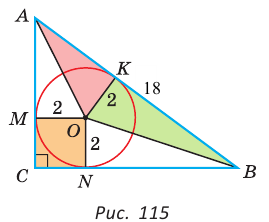
Пример:
Гипотенуза прямоугольного треугольника 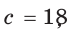
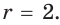
Решение:
Способ 1 (геометрический). Пусть в 
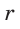
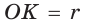
Отсюда 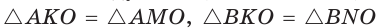
Площадь 
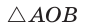
Способ 2 (алгебраический). Из формулы 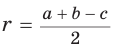
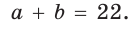
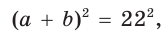
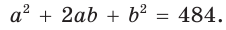
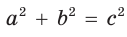
Способ 3 (алгебраический). Из формулы 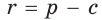
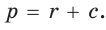
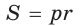
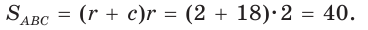
Ответ: 40.
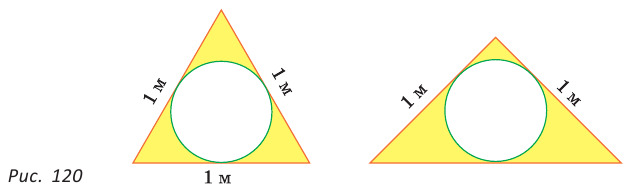
Реальная геометрия:
Есть два листа ДСП (древесно-стружечной плиты). Один из них имеет форму равностороннего треугольника со стороной 1 м, другой — форму прямоугольного равнобедренного треугольника с катетами, равными 1 м (рис. 120). Из каждого листа необходимо вырезать по одному кругу наибольшего диаметра. Определите, из какого листа будет вырезан круг большего диаметра и каким в этом случае будет процент отходов, если известно, что площадь круга можно найти по формуле
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанные и описанные четырехугольники
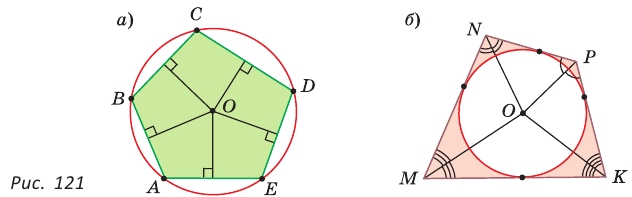
Определение. Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность.
Окружность называется вписанной в многоугольник, если она касается всех его сторон. При этом много угольник называется описанным около окружности.
Пятиугольник ABCDE (рис. 121, а) является вписанным в окружность а четырехугольник MNPK (рис. 121, б) — описанным около окружности.
Центр описанной окружности многоугольника находится в точке пересечения серединных перпендикуляров к его сторонам, а центр вписанной — в точке пересечения биссектрис его углов.
Обоснуйте эти утверждения самостоятельно.
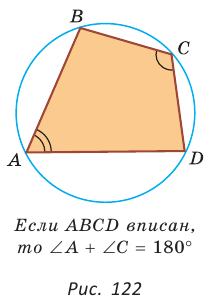
Теорема (свойство вписанного четырехугольника).
Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°.
Пусть ABCD — четырехугольник, вписанный в окружность (рис. 122). Его углы А, В, С и D являются вписанными в окружность. Так как вписанный угол равен половине дуги, на которую он опирается, то 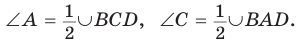
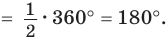
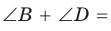
Теорема (признак вписанного четырехугольника).
Если сумма противоположных углов четырехугольника равна 
Рассмотрим четырехугольник ABCD, у которого 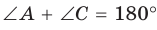
Тогда сумма 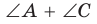
Замечание. Так как сумма углов четырехугольника равна 360°, то для того чтобы около четырехугольника можно было описать окружность, достаточно, чтобы сумма любой пары его противоположных углов была равна 180°.
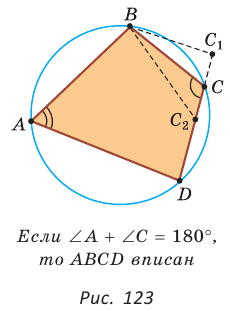
Следствия.
1. Около параллелограмма можно описать окружность, только если этот параллелограмм — прямоугольник (рис. 124, а). Центр этой окружности лежит в точке пересечения диагоналей прямоугольника.
2. Около ромба можно описать окружность, только если этот ромб — квадрат (рис. 124, б).
3. Около трапеции можно описать окружность, только если она равнобедренная (рис. 124, в).
Докажите эти следствия самостоятельно.
Теорема (свойство описанного четырехугольника ).
Суммы противоположных сторон описанного четырехугольника равны между собой.
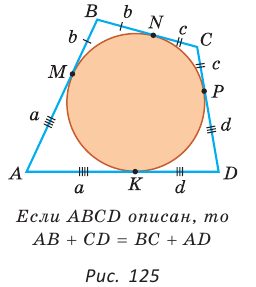
Пусть ABCD — описанный четырехугольник, М, N, Р и К — точки касания его сторон с окружностью (рис. 125). Так как отрезки касательных, проведенных к окружности из одной точки, равны между собой, то AM = АК = а, ВМ = BN = b, СР = CN = с, DP = DK = d. Тогда
откуда AD + ВС = AB + CD.
Теорема доказана.
Следствие:
Периметр описанного четырехугольника равен удвоенной сумме длин любой пары его противоположных сторон:
Теорема (признак описанного четырехугольника).
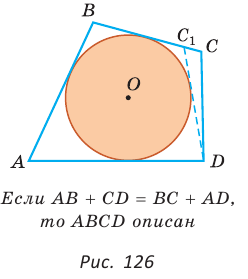
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Пусть для выпуклого четырехугольника ABCD справедливо, что
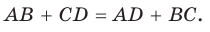
Проведем окружность, которая касается прямых AD, АВ и ВС (рис. 126). Такая окружность существует, ее центр находится в точке пересечения биссектрис углов А и В. Если окружность не касается стороны CD, то либо прямая CD не имеет с окружностью общих точек, либо является секущей. Рассмотрим первый случай. Проведем отрезок 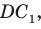
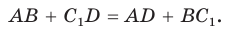
Отняв почленно от равенства (1) равенство (2), получим 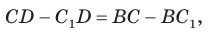
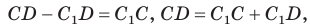
Рассмотрев случай, когда прямая DC — секущая, также придем к противоречию (сделайте это самостоятельно). Следовательно, данная окружность касается стороны CD и в четырехугольник ABCD можно вписать окружность. Теорема доказана.
Следствия.
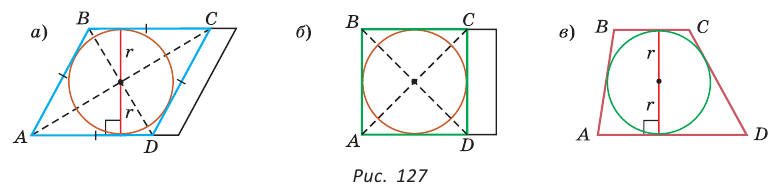
1. В параллелограмм можно вписать окружность, только если этот параллелограмм — ромб. Центр этой окружности лежит в точке пересечения диагоналей ромба, а ее диаметр равен высоте ромба (рис. 127, а).
2. В прямоугольник можно вписать окружность, только если этот прямоугольник — квадрат (рис. 127, б).
3. Диаметр окружности, вписанной в трапецию, равен ее высоте (рис. 127, в).
Докажите эти следствия самостоятельно.
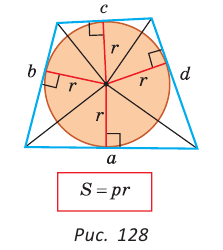
Для описанного многоугольника справедлива формула 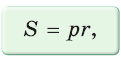
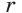
Доказательство аналогично приведенному в § 8 для треугольника. Выполните его самостоятельно, используя рисунок 128.
Пример:
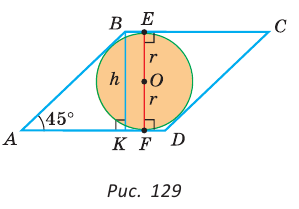
Найти радиус окружности, вписанной в ромб с периметром 24 см и острым углом, равным 45°.
Решение:
Способ 1 (решение прямоугольного треугольника). Пусть ABCD — ромб (рис. 129), О — центр вписанной в ромб окружности. Известно, что высота ВК ромба равна диаметру EF вписанной окружности, т. е. 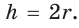
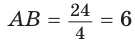
Из прямоугольного треугольника АВК находим. что 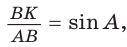
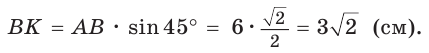
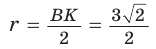
Способ 2 (метод площадей). Ромб — параллелограмм. По формуле площади параллелограмма 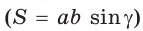
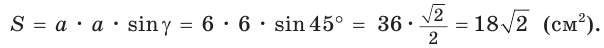
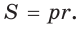
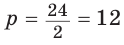
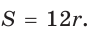
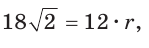
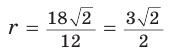
Ответ: 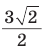
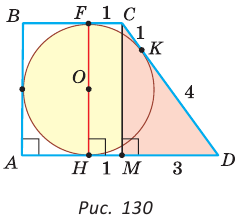
Пример:
Окружность, вписанная в прямоугольную трапецию ABCD, где 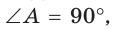
Решение:
Способ 1. Площадь трапеции находится по формуле 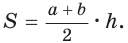
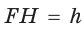
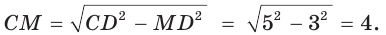
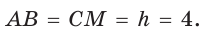
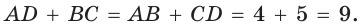
Способ 2*. Центр О вписанной окружности лежит на пересечении биссектрис углов 
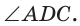
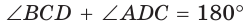
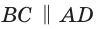
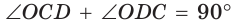
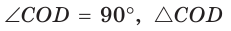
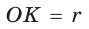
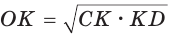
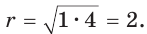
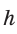
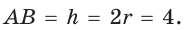
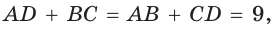
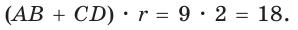
Ответ: 18.
Замечание. Полезно запомнить свойство: «Боковая сторона описанной трапеции видна из центра вписанной окружности под углом 90°».
Пример:
Внутри острого угла А взята точка М, из которой опущены перпендикуляры МВ и МС на стороны угла А, 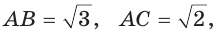
Решение:
Так как в четырехугольнике АВМС сумма углов В и С равна 180°, то около него можно описать окружность. Проведем в ней хорду AM (рис. 132, б). Поскольку 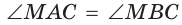
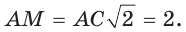
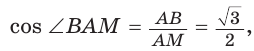
Окружность, вписанная в треугольник
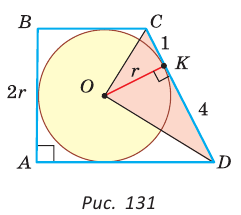
Пример:
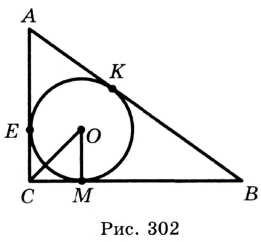
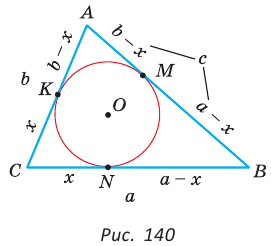
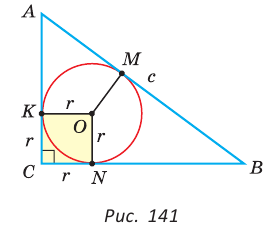
Окружность вписана в треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с. Вывести формулу для нахождения длин отрезков, на которые точки касания окружности со сторонами делят каждую сторону треугольника.
Решение:
Пусть К, М и N — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника АВС (рис. 140). Известно, что отрезки касательных, проведенных из одной точки к окружности, равны между собой.
Тогда, если 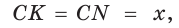
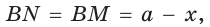
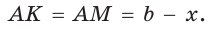
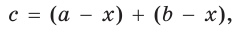
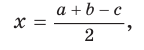
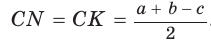
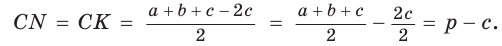
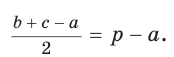
Ответ:
Замечание. Если 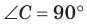
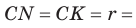
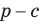
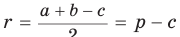
Описанная трапеция
Пример:
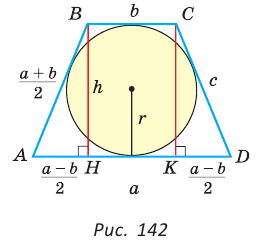
Найти площадь описанной равнобедренной трапеции с основаниями а и Ь.
Решение:
Площадь трапеции можно найти по формуле 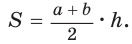
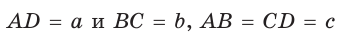
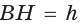
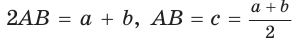
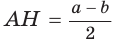
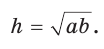
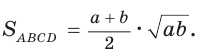
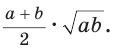
Замечание. Площадь описанной равнобедренной трапеции равна произведению среднего арифметического и среднего геометрического ее оснований.
Полезно запомнить!
Для описанной равнобедренной трапеции с основаниями 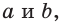
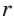
Дополнительные свойства и признаки вписанного четырехугольника
Теорема.
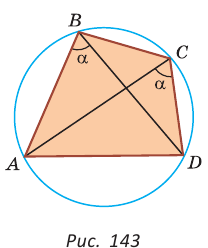
Около четырехугольника можно описать окружность тогда и только тогда, когда угол между его стороной и диагональю равен углу между противоположной стороной и другой диагональю.
Рис. 143
1. Если четырехугольник ABCD вписан в окружность (рис. 143), то 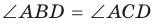
2. Докажем, что если в некотором четырехугольнике ABCD 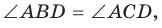
Опишем около треугольника ABD окружность.
В 8-м классе (В. В. Казаков. «Геометрия, 8», с. 186) было доказано свойство:
«Геометрическим местом точек плоскости, из которых данный отрезок AD виден под углом а, является объединение двух дуг окружностей: дуги ABD и ей симметричной относительно прямой AD, исключая точки 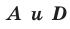
Обобщенная теорема Пифагора
В прямоугольном треугольнике 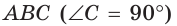
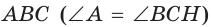
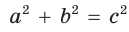
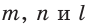
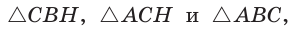
Действительно, из подобия указанных треугольников 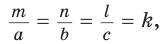
Пример:
Пусть 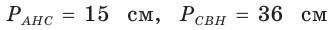
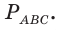
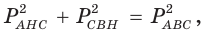
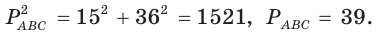
Ответ: 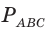
Формула Эйлера для окружностей
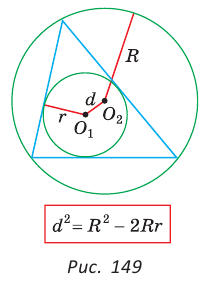
Для вписанной и описанной окружностей треугольника с радиусами 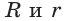
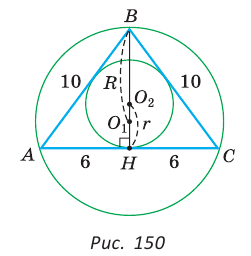
Проверим справедливость этой формулы на примере равнобедренного треугольника АВС, у которого АВ = ВС = 10, АС = 12 (рис. 150).
Вначале найдем расстояние между центрами указанных окружностей традиционным способом.
Проведем высоту ВН, длина которой будет равна 8 (пифагорова тройка 6, 8, 10). Центры описанной и вписанной окружностей — соответственно точки 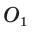
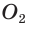
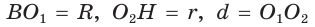
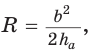
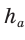
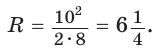
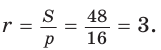
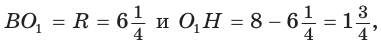
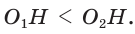
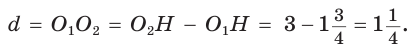
А теперь найдем d по формуле Эйлера:
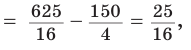
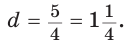
Запомнить:
- Центр описанной окружности треугольника (многоугольника) лежит в точке пересечения серединных перпендикуляров к его сторонам.
- Центр вписанной окружности треугольника (многоугольника) лежит в точке пересечения биссектрис его углов.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, а ее радиус равен половине гипотенузы:
- Радиус вписанной окружности прямоугольного треугольника находится по формуле
- Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°. И обратно.
- Если четырехугольник описан около окружности, то суммы его противоположных сторон равны между собой. И обратно.
- Площадь треугольника и описанного многоугольника можно найти по формуле
где
— полупериметр,
— радиус вписанной окружности.
Справочная информация по описанной и вписанной окружности треугольника
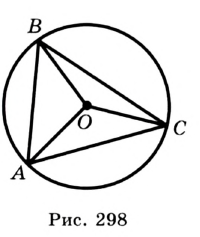
Определение. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.
На рисунке 298 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность. Очевидно, что центр описанной окружности треугольника равноудален от всех его вершин. На рисунке 298 точка 
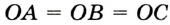
Теорема 21.1. Вокруг любого треугольника можно описать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 
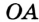
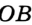
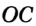
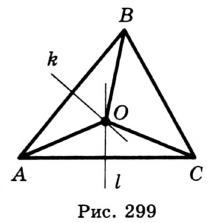
На рисунке 299 изображен произвольный треугольник 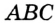
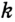
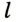
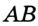
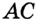
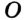

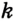
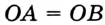
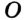
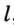
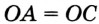
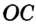

Заметим, что вокруг треугольника можно описать только одну окружность. Это следует из того, что серединные перпендикуляры 
Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Следствие 2. Центр описанной окружности треугольника — это точка пересечения серединных перпендикуляров его сторон.
Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон.
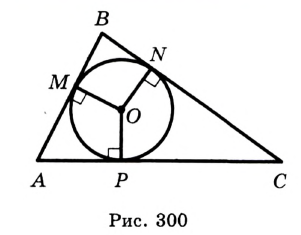
На рисунке 300 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
Точка 
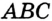
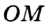
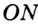
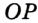
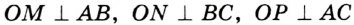
Теорема 21.2. В любой треугольник можно вписать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 
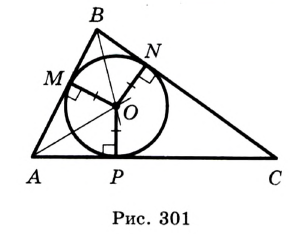
На рисунке 301 изображен произвольный треугольник 




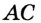


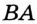
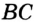

Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов 

Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке.
Следствие 2. Центр вписанной окружности треугольника — это точка пересечения его биссектрис.
Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле 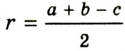
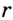
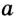
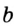
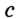
Решение:
В треугольнике 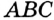
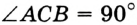
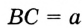
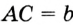
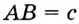
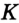
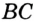
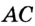
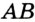
Отрезок 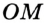
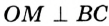
Так как точка 
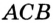
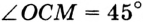
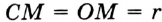
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Первый признак равенства треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Описанная и вписанная окружности треугольникаСкачать

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
 Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Окружность и треугольникСкачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||
| Произвольный треугольник | ||
 | ||
| Равнобедренный треугольник | ||
 | ||
| Равносторонний треугольник | ||
 | ||
| Прямоугольный треугольник | ||
 | ||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
📹 Видео
Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Геометрия Четырехугольник оказался вписанным Задача №26 ОГЭСкачать

Три точки, задающие окружностьСкачать
Описанная и вписанная окружности треугольникаСкачать

Геометрия Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершинСкачать

Тема 7. Вписанные и описанные окружности треугольникаСкачать

Вторая замечательная точка треугольникаСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Описанная окружность 1. Центр окружности, описанной около треугольника.Скачать

Радиус описанной окружностиСкачать

7 класс | УРОК №4 | Геометрия. Описанная и вписанная окружности треугольника.Скачать

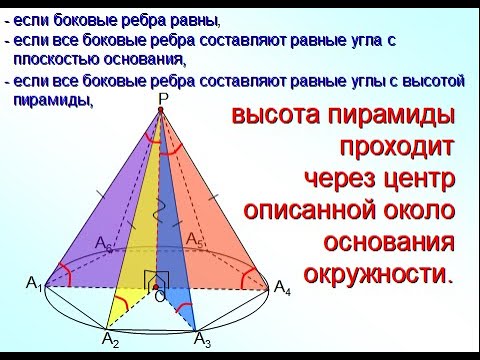
Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать











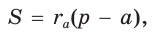
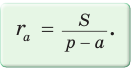
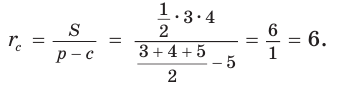
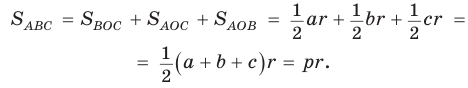
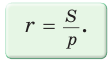
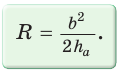
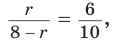
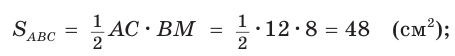
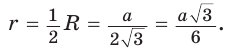
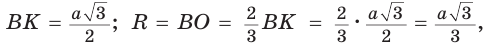
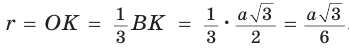
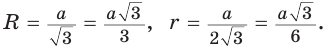
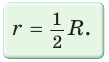
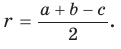
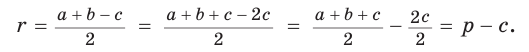
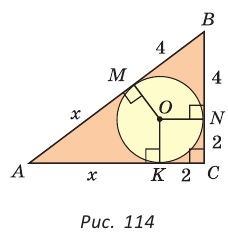
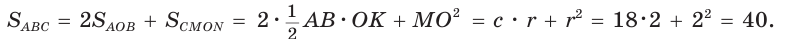
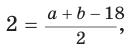
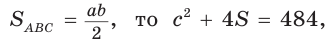
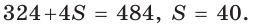
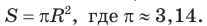

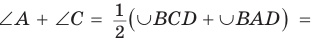
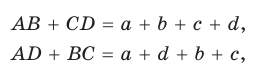
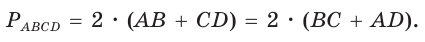
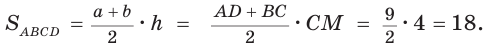
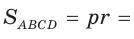
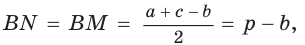
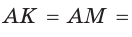
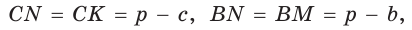
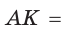
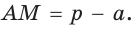
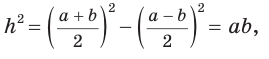
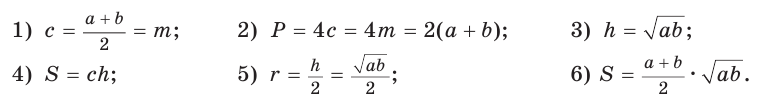
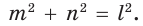
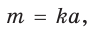
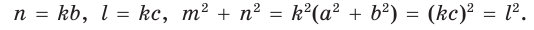
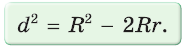
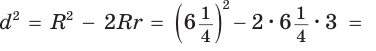
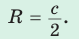
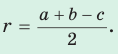
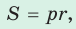 где
где 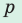 — полупериметр,
— полупериметр, 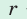 — радиус вписанной окружности.
— радиус вписанной окружности.