Центр масс колеса движется по окружности (5 видео)

Центр масс колеса движется по окружности

Глава 14. Теоремы о движении центра масс и об изменении количества движения и кинетического момента.

14.1. Теорема о движении центра масс.

14.1.1. Положение центра масс С механической системы массой m = 50 кг определяется радиусом-вектором r_с = 3i + 4j + 5k. Опрeделить статический момент масс этой системы относительно плоскости Оху. (Ответ 250)

14.1.2. Определить координату хс центра масс кривошипно-ползунного механизма при углах φ = 90 о и α = 30°, если масса кривошипа 1 равна 4 кг, а масса шатуна 2 равна 8 кг. Шатун 2 длиной 0,8 м считать однородным стержнем. Массой ползуна 3 пренебречь. (Ответ 0,231)

14.1.3. Тело массой m = 2 кг движется по горизонтальным направляющим согласно закону s = 2t 2 + 1. Определить модуль главного вектора внешних сил, действующих на тело. (Ответ 8)

14.1.4. Тело 1 массой m = 50 кг поднимается по наклонной плоскости с помощью троса, наматываемого на барабан 2 радиуса R = 0,4 м. Определить модуль главного вектора внешних сил, действующих на тело 1, если угловое ускорение барабана ϵ = 5 рад/с 2 . (Ответ 100)

14.1.5. Механическая система движется так, что проекции ускорения ее центра масс С на оси координат равны а_Сх = 1 м/с 2 , а_Су = 2 м/с 2 , a_Cz = 4 м/с 2 . Определить модуль главного вектора внешних сил, действующих на систему, если масса системы m = 40 кг. (Ответ 183)

14.1.6. Движение центра масс механической системы определяется радиусом-вектором r_с = 2 cos πti + 2 sin πtj. Определить проекцию на ось Оу главного вектора внешних сил в момент времени t = 0,5 с, если масса системы m = 10 кг. (Ответ -197)

14.1.7. Диск массой m = 20 м вращается равномерно вокруг неподвижной оси с угловой скоростью ω = 10 рад/с. Определить модуль главного вектора внешних сил, приложенных к диску, если его центр тяжести удален от оси вращения на расстояние ОС = 0,5 см. (Ответ 10)

14.1.8. Центр масс колеса С движется по окружности радиуса R = 1,3 м согласно закону s = 4t. Определить модуль главного вектора внешних сил, приложенных к колесу, если его масса m = 15 кг. (Ответ 185)

14.1.9. Кривошип 1 шарнирного параллелограмма вращается равномерно с угловой скоростью ω₁ = 5 рад/с. Определить модуль главного вектора внешних сил, действующих на звено 2, если его масса m = 8 кг, длина ОА = 0,4 м. (Ответ 80)

14.1.10. Однородный равносторонний треугольник ОАВ массой m = 5 кг вращается равномерно вокруг неподвижной оси. Определить его угловую скорость ω, если главный вектор внешних сил, действующих на него, равен 300Н, а длина l = 0,4 м. (Ответ 16,1)

14.1.11. Шкив 2 радиуса R = 0,2 м, вращаясь с угловым ускорением ϵ₂ = 10 рад/с 2 , поднимает однородный цилиндр 1, масса которою m = 50 кг. Определить модуль главного вектора внешних сил, действующих на цилиндр. (Ответ 50)

14.1.12. Однородный диск радиуса R = 0,5 м, масса которого m = 20 кг, вращается с постоянным угловым ускорением ϵ = 10 рад/с 2 . Определить модуль главного вектора внешних сил, действующих на диск. (Ответ 0)

14.1.13. Однородный стержень ОА массой m = 10 кг вращается равномерно с угловой скоростью ω = 10 рад/с. Определить модуль главного вектора внешних сил, действующих на стержень, если его длина ОА = 1 м. (Ответ 500)

14.1.14. Ползун А движется под действием силы F с постоянной скоростью v_A. Определить реакцию направляющей на ползун А в тот момент времени, когда ускорение ползуна В равно а_в = 4 м/с 2 , если масса однородного стержня АВ равна 5 кг. Массой ползунов пренебречь.
(Ответ 10)

14.1.15. Кривошип 1 длиной ОА = 0,25 м, вращаясь равномерно с угловой скоростью ω = 10 рад/с, приводит в движение кулису 2, масса которой m = 5 кг. Определить модуль главного вектора внешних сил, действующих на кулису в момент времени, когда угол φ = 60°.
(Ответ 62,5)

14.1.16. Определить модуль главного вектора внешних сил, действующих на шатун АВ кривошипно-ползунного механизма в момент времени, когда угол φ = 180°, а точки А и В имеют ускорения а_А = 10 м/с 2 , а_в = 14 м/с 2 . Шaтун массой m = 5 кг считать однородным стержнем. (Ответ 60)

14.1.17. Определить проекцию ускорения центра масс С механической системы на ось О_у в момент времени, когда координата у_С = 0.8 м, если масса системы m = 10 кг, а главный вектор приложенных внешних сил R e = 3i + 6tj. В начальный момент времени центр масс системы находился в точке О в покое. (Ответ 1,2)

14.1.18. Тело 1 массой 4 кг может двигаться по горизонтальной направляющей. На какое расстояние переместится тело 1, когда однородный стержень 2 массой 2 кг и длиной l = 0,6 м. опускаясь под действием силы тяжести, займет вертикальное положение. В начальный момент система находилась в покое. (Ответ 0,1)

14.1.19. Тело 1 массой m₁ = 0,7 кг может двигаться по горизонтальной направляющей. Определить модуль ускорения тела 1 в момент времени t = 0,25 с, если относительно него под действием внутренних сил системы движется тело 2 массой m₂ = 0,1 кг согласно уравнению s = sin 4t. (Ответ 0,841)

14.1.20. На тело 1 действует постоянная сила F = 10Н. Определить ускорение этого тела в момент времени t = 0,5 с, если относительно него под действием внутренних сил системы движется тело 2 согласно уравнению x = cos πt. Массы тел: m₁ = 4 кг, m₂ = 1 кг. Тела движутся поступательно. (Ответ 2)

14.1.21. Определить ускорение тела 1, скользящего но гладкой наклонной плоскости, если в горизонтальных направляющих относительно него под действием внутренних сил системы движется тело 2 согласно уравнению x = t 2 . Массы тел: m₁ = m₂ = 1 кг. Тела движутся поступательно. (Ответ 4,04)

Видео:Центр массСкачать

Тема 10. Теорема о движении центра масс. Количество движения и кинетический момент механической системы. Теорема об изменении количества движения. Теорема об изменении кинетического момента.

I: 213.

S:Человек массы m = 60 кг переходит с носа на корму лодки. На какое расстояние по величине | s |переместится лодка длины l = 3 м, если её масса M = 120 кг?

I: 214.

S:Колесо радиуса R = 0,5 м и массы m = 10 кг катится со скольжением по горизонтальной прямой под действием приложенного к нему вращательного момента M = 6 Нּм. Определить ускорение a_C центра масс C колеса, если коэффициент трения скольжения равен f = 0,1. Ускорение свободного падения принять равным g = 10 м/с 2 . a_C = …

I: 215.

S:Колесо радиуса R = 0,5 м и массы m = 10 кг скатывается с наклонной плоскости вниз. Его центр масс C движется по закону x_C = t 2 (м). Определить модуль главного вектора внешних сил |F ( e ) |, действующих на колесо; |F ( e ) | = … (Н).

I: 216.

S:Тело массы m = 40 г, брошенное вертикально вверх с начальной скоростью v₀ = 30 м/с, достигло высшей тоски спустя время t = 2,5 сек. Найти среднюю силу сопротивления F _сопр. воздуха, действовавшую на тело во время движения. (Результат вычисления округлить до третьего знака после запятой включительно.) (g = 9,81 м/с 2 ) F _сопр. = … (Н)

I: 217.

S:Тело 1 массой m = 50 кг поднимается по наклонной плоскости с помощью троса, намотанного на барабан 2 радиуса R = 0,4 м. Угловое ускорение барабана ε = 5 рад/с 2 . Определить модуль вектора всех внешних сил вектора внешних сил |F ( e ) |, действующих на тело;

I: 218.

S:Шкив 1 массы М = 20 кг и радиуса R = 0,4 м, вращаясь с угловой скоростью ω = 2,5 рад/с, поднимает груз 2 массы m = 10 кг. Определить модуль количества движения |Q| механизма;

I: 219.

S:Мяч массы m = 150 г ударяется о гладкую стенку под углом α = 30 о к ней и отскакивает без потери скорости. Найти среднюю силу F, действующую на мяч со стороны стенки, если скорость мяча v₀ = 10 м/с, а продолжительность удара Δ t = 0,1 сек. F = … (Н).

I: 220.

S:Масса каждого из тёх звеньев шарнирного параллелограмма ОАВС (ОА, АВ, СВ)равна 3 кг. Длина кривошипа ОА равна 0,6 м. Кривошип ОА вращается равномерно с угловой скоростью ω = 5 рад/с.

Определить модуль количества движения |Q| механизма; |Q| = … (кгּм/с).

I: 221.

S:Поезд массы m = 500 тонн после прекращения тяги тепловоза останавливается под действием силы трения F_тр = 0,1 МН (мега-ньютон) через время t = 1 мин. С какой скоростью v шёл поезд до момента прекращения тяги тепловоза? v = …(м/с)

I: 222.

S:Цилиндр 1 вращается с угловой скоростью ω = 20 рад/с. Его момент инерции относительно оси вращения Ј = 2 кгּм 2 , радиус r = 0,5 м. Груз 2 имеет массу m₂ = 1 кг.

Определить модуль количества движения |Q| механизма; |Q| = … (кгּм/с).

I: 223.

S:В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 3 кг, а ползун В имеет массу m/2 = 1,5 кг. Длина кривошипа OA l = 0,6 м, длина шатуна AB 2ּl = 1,2 м. Угловая скорость кривошипа равна ω= 5 рад/с.

Определить модуль количества движения |Q| механизма в тот момент, когда угол α = π/2;

I: 224.

S:Какова средняя сила давления F на плечо при стрельбе из автомата, если масса пули m = 10 г, а скорость пули при вылете из ствола v = 300 м/с? Число выстрелов из автомата в единицу времени n = 300 мин – 1 . F = … (Н).

I: 225.

S:Орудие, имеющее массу ствола М = 500 кг, стреляет в горизонтальном направлении. Масса снаряда m = 5 кг, его начальная скорость v = 460 м/с. При выстреле ствол откатывается на расстояние s = 40 см. Найти среднюю силу торможения F(кН), возникающую в механизме, тормозящем ствол (результат вычисления округлить до целого числа); F = … (килоньютон)

I: 226.

S:Человек, стоящий на коньках на гладком льду реки, бросает камень массы m = 0,5 кг. Спустя время t = 2 сек. камень достигает берега, пройдя расстояние s = 20 м. С какой скоростью u начинает скользить конькобежец, если его масса M = 60 кг? Трением пренебречь. (Результат вычисления округлить до второго знака после запятой включительно.)

I: 227.

S:Тело массы M = 990 г лежит на горизонтальной поверхности. В него попадает пуля массы m = 10 г и застревает в нём. Скорость пули v = 700 м/с и направлена горизонтально. Какой путь s пройдет тело до остановки? Коэффициент трения между телом и поверхностью k = 0,05. (Результат вычисления округлить до целого числа.) (g = 9,8 м/с 2 )

I: 228.

S:Ракета, имеющая вместе с зарядом массу M = 250 г, взлетает вертикально вверх и достигает высоты h = 150 м. Масса заряда m = 50 г. Найти скорость v истечения газовиз ракеты (относительно земли), считая, что сгорание заряда происходит мгновенно. (Результат вычисления округлить до целого числа.)

I: 229.

S:Масса платформы с орудием и боеприпасами составляет M = 20 тонн. С этой платформы, движущейся со скоростью u = 9 км/час, производится выстрел из орудия. Снаряд массы m = 25 кг вылетает из ствола орудия со скоростью v = 700 м/с (относительно орудия). Найти скорость платформы u₁ (км/час) непосредственно после выстрела, если направления движения платформы и выстрела совпадают. (Результат вычисления округлить до целого числа.)

I: 230.

S:Масса платформы с орудием и боеприпасами составляет M = 20 тонн. С этой платформы, движущейся со скоростью u = 9 км/час, производится выстрел из орудия. Снаряд массы m = 25 кг вылетает из ствола орудия со скоростью v = 700 м/с (относительно орудия). Найти скорость платформы u₁ (км/час) непосредственно после выстрела, если направления движения платформы и выстрела противоположны. (Результат вычисления округлить до целого числа.)

I: 231

S:Ядро, летевшее со скоростью v = 200 м/с, разорвалось на два осколка с массами m₁ = 10 кг и m₂ = 5 кг. Скорость первого осколка v₁ = 300 м/с и направлена так же, как и скорость ядра до разрыва. Найти скорость v₂ второго (меньшего) осколка; v₂ = … (м/с).

I: 232.

S:Центр масс колеса С движется по окружности радиуса R = 1,6 м согласно закону s = 4ּt (м). Масса колеса m = 15 кг.

Модуль главного вектора внешних сил, приложенных к колесу равен … (Н)

I: 233.

S:Трубка вращается вокруг вертикальной оси Oz, её момент инерции Ј_z = 0,075 кгּм 2 . По трубке под действием внутренних сил системы движется шарик М массой m = 0,1 кг. Когда шарик находится на Оz, угловая скорость ω₀ = 4 рад/с. Затем угловая скорость становится равной ω₁ = 3 рад/с. Это стало на расстоянии l.

Определить расстояние l; l = … (м).

I: 234.

S:Тело вращается вокруг вертикальной оси Oz под действием пары сил с моментом М = 16ּt (Нּм). При t = 0 тело находилось в покое, а в момент t = 3 с угловая скорость ω = 2 рад/с.

Определить момент инерции (кгּм 2 ) тела относительно оси Oz.

Отметьте правильный ответ.

I: 235.

S:Горизонтальная трубка CD может свободно вращаться вокруг вертикальной оси AB. Внутри трубки на расстоянии b = 0,2 м, от оси находится шарик M. В некоторый момент времени трубке сообщается начальная угловая скорость ω₀ = 5 рад/сек. Определить угловую скорость ω трубки в момент, когда шарик вылетит из трубки. Момент инерции трубки относительно оси вращения равен J = 0,7 кгּм 2 , её длина L = 1 м; шарик считать материальной точкой массы m = 0,5 кг; трением пренебречь. ω = … (рад/с).

I: 236.

S:Два вагонамасс m₁ = 20 тонн и m₂ = 30 тонн, двигавшиеся навстречу друг другу по горизонтальному прямолинейному участку пути со скоростями v₁ = 3 м/с и v₂ = 2,5 м/с соответственно, сцепляются после соударения. Пренебрегая сопротивлениями движению, определить модуль скорости v сцепа; v = … (м/с).

I: 247.

S:Снаряд массы m = 12 кг, летевший со скоростью v = 800 м/с, разорвался в воздухе на 240 равных по массе осколков. Разлёт осколков в системе отсчёта, связанной с первоначальным снарядом, является сферически симметричным, и скорость каждого осколка в этой системе отсчёта равна v_отн = 600 м/с. Модуль количества движения системы осколков относительно земли равен … (кгּм/с).

I: 238.

S:Кривошипно-ползунный механизм прикреплён к станине массы M, установленной на гладком горизонтальном фундаменте. Масса ползуна B механизма равна m, причём M = 9ּm. Пренебрегая массой звеньев OA и AB, длины которых соответственно OA = l, OA и AB = 2ּl, найти максимальное значение v_max скорости станины, если кривошип вращается с постоянной угловой скоростью ω и при t = 0 угол φ = 0 и начальная скорость станины равна нулю.

Искомая скорость v_max имеет вид v_max = Κּωּl. Определить Κ (результат вычисления – с точностью до первого знака после запятой). Κ = … .

I: 239.

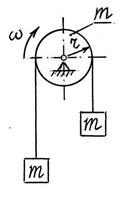
S:Через участки трубы постоянного сечения и различной формы со скоростью v протекает жидкость заполняющая всё сечение трубы. Направление установившегося движения жидкости указано на рисунке стрелками. Полагая вес участков трубы и заполняющей их жидкости одинаковыми во всех четырёх случаях, установить, в каком из этих случаев сила нормального давления трубы на основание оказывается наибольшей

I: 240.

S:Шарик массой m = 100 г свободно упал на горизонтальную площадку, имея в момент удара скорость v = 10 м/с. Найти модуль изменения количества движения при абсолютно неупругом |Q_{неупруг}| и абсолютно упругом |Q_упруг| ударах;

I: 241.

S:Диск массой m = 20 кг вращается равномерно вокруг неподвижной оси с угловой скоростью ω = 10 рад/с. Центр тяжести удалён от оси вращения на расстояние ОС = 0,5 см.

Модуль главного вектора внешних сил, приложенных к диску, равен … (Н).

I: 242.

S:Два груза одинаковой массы m = 2 кг каждый закреплены по концам невесомого нерастяжимого каната, переброшенного через однородный шкив массы m = 2 кг и радиуса r = 0,1 м. Зная угловую скорость вращения ω = 5 рад/с шкива и пренебрегая проскальзыванием каната относительно шкива, определить модуль количества движения |Q| данной механической системы; |Q| = … (кгּм/с).

I: 243.

S:Два груза одинаковой массы m = 2 кг каждый закреплены по концам невесомого нерастяжимого каната, переброшенного через однородный шкив массы m = 2 кг и радиуса r = 0,1 м. Зная угловую скорость вращения ω = 5 рад/с шкива и пренебрегая проскальзыванием каната относительно шкива, определить модуль кинетического момента |K_z| данной механической системы относительно оси вращения (числовой результат определить с точностью до второго знака после запятой);

I: 244.

S: Материальная точка массой 1 кг равномерно движется по окружности со скоростью 10 м/с. Найти модуль изменения количества движения за одну четверть периода |ΔQ_1/4|; половину периода |ΔQ_1/2|; целый период |ΔQ₁| (результат вычисления округлить до целого числа);

I: 245.

S: Охотник стреляет из ружья с лодки по направлению её движения. Какую скорость v имела лодка, если она остановилась после быстро следующих друг за другом выстрелов? Масса охотника с лодкой 200 кг, масса заряда 20 г. Скорость вылета дроби и пороховых газов 500 м/с. (Числовой результат определить с точностью до первого знака после запятой.) v = … (м/с).

I: 246.

S: Вагон массой 20 т, движущийся со скоростью 0,3 м/с, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после взаимодействия, если удар неупругий? (Числовой результат определить с точностью до второго знака после запятой.)

I: 247.

S: С лодки массой 200 кг, движущейся со скоростью v =1 м/с, прыгает мальчик массой 50 кг в горизонтальном направлении с кормы в сторону, противоположную движению лодки, со скоростью 6 м/с относительно лодки. Какова скорость v₁ лодки после прыжка мальчика? (Числовой результат определить с точностью до первого знака после запятой.) v₁ = … (м/с).

I: 248.

S:С лодки массой 200 кг, движущейся со скоростью v =1 м/с, прыгает мальчик массой 50 кг в горизонтальном направлении с носа лодки по ходу движения лодки со скоростью 6 м/с относительно лодки. Какова скорость v₁ лодки после прыжка мальчика? (Числовой результат определить с точностью до первого знака после запятой. Будьте внимательны со знаком значения v₁!) v₁ = … (м/с).

I: 249.

S: Мяч массой 100 г, летевший со скоростью20 м/с, ударился о горизонтальную плоскость. Угол падения (угол между направлением скорости и перпендикуляром к плоскости) равен 60 о . Удар абсолютно упругий, а угол отражения равен углу падения. Модуль изменения количества движения равен … (кгּм/с).

I: 250.

S: Какую скорость относительно ракетницы приобретает ракета массой 615 г, если газы массой 15 г вылетают из неё со скоростью 800 м/с?

Скорость ракеты равна … (м/с).

I: 251.

S:Ускорение свободного падения у поверхности Луны g = 1,623 м/с 2 . Радиус Луны R = 1728 км. Вычислить первую космическую скорость v_{косм 1} для Луны. (Результат вычисления округлить до целого числа.) v_{косм 1} = … (м/с).

I: 252.

S:Ускорение свободного падения у поверхности планеты Марс g = 3,71 м/с 2 . Радиус Марса R = 3393 км. Вычислить первую космическую скорость v_косм1 для Марса. (Результат вычисления округлить до целого числа с выбором чётной цифры округления.)

I: 253.

S:Ускорение свободного падения у поверхности Земли g = 9,81 м/с 2 . Радиус Земли R = 6378 км. Вычислить первую космическую скорость v_{косм 1} для Земли. (Результат вычисления округлить до целого числа с выбором чётной цифры округления.) v_{косм 1} = … (м/с).

I: 254.

S:Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру , где — радиус-вектор точки, c = 20 Н/см. Вычислить работу А₁₂ силы при перемещении матер. точки из точки М в точку О (см. рис.); а = 6 см, b = 8 см.

I: 205

S:Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру , где — радиус-вектор точки, c = 20 Н/см. Вычислить работу А₁₂ силы при перемещении матер. точки из точки О в точку М (см. рис.); а = 6 см, b = 8 см.

I: 256.

S:Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру , где — радиус-вектор точки, c = 20 Н/см. Вычислить работу А₁₂ силы при перемещении матер. точки из точки М₁ в точку М₂ (см. рис.); ОМ₁ = b = 8 см, OM₂ = a = 6 см. А₁₂ = … (Дж).

Видео:Физика - движение по окружностиСкачать

Парадокс колеса

На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.

В то же время из школьного курса математики известно, что длина окружности равна:

Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.

Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:

C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.

Но на самом деле она проходит фактически путь вдвое больший.

Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.

Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.

Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.

Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.

Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:

V = w*R, где w — угловая скорость вращения колеса.

Фактически линейная скорость внутренних точек колеса должна описываться уравнением:

V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.

Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.

Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.

Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:

dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R

Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.

С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.

Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.

[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.

Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.

Сазонов Сергей 3 сентября 2019 года в 12:54

Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет.
(конец цитаты)

К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.