Центр числовой окружности совпадает с началом координат на координатной плоскости (3 видео)

Центр числовой окр совпадает с началом координат на координатной плоскости хоу найти корлинаты заданой точки М ( п / 4) и М (п / 3)?

Алгебра | 10 — 11 классы

Центр числовой окр совпадает с началом координат на координатной плоскости хоу найти корлинаты заданой точки М ( п / 4) и М (п / 3).

Содержание

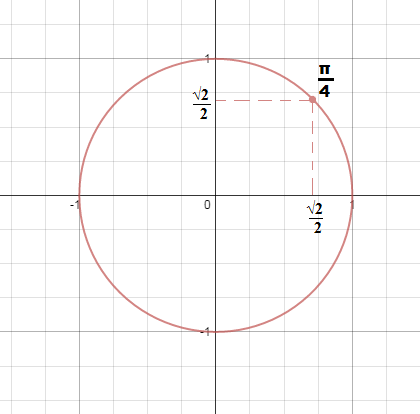
Центр окружности единичного радиуса совпадает с началом координат хOY?
На координатной плоскости отметили точки, у которых координаты – натуральные числа, не превосходящие 9?
На координатной плоскости хОу найдите точку, симметричную данной точке относительно оси х : а)Е(6 ; 0) б)Р( — 2 ; 1)?
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу?
На рисунке изображена координатная плоскость и две прямые в этой плоскости?
На координатной плоскости хОу найдите точку, симметричную данной точке относительно начала координат : б) В(0 ; 8), в)С(7 ; — 1) помогите пожалуста?
Определите знаки коэффициентов k и m, если известно, что график линейной функции y = kx + m, проходит : а)через первый, второй и третий координатные углы плоскости хОу ; б) через первый, второй и четв?
Центр окружности единичного радиуса совпадает с началом координат плоскости х0у?
Окружность касается оси абцисс в начале координат и проходит через точку(0 ; — 4)?
Как на координатной плоскости хОу построить прямую : а) х = а ; б) у = b?
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
п.2. Числовая окружность
п.3. Градусная и радианная мера угла
п.4. Свойства точки на числовой окружности
п.5. Интервалы и отрезки на числовой окружности
п.6. Примеры
Декартовы координаты точек плоскости. Уравнение окружности
Числовая ось
Прямоугольная декартова система координат на плоскости
Формула для расстояния между двумя точками координатной плоскости
Уравнение окружности на координатной плоскости
📽️ Видео

Видео:№ 5.2- Алгебра 10-11 класс МордковичСкачать

Центр окружности единичного радиуса совпадает с началом координат хOY?

Центр окружности единичного радиуса совпадает с началом координат хOY.

Видео:№ 5.3- Алгебра 10-11 класс МордковичСкачать

На координатной плоскости отметили точки, у которых координаты – натуральные числа, не превосходящие 9?

На координатной плоскости отметили точки, у которых координаты – натуральные числа, не превосходящие 9.

Найдите сумму координат этих точек.

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

На координатной плоскости хОу найдите точку, симметричную данной точке относительно оси х : а)Е(6 ; 0) б)Р( — 2 ; 1)?

На координатной плоскости хОу найдите точку, симметричную данной точке относительно оси х : а)Е(6 ; 0) б)Р( — 2 ; 1).

Видео:Числовая окружность на координатной плоскости | Алгебра 10 класс #10 | ИнфоурокСкачать

Центр окружности единичного радиуса совпадает с началом координат плоскости хОу?

Центр окружности единичного радиуса совпадает с началом координат плоскости хОу.

Принадлежит ли дуге Р1Р2, где Р1 ( — 5П / 6), Р2 (П / 4), точки М1 ( — 1 ; 0) ; М2 (0 ; — 1) ; М3 (корень из 3 / 2 ; — 1 / 2), М3 ( минус корень из 2 / 2 ; минус корень из 2 / 2) Помогите, с объяснением, пожалуйста!

Видео:10 класс, 11 урок, Числовая окружностьСкачать

На рисунке изображена координатная плоскость и две прямые в этой плоскости?

На рисунке изображена координатная плоскость и две прямые в этой плоскости.

Найдите квадрат расстояния от точки C до начала координат.

Видео:№ 5.1- Алгебра 10-11 класс МордковичСкачать

На координатной плоскости хОу найдите точку, симметричную данной точке относительно начала координат : б) В(0 ; 8), в)С(7 ; — 1) помогите пожалуста?

На координатной плоскости хОу найдите точку, симметричную данной точке относительно начала координат : б) В(0 ; 8), в)С(7 ; — 1) помогите пожалуста.

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Определите знаки коэффициентов k и m, если известно, что график линейной функции y = kx + m, проходит : а)через первый, второй и третий координатные углы плоскости хОу ; б) через первый, второй и четв?

Определите знаки коэффициентов k и m, если известно, что график линейной функции y = kx + m, проходит : а)через первый, второй и третий координатные углы плоскости хОу ; б) через первый, второй и четвёртый координатные углы плоскости хОу ; в) через первый, третий и четвёртый координатные углы плоскости хОу ; г) через второй, третий и четвёртый координатные углы плоскости хОу ;

Видео:10 класс - Алгебра - Числовая окружность на координатной плоскостиСкачать

Центр окружности единичного радиуса совпадает с началом координат плоскости х0у?

Центр окружности единичного радиуса совпадает с началом координат плоскости х0у.

Принадлежит ли дуге Р1Р2 где Р1( — 5pi / 6) Р2(pi / 4) точки М1( — 1 ; 0) М2(0 ; — 1) М3( ; — 1 / 2) М4( — ).

Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Окружность касается оси абцисс в начале координат и проходит через точку(0 ; — 4)?

Окружность касается оси абцисс в начале координат и проходит через точку(0 ; — 4).

Составить уравнение этой окружности и найти её точки пересечения с биссектрисами координатных углов.

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Как на координатной плоскости хОу построить прямую : а) х = а ; б) у = b?

На этой странице сайта, в категории Алгебра размещен ответ на вопрос Центр числовой окр совпадает с началом координат на координатной плоскости хоу найти корлинаты заданой точки М ( п / 4) и М (п / 3)?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Центр числовой окружности совпадает с началом координат на координатной плоскости

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0).
Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0.
Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°.
Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr.
Длина дуги AB: (l_=frac=frac=frac.)
Тогда радианная мера угла: $$ angle AOB=frac<l_>=frac=frac $$

30°	45°	60°	90°	120°	135°	150°	180°	270°	360°
(frac)	(frac)	(frac)	(frac)	(frac)	(frac)	(frac)	(pi)	(frac)	(2pi)

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t).
При t=0, M(0)=A.
При t>0 двигаемся по окружности против часовой стрелки, описывая дугу
⌒ AM=t. Точка M — искомая.
При t Например:

Отметим на числовой окружности точки, соответствующие (frac, frac, frac, frac, pi), а также (-frac, -frac, -frac, -frac, -pi)
Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac, frac, frac), и (-frac).
Все четыре точки совпадают, т.к. begin Mleft(fracright)=Mleft(frac+2pi kright)\ frac-2pi=-frac\ frac+2pi=frac\ frac+4pi=frac end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
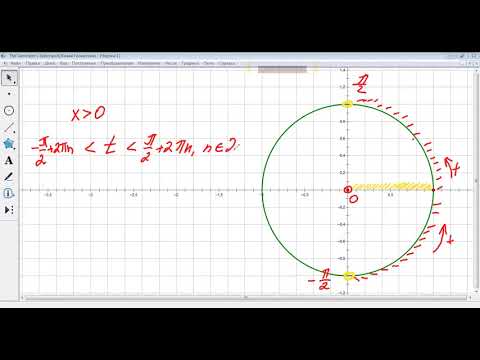
$$ -frac lt t lt frac $$ а также, с учетом периода $$ -frac+2pi klt tltfrac+2pi k $$
Интервал
$$ -frac leq t leq frac $$ а также, с учетом периода $$ -frac+2pi kleq tleqfrac+2pi k $$
Полуинтервал
$$ -frac leq t ltfrac $$ а также, с учетом периода $$ -frac+2pi kleq tltfrac+2pi k $$

п.6. Примеры

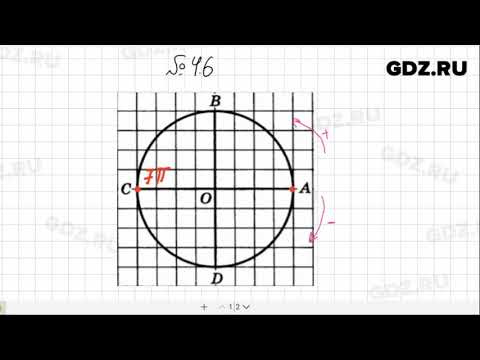
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^=frac.\ EC=60^=frac.\ AE=EC+CD=90^+30^=120^=frac.\ ED=EC+CD=60^+90^=150^=frac. end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; frac; frac; frac).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac=-90^, frac=135^\ frac=210^, frac=315^ end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; 5pi; frac; frac).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π.
Далее – действуем, как в примере 2. begin -frac=fraccdotpi=-6pi+fracrightarrow frac=90^\ 5pi=4pi+pirightarrow pi=180^\ frac=fracpi=3pi-fracrightarrow pi-frac=frac\ frac=fracpi=7pi-fracrightarrow pi-frac=frac end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ fracapprox frac=4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(fraclt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.

$$ frac $$	$$ -frac+2pi k $$
Четыре базовых точки, через каждые 90°	Две базовых точки, через каждые 180°
$$ frac+frac $$	$$ -frac $$
Три базовых точки, через каждые 120°	Пять базовых точек, через каждые 72°

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

Видео:Числовая окружность на координатной плоскостиСкачать

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:№ 5.4- Алгебра 10-11 класс МордковичСкачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:Прямоугольная система координат. Координатная плоскость. 6 класс.Скачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.