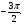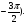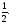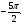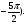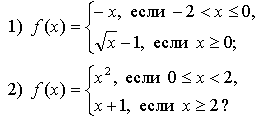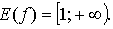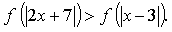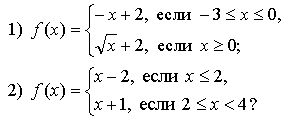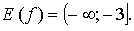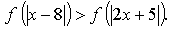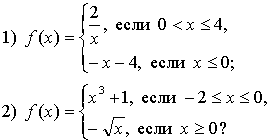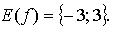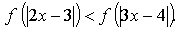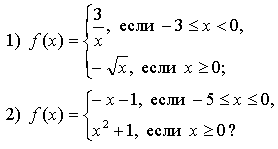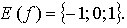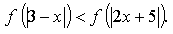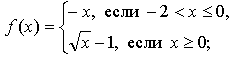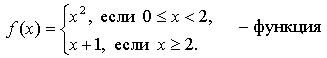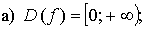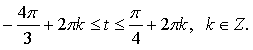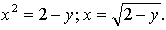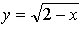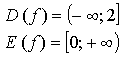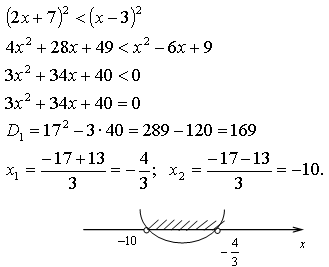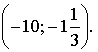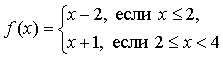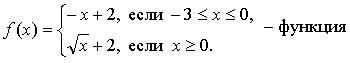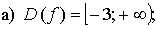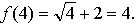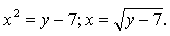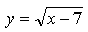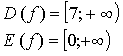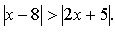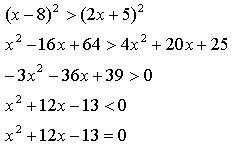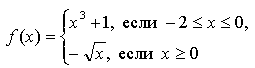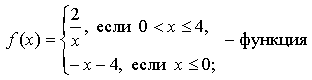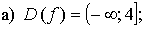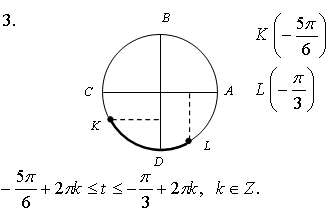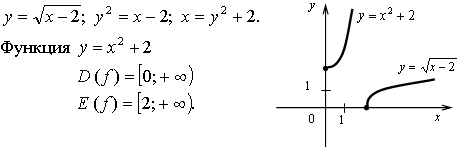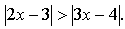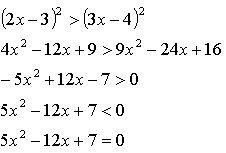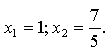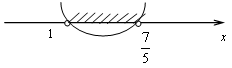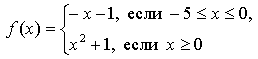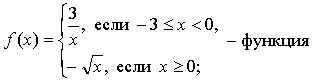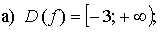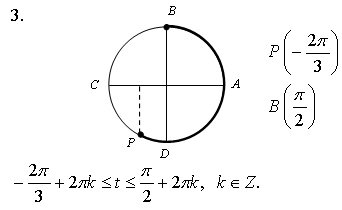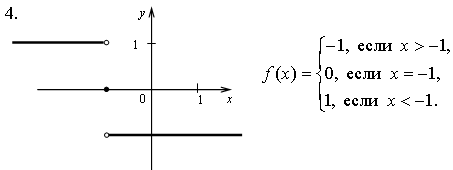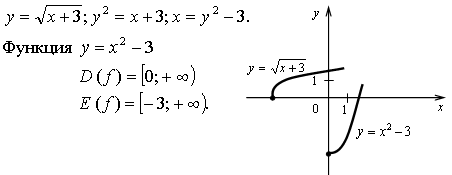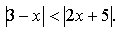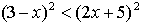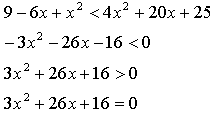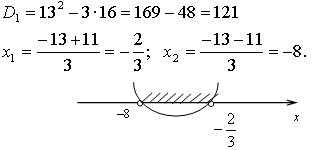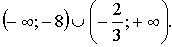Контрольный срез по теме «Тригонометрический круг» предназначен для проверки знаний учащихся 10 класса. В процессе выполнения заданий учащимся необходимо показать свои умения определять по кругу табличные значения тригонометрических функций, отмечать на тригонометрическом круге точки, соответствующие данным углам, а так же решать простейшие тригонометрические неравенства.
- Просмотр содержимого документа «Контрольный срез «Тригонометрический круг»»
- Контрольные работы по алгебре иначалам анализа 10 класс учебно-методический материал по алгебре (10 класс) на тему
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Контрольная работа № 1 по теме «Числовая окружность»
- 🔥 Видео
Просмотр содержимого документа
«Контрольный срез «Тригонометрический круг»»
Контрольный срез по материалу курса алгебры и начал анализа 10 класса
Отметьте на тригонометрическом круге точки, соответствующие углам:
а) 
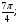
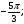
а) 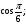
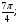
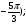
Укажите множество точек окружности, для которых:
а) cost =
а) 2cos60 o – tg 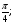
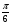
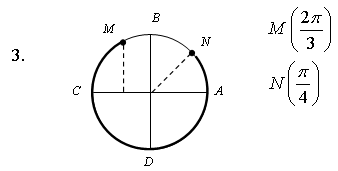
Укажите дугу окружности, множество точек которой удовлетворяет условию:
а) cost 
Найдите наименьшее и наибольшее значение выражения 0,5cost +2.
Контрольный срез по материалу курса алгебры и начал анализа 10 класса
Отметьте на тригонометрическом круге точки, соответствующие углам:
а) 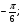
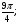
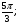
а) cos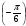
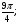
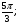
Укажите множество точек окружности, для которых:
а) cost = 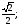
Укажите дугу окружности, множество точек которой удовлетворяет условию:
а) cos t 
Найдите наименьшее и наибольшее значение выражения 3sin t – 1 .
Оценка «3» , если набрано 10 – 12 баллов; Оценка «4» , если набрано 13 – 15 баллов;
Оценка «5» , если набрано 16 — 20 баллов.
Видео:Тригонометрическая окружность. Как выучить?Скачать

Контрольные работы по алгебре иначалам анализа 10 класс
учебно-методический материал по алгебре (10 класс) на тему
В данном документе содержатся все контрольные работы по алгебре и началам анализа для 10 класса.
Видео:Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать

Скачать:
| Вложение | Размер |
|---|---|
| КР 1 | 45 КБ |
| КР 2 | 42.5 КБ |
| КР 3 | 50 КБ |
| КР 4 | 43.5 КБ |
| КР 5 | 49.5 КБ |
| КР 6 | 52 КБ |
| Кр 7 | 41.5 КБ |
| КР 8 | 43.5 КБ |
| Итоговая КР | 49.5 КБ |
Видео:Тригонометрия. 10 класс. Вебинар | МатематикаСкачать

Предварительный просмотр:
Контрольная работа №1
Определение числовой функции. Числовая окружность
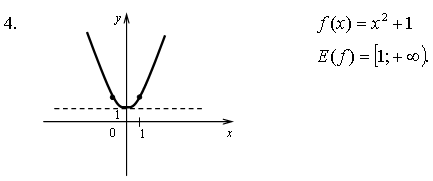
1. Найдите область определения функции: .
2. Найдите область значений функции: .
3. Найдите на числовой окружности точку:
4. Найдите наименьшее положительное и наибольшее отрицательное числа, которым на числовой окружности соответствует точка с координатами:
5. Найдите на числовой окружности тачки с абсциссой или ординатой, удовлетворяющей заданному неравенству, и запишите (с помощью двойного неравенства), каким числам t они соответствуют:
Контрольная работа №1
Определение числовой функции. Числовая окружность
1. Найдите область определения функции: .
2. Найдите область значений функции: .
3. Найдите на числовой окружности точку:
4. Найдите наименьшее положительное и наибольшее отрицательное числа, которым на числовой окружности соответствует точка с координатами:
5. Найдите на числовой окружности тачки с абсциссой или ординатой, удовлетворяющей заданному неравенству, и запишите (с помощью двойного неравенства), каким числам t они соответствуют:
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Предварительный просмотр:
Контрольная работа №2
Определение тригонометрических функций
А1. Найдите значение выражения:
А2. Решите уравнение: .
А3. Найдите наименьшее и наибольшее значение выражения: .
В1. Укажите все значения t , при которых выражение не имеет смысла.
В2. Определите знак выражения: .
С1. Решите неравенство: .
Нормы оценок: «3»- любые 3А, 4» — 3А + 1В, «5» — 2А + 2В или 2А + 1В + 1С.
Контрольная работа №2
Определение тригонометрических функций
А1. Найдите значение выражения:
А2. Решите уравнение: .
А3. Найдите наименьшее и наибольшее значение выражения: .
В1. Укажите все значения t , при которых выражение не имеет смысла.
В2. Определите знак выражения: .
С1. Решите неравенство: .
Нормы оценок: «3»- любые 3А, 4» — 3А + 1В, «5» — 2А + 2В или 2А + 1В + 1С.
Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Предварительный просмотр:
Контрольная работа №3
Свойства и графики тригонометрических функций
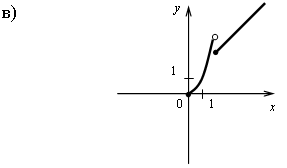
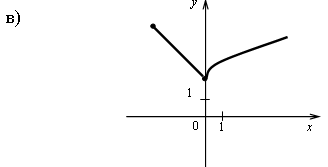
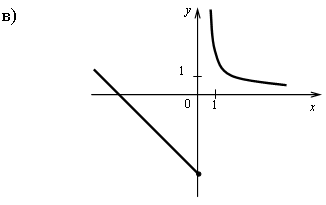
А1. Постройте график функции: .
А2. Найдите множество значений функции .
А3. Выяснить, является ли данная функция четной или нечетной:
А4. Докажите, что функция является периодической с периодом .
В1. Сравните числа: .
В2. Найдите наибольшее и наименьшее значение функции на отрезке .
С1. Построить график функции у = |sin x| +1
Нормы оценок: «3»- любые 3А, «4» — 3А + 1В, «5» — 2А + 2В или 2А + 1В + 1С.
Контрольная работа №3
Свойства и графики тригонометрических функций
А1. Постройте график функции: .
А2. Найдите множество значений функции .
А3. Выясните, является ли данная функция четной или нечетной: .
А4. Докажите, что функция у = tg 3x является периодической с периодом .
В1. Сравните числа:
В2. Найдите наибольшее и наименьшее значение функции на отрезке .
С1. Постройте график функции .
Нормы оценок: «3»- любые 3А, «4» — 3А + 1В, «5» — 2А + 2В или 2А + 1В + 1С.
Видео:Контрольная работа 1Скачать

Предварительный просмотр:
Контрольная работа №4
А1. Решите уравнения:
А2. Решите уравнения:
В1. Решите уравнение .
В2. Решите уравнение: .
С1. Найдите корни уравнения на промежутке .
Нормы оценок: «3» — любые 3А, «4» — 2А + 1В, «5» — 3А + 2В или 2А + 1В +1С.
Контрольная работа №4
А1. Решите уравнения:
А2. Решите уравнения:
В1. Решите уравнение .
В2. Решите уравнение: .
С1. Найдите корни уравнения на промежутке .
Нормы оценок: «3» — любые 3А, «4» — 2А + 1В, «5» — 3А + 2В или 2А + 1В +1С.
Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Предварительный просмотр:
Контрольная работа №5
Преобразование тригонометрических выражений
А1. Решите уравнения:
А2. Докажите тождество: .
А3. Преобразуйте произведение в сумму
В1. Найдите наименьшее и наибольшее значения функции .
В2. Решите уравнение .
С1. Найдите значение выражения если .
Нормы оценок: «3» — любые 3А, «4» — 2А + 1В, «5» — 3А + 2В или 2А + 1В +1С.
Контрольная работа №5
Преобразование тригонометрических выражений
А1. Упростите выражение:
А2. Докажите тождество: .
А3. Преобразуйте произведение в сумму
В1. Найдите наименьшее и наибольшее значения функции .
В2. Решите уравнение .
С1. Найдите значение выражения если известно, что .
Нормы оценок: «3» — любые 3А, «4» — 2А + 1В, «5» — 3А + 2В или 2А + 1В +1С.
Видео:10 класс. Контрольная №3 (из 9). Тема: Тригонометрическая функция, тригонометрическая окружность! 🙂Скачать

Предварительный просмотр:
Контрольная работа №6
Определение производной и ее вычисление
А1. Найдите производную функции:
А2. Найдите производную функции: .
А3. Найдите значение производной функции .
В1. Найдите значения х , при которых значения производной функции отрицательны.
В2. Решите уравнение , если .
С1. Задайте формулой хотя бы одну функцию , если
Нормы оценок: «3» — любые 5А, «4» — 4А + 1В, «5» — 5А + 2В или 4А + 1В +1С.
Контрольная работа №6
Определение производной и ее вычисление
А1. Найдите производную функции:
А2. Найдите производную функции: .
А3. Найдите значение производной функции .
В1. Найдите значения х , при которых значения производной функции отрицательны.
В2. Решите уравнение , если .
С1. Задайте формулой хотя бы одну функцию , если
Нормы оценок: «3» — любые 5А, «4» — 4А + 1В, «5» — 5А + 2В или 4А + 1В +1С.
Видео:Контрольная работа 1 | ТригонометрияСкачать

Предварительный просмотр:
Контрольная работа №7
Построение графиков функций с помощью производной
А1. Найдите промежутки возрастания и убывания функции:
А2. Найдите критические точки функции . Определите, какие из них являются точками максимума, а какие – точками минимума .
А3. Исследуйте функцию и постройте ее график:
В1. Исследуйте функцию и постройте ее график:
С1. Сколько корней имеет уравнение .
Нормы оценок: «3» — любые 3А, «4» — 3А + 1В, «5» — 5А + 1В или 3А + 1В +1С.
Контрольная работа №7
Построение графиков функций с помощью производной
А1. Найдите промежутки возрастания и убывания функции:
А2. Найдите критические точки функции . Определите, какие из них являются точками максимума, а какие – точками минимума .
А3. Исследуйте функцию и постройте ее график:
В1. Исследуйте функцию и постройте ее график:
С1. Сколько корней имеет уравнение .
Нормы оценок: «3» — любые 3А, «4» — 3А + 1В, «5» — 5А + 1В или 3А + 1В +1С.
Видео:ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Предварительный просмотр:
Контрольная работа №8
Применение производной к исследованию функций
А1. Найдите наибольшее и наименьшее значения заданной функции на заданном отрезке:
А2. Найдите наименьшее и наибольшее значения функции на отрезке .
В1. Докажите, что функция возрастает на всей числовой оси.
В2. Найдите наименьшее и наибольшее значения функции на отрезке .
С1. Найти число, которое превышало бы свой квадрат на максимальное значение.
Нормы оценок: «3» — любые 3А, «4» — 2А + 1В, «5» — 2А + 2В или 2А + 1В +1С.
Контрольная работа №8
Применение производной к исследованию функций
А1. Найдите наибольшее и наименьшее значения заданной функции на заданном отрезке:
А2. Найдите наименьшее и наибольшее значения функции на отрезке .
В1. Докажите, что функция убывает на всей числовой оси.
В2. Найдите наименьшее и наибольшее значения функции на отрезке .
С1. Число 18 разбить на такие два слагаемых, чтобы сумма их квадратов была наименьшей.
Нормы оценок: «3» — любые 3А, «4» — 2А + 1В, «5» — 2А + 2В или 2А + 1В +1С.
Видео:Разбор контрольной работы по алгебре 10 класс. Тригонометрические уравнения. МордковичСкачать

Предварительный просмотр:
Контрольная работа №9
Итоговая контрольная работа
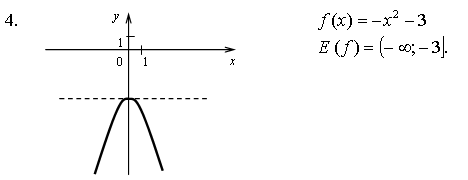
А1. Найдите область определения каждой из функций: .
А2. Найдите область значений функции .
А3. Решите уравнение: .
А4. Найдите производную функции: .
В1. Найдите наименьшее и наибольшее значения функции на отрезке .
С1. Напишите уравнения касательных к кривой , проходящих через точку .
Нормы оценок: «3» — любые 3А, «4» — 3А + 1В, «5» — 6А + 1В или 2А + 1В +1С.
Контрольная работа №9
Итоговая контрольная работа
А1. Найдите область определения каждой из функций: .
А2. Найдите область значений функции .
А3. Решите уравнение: .
А4. Найдите производную функции: .
В1. Найдите наименьшее и наибольшее значения функции на отрезке .
С1. В каких точках касательные к кривой параллельны прямой ?
Нормы оценок: «3» — любые 3А, «4» — 3А + 1В, «5» — 6А + 1В или 2А + 1В +1С.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

По теме: методические разработки, презентации и конспекты
контрольная работа по алгебре №1 8 класс
Работа состоит из 2 вариантов, на 25 минут по теме «Сложение и вычитание алгебраических дробей с разными знаменателями».
Итоговая контрольная работа по алгебре в 7 классах
В работе представлены пояснительная записка, в которой отмечена нормативно-правовая база, структура контрольной работы, критерии оценивания, использованная литература. Также текст контрольной работы в.
Промежуточная аттестация: итоговая контрольная работа по алгебре в 7 классах
В работе представлены пояснительная записка, в которой отмечена нормативно-правовая база, структура контрольной работы, критерии оценивания, использованная литература. Также текст контрольной работы в.
итоговая (годовая) контрольная работа по алгебре в 10 классе. УМК Колягин или Алимов.
Цель работы: проверить уровень математической подготовки учащихся 10 класса с позиций Единого Го.
контрольные работы по алгебре в 7 классе к учебнику Макарычев Ю.Н. и др. ( ИЗ АВТОРСКОЙ ПРОГРАММЫ ПО АЛГЕБРЕ. 2012ГОДА)
Данная работа взята из авторской программы по алгебре для 7-9классов издательства «Просвещение » 2012года. Удобно использовать для рабочей программы .
Комплект тематических контрольных работ по алгебре за 7 класс к УМК «Алгебра 7кл», Ю.Н. Макарычев, Н.Г. Миндюк и другие (под редакцией С.А.Теляковского)
Данный комплект содержит комплект тематических контрольных работ с №1 по №9 + №10 (годовая) – к УМК «Алгебра 7кл», Ю.Н. Макарычев, Н.Г. Миндюк и другие (под редакцией С.А.
Контрольно-измерительные материалы для проведения итоговой контрольной работы по алгебре в 7 классе.
Материал может использоваться для проведения переводного экзамена по алгебре в 7 классе.Критерии по оцениванию:Каждый пункт оценивается как отдельное задание.Все задания решены верно &nda.
Видео:Контрольная работа по тригонометрии 1Скачать

Контрольная работа № 1 по теме «Числовая окружность»
Контрольная работа № 1 (1 час)
Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
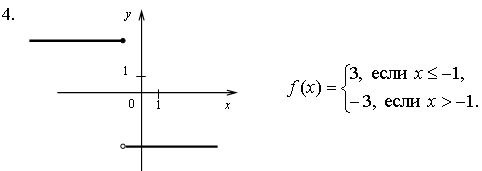
1. Задает ли указанное правило функцию
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0, 1, 3, -1;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
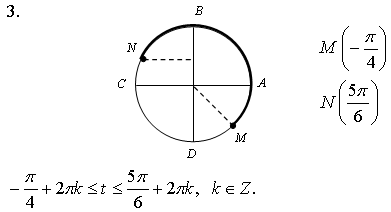
3. На числовой окружности взяты точки Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
4. Задайте аналитически и постройте график функции 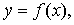
5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.
6. Известно, что функция убывает на R. Решите неравенство
1. Задает ли указанное правило функцию
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках -4, -2, 0, 4;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
4. Задайте аналитически и постройте график функции 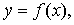
5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.
6. Известно, что функция возрастает на R. Решите неравенство
1. Задает ли указанное правило функцию
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках -1, 0, 2, 5;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге KL. Сделайте чертёж.
4. Задайте аналитически и постройте график функции 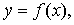
5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.
6. Известно, что функция убывает на R. Решите неравенство
1. Задает ли указанное правило функцию
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках -6, -3, 0, 4;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге PB. Сделайте чертёж.
4. Задайте аналитически и постройте график функции 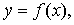
5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.
6. Известно, что функция возрастает на R. Решите неравенство
Рекомендации по оцениванию контрольной работы
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума — до первой черты, задания среднего уровня — между первой и второй чертой, задания уровня выше среднего — после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение только заданий обязательного минимума — оценка «3»; за успешное выполнение заданий обязательного минимума и одного дополнительного (после первой или второй черты) — оценка «4»; за успешное выполнение заданий всех трех уровней — оценка «5». При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Решение контрольной работы
1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.
В случае
условия не соблюдаются: f(0) = 0 и f(0) = -1.
б) 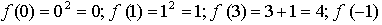
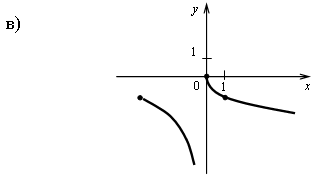
г) на [0; 2) и на [2; +) функция возрастает, в точке х = 2 функция имеет разрыв.
2. 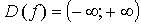
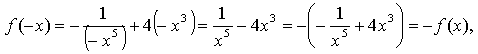
5. у = 2 — х 2 Квадратичная функция определена и убывает при х 0, значит, существует обратная функция: у = 2 — х 2 ;
Функция
6. у = f(х) убывает на R.
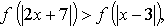
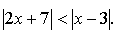
Ответ:
1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.
В случае
условия не соблюдаются: f(2) = 0 и f(2) = 3.
б) f(-4) — не определено;
г) на 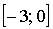
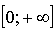
2. 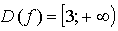
5. у = х 2 + 7. Квадратичная функция определена и возрастает при х 0, значит, существует обратная функция: у = х 2 + 7;
Функция
6. f(х) возрастает на R.
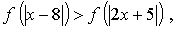
Возведем обе части в квадрат:
По теореме Виета х1 = -13; х2 = 1.
1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.
В случае
условия не соблюдаются: f(0) = 1 и f(0) = 0.
б) 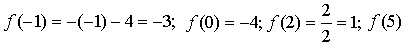
г) на (-; 0] и на (0; 4] функция убывает, в точке х = 0 функция имеет разрыв.
2. 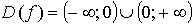
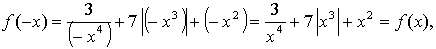
5. 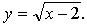
6. у = f(х) убывает на R.
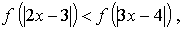
Возведем обе части в квадрат:
По теореме Виета
1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.
В случае
условия не соблюдаются: f(0) = -1 и f(0) = 1.
б) f(-6) — не определено;
г) на [-3; 0) и на [0; +) функция убывает, в точке х = 0 функция имеет разрыв.
2. 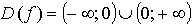
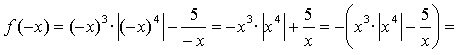
функция f(х) — нечетная.
5. 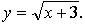
6 у = f(х) возрастает на R.
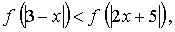
Возведем обе части в квадрат:
Ответ:
🔥 Видео
Математика это не ИсламСкачать

Тригонометрическая окружностьСкачать

Алгебра, 10 класс, Подготовка к контрольной работе по теме "Тригонометрические функции"(Ш.А. Алимов)Скачать

Как искать точки на тригонометрической окружности.Скачать

Формулы приведения с нуля за 15 минут!Скачать

Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать