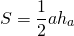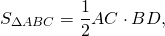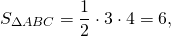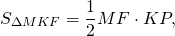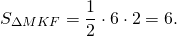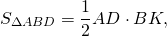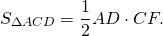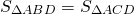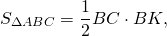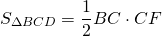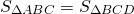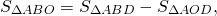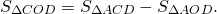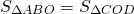Равновеликие треугольники — это треугольники, которые имеют одинаковую площадь.
Равновеликие треугольники могут быть равными (так как равные треугольники имеют равные площади), но также могут иметь разные стороны и разные углы.

Можно заметить, что если сторону треугольника увеличить в k раз, а высоту, проведенную к этой стороне, уменьшить в k раз, то получим треугольник, равновеликий данному.
Равновеликие треугольники в треугольнике
Медиана делит треугольник на два равновеликих треугольника.
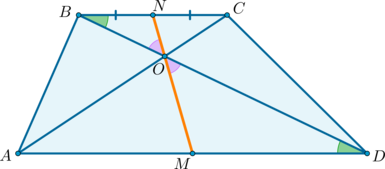
Равновеликие треугольники в трапеции
При пересечении диагоналей в произвольной трапеции ABCD образуется три пары равновеликих треугольников:


BK=CF (как высоты трапеции), следовательно,

Так как площади треугольников ABD и ACD равны (по доказанному), то и
Таким образом, треугольники , образованные боковыми сторонами и диагоналями трапеции, имеют равные площади.
Видео:Геометрия 8 класс (Урок№4 - Трапеция)Скачать

Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
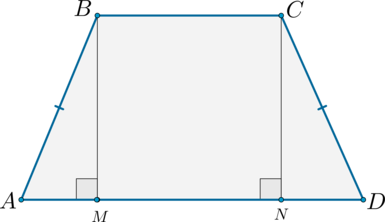
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Видео:8 класс, 6 урок, ТрапецияСкачать

Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Трапеция
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ) .
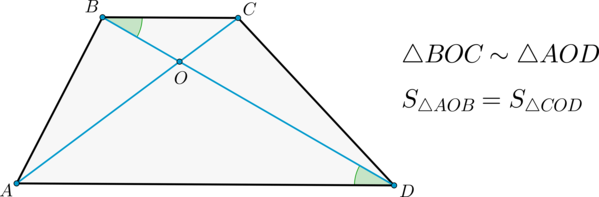
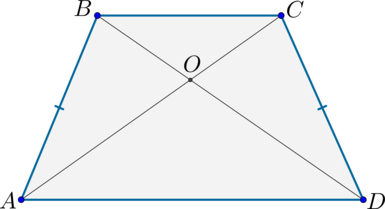
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
1) Т.к. (ADparallel BC) , то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB) , следовательно, (angle BAD +angle ABC=180^circ) .
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD) .
Определение
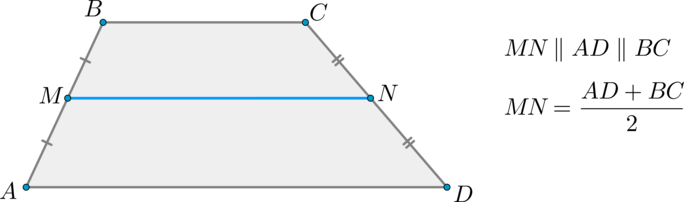
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
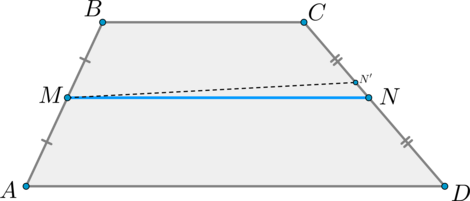
Проведем через точку (M) прямую (MN’parallel AD) ( (N’in CD) ). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB) ) точка (N’) — середина отрезка (CD) . Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
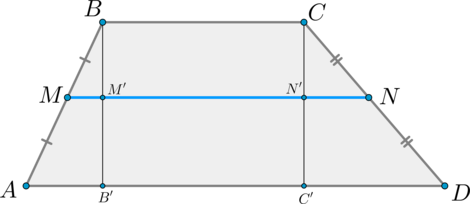
Проведем (BB’perp AD, CC’perp AD) . Пусть (BB’cap MN=M’, CC’cap MN=N’) .
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle ABB’) , (NN’) — средняя линия (triangle DCC’) . Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD) , то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B) . Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC) .
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
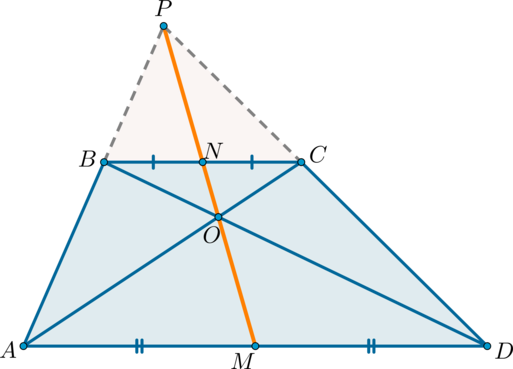
1) Докажем, что точки (P) , (N) и (M) лежат на одной прямой.
Проведем прямую (PN) ( (P) – точка пересечения продолжений боковых сторон, (N) – середина (BC) ). Пусть она пересечет сторону (AD) в точке (M) . Докажем, что (M) – середина (AD) .
Рассмотрим (triangle BPN) и (triangle APM) . Они подобны по двум углам ( (angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac=dfrac]
Рассмотрим (triangle CPN) и (triangle DPM) . Они подобны по двум углам ( (angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac=dfrac]
Отсюда (dfrac=dfrac) . Но (BN=NC) , следовательно, (AM=DM) .
2) Докажем, что точки (N, O, M) лежат на одной прямой.
Пусть (N) – середина (BC) , (O) – точка пересечения диагоналей. Проведем прямую (NO) , она пересечет сторону (AD) в точке (M) . Докажем, что (M) – середина (AD) .
(triangle BNOsim triangle DMO) по двум углам ( (angle OBN=angle ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac=dfrac]
Аналогично (triangle CONsim triangle AOM) . Значит: [dfrac=dfrac]
Отсюда (dfrac=dfrac) . Но (BN=CN) , следовательно, (AM=MD) .
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию (ABCD) .
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD) , то (BMparallel CN) ; (ADparallel BC) , тогда (MBCN) – параллелограмм, следовательно, (BM = CN) .
Рассмотрим прямоугольные треугольники (ABM) и (CDN) . Так как у них равны гипотенузы и катет (BM) равен катету (CN) , то эти треугольники равны, следовательно, (angle DAB = angle CDA) .
2)
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD) . Следовательно, (AC=BD) .
3) Т.к. (triangle ABD=triangle ACD) , то (angle BDA=angle CAD) . Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
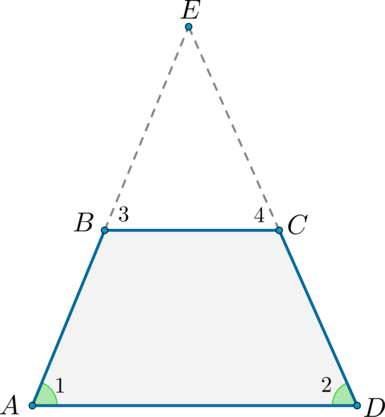
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
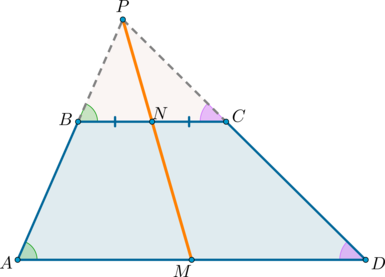
Рассмотрим трапецию (ABCD) , такую что (angle A = angle D) .
Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2) , то треугольник (AED) равнобедренный и (AE = ED) . Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB) . Аналогично равны углы (2) и (4) , но (angle 1 = angle 2) , тогда (angle 3 = angle 1 = angle 2 = angle 4) , следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC) .
В итоге (AB = AE — BE = DE — CE = CD) , то есть (AB = CD) , что и требовалось доказать.
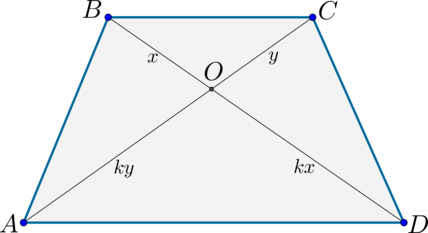
2) Пусть (AC=BD) . Т.к. (triangle AODsim triangle BOC) , то обозначим их коэффициент подобия за (k) . Тогда если (BO=x) , то (OD=kx) . Аналогично (CO=y Rightarrow AO=ky) .
Т.к. (AC=BD) , то (x+kx=y+ky Rightarrow x=y) . Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA) .
Таким образом, по первому признаку (triangle ABD=triangle ACD) ( (AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD) , чтд.
🔍 Видео
Геометрия 8 класс (Урок№16 - Средняя линия треугольников и трапеции.)Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Трапеция, решение задач. Вебинар | МатематикаСкачать

Задача 15 ОГЭ: подобные треугольники в трапецииСкачать

КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

все свойства трапецииСкачать

Теорема о средней линии трапецииСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Трапеция. Отношение площадей треугольников. Свойства диагоналей трапецииСкачать

Как доказать У равнобедренной трапеции углы при основаниях равны и диагонали равныСкачать

№1,16 Свойства трапеции. Планиметрия ЕГЭ 2023 по математикеСкачать

Геометрия 8. Урок 7 - Средняя линия треугольника и трапецииСкачать

Все свойства трапеции ✔️ #умскул_профильнаяматематика #никитасалливан #егэ #егэ2023Скачать