Иногда кажется, что некоторые математические темы изучены вдоль и поперек, например, треугольники. Ну что в этих треугольниках может быть нового и интересного? Тем не менее, даже такие, казалось бы, тривиальные объекты могут предстать под неожиданным углом. Давайте возьмем какую-нибудь простенькую задачку и попробуем ее решить. Постараемся найти треугольник с целочисленными сторонами, медианами и площадью. Мало ли, вдруг у нас получится.
- Как перечислить все треугольники?
- Причем тут алгебра?
- Почему это все бесполезно?
- В заключение
- Треугольник Паскаля — формула, свойства и применение
- Основная формула
- История открытия
- Отличительные черты
- Общие свойства
- Секреты треугольника
- Полномочия двойки
- Силы одиннадцати
- Совершенные квадраты
- Комбинаторные варианты
- Действия с биномами
- Операции над множествами
- Собственное подмножество и булеан множества
- Свойства операций над множествами
- 🎦 Видео
Как перечислить все треугольники?
Даже несмотря на то, что некоторые множества содержат бесконечное количество элементов, они являются перечислимыми. Например, множество четных чисел может быть перечислено с помощью очень простого алгоритма — для любого n выдаем 2n и все. Во многом такая простота перечислимости некоторых множеств обусловлена тем, что элементы как-то упорядочены. Фактически, перечислить — значит пронумеровать, например, 2 — это первое четное число, 6 — третье. Но можем ли мы проделать то же самое с треугольниками? Если задавать треугольники с помощью кортежей вида a,b,c, то можем ли мы сказать, что треугольник 1,1,1 является первым, а треугольник 3,2,2 — четвертым или восьмым или еще каким-нибудь номером? Оказывается, можем.
Первое, что нужно придумать — это то как упорядочить множество треугольников. Первое, что приходит в голову — взять треугольник с какой-нибудь одной фиксированной стороной и выписать другие треугольники, стороны которого не меньше заданной. Например, так:
Как видим, первая сторона неизменна, а третья не превосходит суммы двух первых, на графике это будет выглядеть так:
Перед нами две ступенчатые функции, а значит мы можем задать стороны всех таких треугольников следующим образом:
Если заменить тройку на а
на
, то получим следующее:
Теперь любой треугольник можно изображать в виде точки на координатной плоскости, преобразуя стороны треугольников в координаты по двум простым формулам:
Чтобы перейти от координат к номерам достаточно воспользоваться канторовской нумерацией:
Или, если вместо координат использовать стороны треугольника:
Не знаю как вы, а я очень удивился, когда понял, что у каждого треугольника с целыми сторонами может быть свой номер. Есть что-то необычное в том, что подмножества треугольников, например, равнобедренные, могут выглядеть вот так:
Причем тут алгебра?
Очень похоже, что номера равнобедренных треугольников представляют собой множество парабол, нарисованных на одном графике. Так и есть, каждая из них может быть задана уравнением вида:
То же самое можно сказать и про многие другие подмножества треугольников. Например, вот так будут выглядеть треугольники с целыми, четными сторонами и одной целой медианой, проведенной к стороне :
На графике с координатами расположено множество кубических функций вида:
Не знаю, можно ли задать функции для всех кубических функций, но некоторые из них могут быть заданы, например, так:
Можно взять какую-то отдельную из них, например при j=0 и получить следующие формулы для координат треугольников:
Используя данные координаты можем задать функции для сторон и медианы:
Мы можем попробовать провернуть то же самое для треугольников, у которых две целые медианы:
Хоть этого и не видно на графике, но координаты треугольников с двумя целыми медианами задаются кубическими, квадратичными и линейными функциями. К сожалению, не могу привести все выкладки куда−то потерялись записи.
Если мы нарисуем график для треугольников с тремя целыми медианами, то получим следующее:
Таких треугольников очень мало, они очень сильно разрежены, но любопытно, что если найти хотя бы один такой треугольник, то все последующие могут быть заданы как:
Например, если взять треугольник 136, 170, 172 и умножить его стороны на 5, то мы снова получим треугольник с целыми сторонами и медианами.
Почему это все бесполезно?
Сначала кажется, что нумерация треугольников это шажок в сторону создания системы диофантовых уравнений, которые определяли бы стороны треугольников с целыми сторонами и медианами. Затем эти уравнения можно было бы подставить в формулу Герона и потом попытаться доказать возможность получения или неполучения треугольников с целой площадью. Но, к сожалению, нумерация треугольников абсолютно бесполезна в этом направлении. Все дело в том, что сама задача поиска треугольников с целыми сторонами и медианами связана с простыми числами. Сначала это кажется не совсем очевидным, но если следующее тождество является верным
то медиана не может быть целым числом. А это значит, что сама задача поиска треугольников с целыми сторонами и медианами наверняка может быть переведена на язык теории чисел, правда не знаю как.
В заключение
Сама идея того, что можно навести какой-никакой порядок в неупорядоченных множествах, очень любопытна. Например, можно попытаться каким-нибудь образом упорядочить матрицы из натуральных чисел, или графы определенного типа. Можно ли извлечь какую-то пользу от такого упорядочивания, это уже другой вопрос.
Видео:Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

Треугольник Паскаля — формула, свойства и применение
Видео:Удивительный треугольник Паскаля | Лекции по математике – Яков Ерусалимский | Научпоп | НаукаPROСкачать

Основная формула
Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:
- В центре верхней части листа ставится цифра «1».
- В следующем ряду — две единицы слева и справа от центра (получается треугольная форма).
- В каждой последующей строке ряд будет начинаться и заканчиваться числом «1». Внутренние члены вычисляются путём суммирования двух цифр над ним.
Запись в n строке и k столбце паскалевской фигуры обозначается (n k). Например, уникальная ненулевая запись в самой верхней строке (0 0) = 1. С помощью этого конструкция предыдущего абзаца может быть записана следующим образом, образуя формулу треугольника Паскаля (n k) = (n — 1 k-1) + (n — 1 k), для любого неотрицательного целого числа n и любого целого числа k от 0 до n включительно. Трёхмерная версия называется пирамидой или тетраэдром, а общие — симплексами.
Видео:Математика это не ИсламСкачать

История открытия
Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».
Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.
Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.
Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.
Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.
На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.
В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Отличительные черты
Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел. Обзор следует начать с простого — ряды:
- Сумма элементов одной строки в два раза больше суммы строки, предшествующей ей. Например, строка 0 (самая верхняя) имеет значение 1, строчка 1–2, а 2 имеет значение 4 и т. д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n .
- Принимая произведение элементов в каждой строке, последовательность продуктов можно связать с основанием натурального логарифма.
- В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
- Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11 n для строки n). Таким образом, в строке 2 ⟨1, 2, 1⟩ становится 11 2 , равно как ⟨1, 5, 10, 10, 5, 1⟩ в строке пять становится (после переноса) 161, 051, что составляет 11 5 . Это свойство объясняется установкой x = 10 в биномиальном разложении (x + 1) n и корректировкой значений в десятичной системе.
- Некоторые числа в треугольнике Паскаля соотносятся с числами в треугольнике Лозанича.
- Сумма квадратов элементов строки n равна среднему элементу строки 2 n. Например, 1 2 + 4 2 + 6 2 + 4 2 + 1 2 = 70.
- В любой строчке n, где n является чётным, средний член за вычетом члена в двух точках слева равен каталонскому числу (n / 2 + 1).
- В строчке р, где р представляет собой простое число, все члены в этой строке, за исключением 1s, являются кратными р.
- Чётность. Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму. Пусть x будет числом 1s в двоичном представлении. Тогда количество нечётных членов будет 2 х . Эти числа являются значениями в последовательности Гулда.
- Каждая запись в строке 2 n -1, n ≥ 0, является нечётной.
- Полярность. Когда элементы строки треугольника Паскаля складываются и вычитаются вместе последовательно, каждая строка со средним числом, означающим строки с нечётным числом целых чисел, даёт 0 в качестве результата.
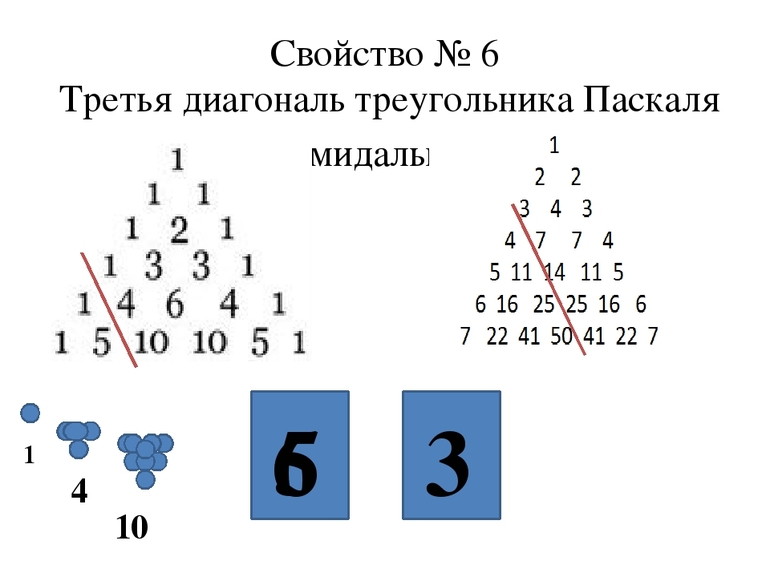
Диагонали треугольника содержат фигурные числа симплексов. Например:
- Идущие вдоль левого и правого краёв диагонали содержат только 1.
- Рядом с рёбрами диагонали содержат натуральные числа по порядку.
- Двигаясь внутрь, следующая пара содержит треугольные числа по порядку.
- Следующая пара — тетраэдрические, а следующая пара — числа пятиугольника.
Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.
Видео:✓ Бином Ньютона. Игра в слова. Числа сочетаний | Комбинаторика | Ботай со мной #057 | Борис ТрушинСкачать

Общие свойства
Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.
В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.
Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки — 0.
Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).
Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.
Видео:Числа сочетаний. Треугольник Паскаля | Ботай со мной #059 | Борис Трушин |Скачать

Секреты треугольника
Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.
Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.
Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.
Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.
Полномочия двойки
Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:
| 1 | ||||||||||||||
| 1 | + | 1 | = | 2 | ||||||||||
| 1 | + | 2 | + | 1 | = | 4 | ||||||||
| 1 | + | 3 | + | 3 | + | 1 | = | 8 | ||||||
| 1 | + | 4 | + | 6 | + | 4 | + | 1 | = | 16 | ||||
| 1 | + | 5 | + | 10 | + | 10 | + | 5 | + | 1 | = | 32 | ||
| 1 | + | 6 | + | 15 | + | 20 | + | 15 | + | 6 | + | 1 | = | 64 |
Суммирование строк показывает силы базы 2.
Силы одиннадцати
Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:
| 1 | = | 11° |
| 11 | = | 11¹ |
| 121 | = | 11² |
| 1331 | = | 11³ |
Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.
Совершенные квадраты
Если утверждать, что 4² — это 6 + 10 = 16, то можно найти идеальные квадраты натуральных чисел в столбце 2, суммируя число справа с числом ниже. Например:
- 2² → 1 + 3 = 4
- 3² → 3 + 6
- 4² → 6 + 10 = 16 и так далее.
Комбинаторные варианты
Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.
Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.
Видео:Бином Ньютона. Практическая часть. 10 класс.Скачать

Действия с биномами
Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).
В виде более удобной формулы этот процесс представлен в теореме бинома. Как известно, всё лучше разбирать на примерах. Итак — (2x – 3)³. Пусть x будет первым слагаемым, а y — вторым. Тогда x = 2x, y = –3, n = 3 и k — целые числа от 0 до n = 3, в этом случае k = . Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.
Как известно, комбинаторные числа взяты из треугольника, поэтому можно просто найти четвёртую строку и подставить в значения 1, 3, 3, 1 соответственно, используя соответствующие цифры Паскаля 1, 3, 3, 1. Последнее — необходимо завершить умножение и упрощение, в итоге должно получиться: 8 x³ — 36 x² + 54x — 27. С помощью этой теоремы можно расширить любой бином до любой степени, не тратя время на умножение.
Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.
Если спроектировать этот эксперимент с тремя испытаниями, с условием, что нужно узнать вероятность выпадения «решки», можно использовать функцию вероятности массы (pmf) для биномиального распределения, где n — это количество испытаний, а k — это число успехов. Предполагаемая вероятность удачи — 0,5 (р = 0,5). Самое время обратиться к треугольнику, используя комбинаторные числа: 1, 3, 3, 1. Вероятность получить ноль или три «решки» составляет 12,5%, в то время как переворот монеты один или два раза на сторону «орла» — 37,5%. Вот так математика может применяться в жизни.
Видео:3.2 Бинарные отношения | Роман Попков | ИТМОСкачать

Операции над множествами
Рассмотрим операции над множествами , которые позволяют из уже имеющихся множеств образовывать новые множества.
Для любых двух множеств и определены новые множества, называемые объединением, пересечением, разностью и симметрической разностью:
т.е. объединение и есть множество всех таких , что является элементом хотя бы одного из множеств ; пересечение и — множество всех таких , что — одновременно элемент и элемент ; разность — множество всех таких , что — элемент , но не элемент ; симметрическая разность — множество всех таких , что — элемент , но не элемент или — элемент , но не элемент .
Кроме того, фиксируя универсальное множество , мы можем определить дополнение множества следующим образом: . Итак, дополнение множества — это множество всех элементов универсального множества, не принадлежащих .
Полезно разобраться в том, как операции над множествами, введенные выше, соотносятся с логическими операциями. Пусть и , т.е. множество задано посредством характеристического предиката , а множество — посредством характеристического предиката .
Легко показать, что
Следующие процедуры получения новых множеств связаны с понятием подмножества. Говорят, что есть подмножество множества , если всякий элемент есть элемент . Для обозначения используют запись: . Говорят также, что содержится в или включено в , или включает (имеет место включение ). Считают, что пустое множество есть подмножество любого множества и, если фиксировано некоторое универсальное множество, каждое рассматриваемое множество есть его подмножество. Нетрудно проверить, что если и , то тогда и только тогда, когда высказывание тождественно истинно.
Сопоставляя определение подмножества и определение равенства множеств, мы видим, что множество равно множеству тогда и только тогда, когда есть подмножество и наоборот, т.е.
Формула (1.2) является основой для построения доказательств о равенстве множеств. Ее применение состоит в следующем. Чтобы доказать равенство двух множеств и , т.е. что , достаточно доказать два включения и «, т.е. доказать, что из предположения (для произвольного ) следует, что , и, наоборот, из предположения следует, что . Такой метод доказательства теоретико-множественных равенств называют методом двух включений. Примеры применения этого метода мы дадим позже.
Замечание. Равенство множеств и означает, что предикаты Р(х) и Q(x) эквивалентны, т.е. предикат Р(х) О Q<x) является тождественно истинным.
Видео:Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

Собственное подмножество и булеан множества
Если , но , то пишут и называют строгим подмножеством (или собственным подмножеством ) множества , а символ — символом строгого включения.
Для всякого множества может быть образовано множество всех подмножеств множества . Его называют булеаном множества и обозначают
Для булеана используют также обозначения и .
Пример. а. Булеан множества состоит из четырех множеств
б. Булеан состоит из всех возможных, конечных или бесконечных, подмножеств множества . Так, и , вообще для любого множество , множество
Для булеана мы можем рассматривать произвольные его подмножества. Таким подмножеством, например, будет Одноэлементное множество , где — произвольное подмножество . Подчеркнем, что единственным элементом множества является, в свою очередь, некоторое множество. Вообще же образование булеана открывает путь для построения множеств, элементами которых являются множества, элементами которых, в свою очередь, являются некоторые множества, и т.д. Так можно определить множества и т.д.
Видео:Математика для всех. Алексей Савватеев. Лекция 5.6. Бином НьютонаСкачать

Свойства операций над множествами
Введенные выше операции над множествами обладают следующими свойствами:
Каждое из написанных выше равенств, верное для любых входящих в них множеств, часто называют теоретико-множественным тождеством. Любое из них может быть доказано методом двух включений. Докажем этим методом тождество 19.
Пусть . Тогда, согласно определению симметрической разности, . Это означает, что или . Если , то и , то есть и при этом . Если же , то и , откуда и . Итак, в любом случае из следует и , то есть . Таким образом, доказано, что
Покажем обратное включение .
Пусть . Тогда и . Из следует, что или . Если , то с учетом имеем , и поэтому . Если же , то опять-таки в силу получаем, что и . Итак, или , то есть . Следовательно,
Оба включения имеют место, и тождество 19 доказано.
Метод двух включений является универсальным и наиболее часто применяемым методом доказательства теоретико-множественных тождеств. Помимо метода двух включений для доказательства теоретико-множественных тождеств могут быть использованы другие методы, например метод характеристических функций.
Кроме того, теоретико-множественные тождества можно доказывать, используя ранее доказанные тождества для преобразования левой части к правой или наоборот. Такой метод доказательства часто называют методом эквивалентных преобразований.
Докажем этим методом тождество 22, пользуясь тождествами 1-19. Преобразуем левую часть к правой:
🎦 Видео
Множества и операции над нимиСкачать

Геометрическая вероятность. С какой вероятностью можно составить треугольникСкачать

Теорема о биссектрисе угла треугольника | Осторожно, спойлер! | Борис Трушин |Скачать

Дискретная математика. Видео 1. Минимизация булевых функций.Скачать

Полином ЖегалкинаСкачать

Дискретная математика. Лекция 1: Множества и отношенияСкачать

Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Convex deformation of discrete sphericonСкачать