Треугольник серпинского история создания (7 видео)

Треугольник Серпинского и треугольник Паскаля

Содержание

Что это?
И что с того?
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА ПО ФРАКТАЛЬНОЙ ГЕОМЕТРИИ НА ТЕМУ «КОВЁР СЕРПИНСКОГО»
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Понятие о фракталах.
Понятие о фракталах.
Некоторые свойства.
Треугольник Серпинского
Некоторые свойства
Варианты
💡 Видео

Что это?

Треугольник Серпинского

Треугольник Серпинского — один из известнейших фракталов, его построение — одна из первых лабораторных работ на рекурсию по соответствующим дисциплинам во многих ВУЗах. Выглядит фрактал следующим образом:

Треугольник Паскаля

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси.

И что с того?

Есть в треугольнике Паскаля интересная особенность. Он отображает вышеупомянутый фрактал своими числами. Если долго всматриваться в ~~бездну, бездна начинает всматриваться в тебя~~ значения, то можно увидеть, что чётные и нечетные числа располагаются группами, ибо есть одно негласное всем известное правило: четное+нечетное=нечетное, четное+четное=четное, нечетное+нечетное=четное.

Что ж, меньше слов, больше дела. Сделаем вывод немного нагляднее. Людям, не интересующимся программной реализацией следующий абзац будет неинтересен.

Я взял старый алгоритм расчета-вывода треугольника Паскаля и преобразовал его таким образом, что вместо значения чисел выводится остаток от его деления на 2. Стало быть, четные теперь стали нулями, нечетные — единицами. Сам код прилагаю ниже

Для пущей наглядности я разукрасил вывод следующим способом: вывод программы перенаправляется в файл, откуда по завершению выполнения первой, перл своими регэкспами заменяет единицы на красные буквы О, нули — на синие. Код скрипта ниже:

Из исходника видно, что смотреть мы будем html. Почему? Из соображений простоты. Только дерево DOM неверное получается. Исправим это скриптом на BASH и автоматизируем всё вышеописанное:

Итак, мы компилируем исходник на плюсах, его вывод уходит в текстовичок, баш «эхает» в html на перезапись началом дерева DOM, после чего текстовичок берет перл-скрипт, переделывает его в разноцветную html-версию, дополняет htmlку, после чего любезный БАШ снова завершает формирование дерева. Запускаем, смотрим:

Подчеркнем и сравним с оригиналом

PROFIT

Видео:#237. Великое фрактальное подобие (feat. @vectozavr )Скачать

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА ПО ФРАКТАЛЬНОЙ ГЕОМЕТРИИ НА ТЕМУ «КОВЁР СЕРПИНСКОГО»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Что Такое Фракталы? Простое Объяснение!Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА НА ТЕМУ

Понятие о фракталах.

Основатель фрактальной геометрии.

Виды и основные свойства фракталов

О применении фракталов

Приложение 7 (Презентация)

Если люди отказываются верить

в простоту математики,

то это только потому, что они

не понимают всю сложность жизни.

Джон фон Нейман

Работа посвящена теме исследование фрактала: Ковер Серпинского.

Как известно, данный фрактал является одним из классических фракталов во фрактальной геометрии.

Основная цель данной работы заключается в исследовании фрактала под названием Ковер Серпинского.

Необходимость появления понятия фрактал появилась сравнительно недавно, а именно около 40 лет назад. Тогда геометрические модели различных природных конструкций традиционно строились на основе сравнительно простых геометрических фигур: прямых, многоугольников, окружностей, многогранников, сфер. Однако стало очевидно, что этот классический набор, достаточный для описания элементарных структур, становится плохо применим, для таких сложных объектов, как очертание береговых линий материков, поле скоростей в турбулентном потоке жидкости, разряд молнии в воздухе, пористые материалы, форма облаков, снежинки, пламя костра, контуры дерева и т.д. В связи с этим ученые стали вводить новые геометрические понятия. И одним из таких понятий стало понятие фрактала. Введено это понятие было французским математиком польского происхождения Бенуа Мандельбротом в1975 году. И хотя в математике похожие конструкции в той или иной форме появились давно, в физике ценность подобных идей была осознана лишь в 70 годы 20 столетия. Тогда немаловажную роль в распространении идей фрактальной геометрии сыграла книга Мандельброта «Фрактальная геометрия природы». Основой новой геометрии является идея самоподобия. Она выражает собой тот факт, что иерархический принцип организации фрактальных структур не претерпевает значительных изменений при рассмотрении их через микроскоп с различным увеличением. В результате эти структуры на малых масштабах выглядят в среднем также, как и на больших. Здесь определена разница между геометрией Евклида, имеющей дело исключительно с гладкими кривыми, и бесконечно изрезанными самоподобными фрактальными кривыми. Элементы кривых у Евклида всегда самоподобны, но тривиальным образом: все кривые являются локально прямыми, а прямая всегда самоподобна. Фрактальная же кривая, в идеале, на любых, даже самых маленьких масштабах не сводится к прямой и является в общем случае геометрически нерегулярной, хаотичной. Для нее, в частности, не существует и понятия касательной в точке, так как функции, описывающие эти кривые, являются в общем случае недифференцируемыми.

Возможно, что наиболее убедительным аргументом в пользу изучения фракталов является их бросающаяся в глаза красота.

Фракталы удивительным образом соединили логический подход и познание природных явлений.

Многие крупные достижения в области фрактальной геометрии стали возможны с появлением современных компьютеров. Компьютерные эксперименты позволили получить достаточно полное представление о разнообразных фракталах и причинах их возникновения. Часто теоретическое моделирование этих структур подчас даже опережало экспериментальные методы изучения реальных природных объектов сложной формы.

С развитием фрактальной геометрии, для многих стало очевидно, что формы евклидовой геометрии сильно проигрывают большинству природных объектов из-за отсутствия нерегулярности, беспорядка и непредсказуемости.

В настоящее время можно сказать, что фрактальная геометрия обширно известна и достаточно актуальна. Все потому, что язык фрактальной геометрии применим для всей науки современного мира в целом. Например, в медицине для построения модели кровеносной системы человека или рассмотрении сложных поверхностей клеточных мембран.

Понятие о фракталах.

Фракталы вокруг нас повсюду, и в очертаниях гор, и в извилистой линии морского берега. Некоторые из фракталов непрерывно меняются, подобно движущимся облакам или мерцающему пламени, в то время как другие, подобно деревьям или нашим сосудистым системам, сохраняют структуру, приобретенную в процессе эволюции.
Х. О. Пайген и П. Х. Рихтер.

Геометрия, которую мы изучаем в школе и которой пользуемся в повседневной жизни, как говорилось ранее, восходит к Эвклиду (примерно 300 лет до нашей эры). Треугольники, квадраты, круги, параллелограммы, параллелепипеды, пирамиды, шары, призмы — типичные объекты, рассматриваемые классической геометрией. Предметы, созданные руками человека, обычно включают эти фигуры или их фрагменты. Однако в природе они встречаются не так уж часто. Действительно, похожи ли, например, лесные красавицы ели на какой-либо из перечисленных предметов или их комбинацию? Легко заметить, что в отличие от форм Эвклида природные объекты не обладают гладкостью, их края изломаны, зазубрены, поверхности шероховаты, изъедены трещинами, ходами и отверстиями.

«Почему геометрию часто называют холодной и сухой? Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака — это не сферы, горы — не конусы, линии берега — это не окружности, и кора не является гладкой, и молния не распространяется по прямой. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности» , — этими словами начинается «Фрактальная геометрия природы», написанная Бенуа Мандельбротом. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов . Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта « The Fractal Geometry of Nature» . В его работах использованы научные результаты других ученых, работавших в период 1875 -1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.

Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.

Фракталы — это геометрические объекты с удивительными свойствами: любая часть фрактала содержит его уменьшенное изображение. То есть, сколько фрактал не увеличивай, из любой его части на вас будет смотреть его маленькая копия.

Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому» . Внутренние свойства фракталов удобно описывать числовой характеристикой, полу чившей название фрактальной размерности. Проведём несложный эксперимент. Возьмём лист чистой миллиметровой бумаги и начер тим на нём произвольный прямолинейный отрезок. Подсчитаем количество кле ток с длиной стороны 1 см и количество кле точек с длиной стороны 1 мм, через которые проходит этот отрезок. Во сколько раз одно число больше другого? Если эксперимент про водить аккуратно, то покрывающих отрезок миллиметровых клеток окажется в десять раз больше, чем сантиметровых.

Геометрия в природе не ограничивается такими простыми фигурами, как линия, круг, коническое сечение, многоугольник, сфера, квадратичная поверхность, а также их комбинациями. К примеру, что может быть красивее утверждения о том, что планеты в нашей солнечной системе движутся вокруг солнца по эллиптическим орбитам?

Однако многие природные системы настолько сложны и нерегулярны, что использование только знакомых объектов классической геометрии для их моделирования представляется безнадежным. Как к примеру, построить модель горного хребта или кроны дерева в терминах геометрии? Как описать то многообразие биологических конфигураций, которое мы наблюдаем в мире растений и животных? Представьте себе всю сложность системы кровообращения, состоящей из множества капилляров и сосудов и доставляющей кровь к каждой клеточке человеческого тела. Представьте, как хитроумно устроены легкие и почки, напоминающие по структуре деревья с ветвистой кроной.

Столь же сложной и нерегулярной может быть и динамика реальных природных систем. Как подступиться к моделированию каскадных водопадов или турбулентных процессов, определяющих погоду?

Фракталы и математический хаос — подходящие средства для исследования поставленных вопросов. Термин фрактал относится к некоторой статичной геометрической конфигурации, такой как мгновенный снимок водопада. Хаос — термин динамики, используемый для описания явлений, подобных турбулентному поведению погоды. Нередко то, что мы наблюдаем в природе, интригует нас бесконечным повторением одного и того же узора, увеличенного или уменьшенного во сколько угодно раз. Например, у дерева есть ветви. На этих ветвях есть ветки поменьше и т.д. Теоретически, элемент «разветвление» повторяется бесконечно много раз, становясь все меньше и меньше. То же самое можно заметить, разглядывая фотографию горного рельефа. Попробуйте немного приблизить изображение горной гряды — вы снова увидите горы. Так проявляется характерное для фракталов свойство самоподобия.

Во многих работах по фракталам самоподобие используется в качестве определяющего свойства. Следуя Бенуа Мадельброту, мы принимаем точку зрения, согласно которой фракталы должны определяться в терминах фрактальной (дробной) размерности. Отсюда и происхождение слова фрактал (от лат. fractus — дробный).

Понятие дробной размерности представляет собой сложную концепцию, которая излагается в несколько этапов. Прямая — это одномерный объект, а плоскость — двумерный. Если хорошенько перекрутив прямую и плоскость, можно повысить размерность полученной конфигурации; при этом новая размерность обычно будет дробной в некотором смысле, который нам предстоит уточнить. Связь дробной размерности и самоподобия состоит в том, что с помощью самоподобия можно сконструировать множество дробной размерности наиболее простым образом. Даже в случае гораздо более сложных фракталов, таких как граница множества Мандельброта, когда чистое самоподобие отсутствует, имеется почти полное повторение базовой формы во все более и более уменьшенном виде.

Основатель фрактальной геометрии.

Математики пренебрегли вызовом и

предпочли бежать от природы путём изобретения

всевозможных теорий, которые никак не

объясняют того, что мы видим или ощущаем.

Бенуа Мандельброт (фр. Benoit Mandelbrot; род. 20 ноября 1924, Варшава) — французский математик.

Основатель и ведущий исследователь в области фрактальной геометрии. Лауреат премии Вольфа по физике (1993).

Бенуа Мaндельброт родился в Варшаве в 1924 году в семье литовских евреев. Но уже в 1936 году семья Бенуа Мандельброта эмигрировала во Францию, в Париж. В Париже он попал под влияние своего дяди Шолема Мандельбройта, известного парижского математика, члена группы математиков, известной под общим псевдонимом «Николя Бурбаки».

После начала войны Мандельброты бежали на свободный от оккупации юг Франции, в городок Тюль. Там Бенуа Мандельброт пошел в школу, но вскоре потерял интерес к учебе. Поэтому к шестнадцати годам он еле знал алфавит и таблицу умножения до пяти.

Но у Бенуа Мандельброта открылся необычный математический дар, который позволил ему сразу после войны стать студентом Сорбонны. Оказалось, что у Бенуа великолепное пространственное воображение. Он даже алгебраические задачи решал геометрическим способом. Оригинальность его решений позволила Бенуа Мандельброту поступить в университет.

Окончив университет, Бенуа Мандельброт сначала стал «чистым математиком». Он получил докторскую степень.

В 1958 он переехал в США, где приступил к работе в научно-исследовательском центре IBM в Йорктауне, поскольку IBM в то время занималась как раз интересными Бенуа Мандельброту областями математики.

Работая в IBM, Бенуа Мандельброт ушел далеко в сторону от чисто прикладных проблем компании. Он работал в области лингвистики, теории игр, экономики, аэронавтики, географии, физиологии, астрономии, физики. Ему нравилось именно переключаться с одной темы на другую, изучать различные направления.

Исследуя экономику, Бенуа Мандельброт обнаружил, что произвольные внешне колебания цены могут следовать скрытому математическому порядку во времени, который не описывается стандартными кривыми.

Бенуа Мандельброт занялся изучением статистики цен на хлопок за большой период времени (более ста лет). Колебания цен в течение дня казались случайными, но Мандельброт смог выяснить тенденцию их изменения. Он проследил симметрию в длительных колебаниях цены и колебаниях кратковременных. Это открытие оказалось неожиданностью для экономистов.

По сути, Бенуа Мандельброт применил для решения этой проблемы зачатки своего рекурсивного (фрактального) метода.

Немного о надкусывании

Представьте себе, что вы выдрессировали крыс — они научились отгрызать ровно половину наличного сыра. Если вы будете выпускать их на сыр не всем гуртом, а по одной, то каждая следующая откусит половину от того, что осталось, а оставшаяся часть будет уменьшаться и уменьшаться с каждой надкусившей сыр крысой. Но если вы обзавелись бесконечным количеством крыс, то в конце концов (смешно звучит по отношению к бесконечности, зато честно) от сыра ничего не останется. Действительно, первая ест одну вторую сыра, вторая — одну четвёртую, т.е. половину от половины, третья — одну восьмую, т.е. половину от половины от половины. Всё съеденное считается так:

а значит, крысы к концу бесконечности съедят ВЕСЬ сыр, что вы им выдали.
А вот если вы будете натаскивать грызунов на выкус одной третьей от всего наличного, всё будет несколько хитрее. Первая съест одну третью. Но вторая — не одну девятую. Почему?
Объяснение довольно просто. После того, как съела свою долю первая крыса, осталось 2/3 сыра, а значит, вторая крыса съест 1/3 от 2/3, т.е. 2/9. Третья, как можно посчитать, съест 1/3 от 7/9, т.е. 7/27, четвёртая — 1/3 от 20/27, т.е. 20/81… поняли принцип?
В конечном счёте от сыра всё равно ничего не останется.
Теперь представьте, что вы разделили сыр пополам, и одну из частей (половин, но об этом крысы не знают) объявили запретной — например, посыпали ядом, — а от второй разрешили крысам откусывать половину. Как вы догадались, от разрешённой половины ничего не останется, а запретная останется вся.
Особо любопытна такая дрессировка крыс, при которой никакую половину сыра вы ядом не посыпаете, но что-то вам достаётся всё равно (это чтобы вы не отравились). Для этого, например, можно выучить крыс откусывать 2 n-1 /5 n от стартового количества сыра. По окончании бесконечного обеда крысы оставят вам 1/3 сыра — это считается следующим образом:

В нашем случае от пяти надо отнять два, выйдет три, а если один поделить на три, выйдет как раз одна третья.
Если вы по какой-то причине пропустили эту цифирь, значит , вернётесь к ней через пару минут. Или лет. Или по прочтении поста. Или по вторичном прочтении. Или в следующей жизни. В конце концов, человек только тогда достигает совершенства, когда в одной из прошлых жизней он был математиком.
Но даже если вы вернётесь к цифири только в следующей жизни, вы неизбежно запомните вот это вот: 1/(b-a). Пригодится!

Немного о раскалывании

Теперь другая, не менее идиотская жизненная задача. Представьте, что вы решили повесить на стену тарелку. В доме нет ни клея, ни скотча — только гвозди. Вы пытаетесь прибить тарелку гвоздём, и она, разумеется, раскалывается на некоторое число кусочков. Кроме того, в месте, по которому вы ударили гвоздём, выкрошилось напрочь некоторое количество тарелки.
Но вы упорны. О, да, вы упорны! И вы пытаетесь прибить к стенке каждый осколок тарелки. Может быть, берёте гвозди поменьше.
Разумеется, каждый из осколков крошится на свои, более мелкие осколки, а в серединках бывших осколков что-то безвозвратно выкрашивается. Ну и пусть.
Если быть бесконечно упорным и пытаться прибить осколки, получившиеся в результате бесконечного числа попыток, не останется ни кусочка тарелки, который не был бы проткнут гвоздём и не нёс бы выкрошенной дырочки.
Но, как вы уже можете догадаться, вовсе не обязательно, что от тарелки ничего не останется. Всё зависит от того, как вы дрессировали ваши гвозди. Если они выкрашивают не слишком много тарелки, то общая площадь выкрошенного может быть и меньше, чем площадь оставшихся осколков. А может и больше — главное, что она будет меньше площади всей бывшей тарелки.
Почему-то очень хочется написать, что тарелка была выточена из гранита науки, но я этого не сделаю.
Польский учёный Вацлав Серпинский (1882-1969) не дрессировал крыс и не бил тарелки. Он был математиком. И самая известная его сюрреалистски-математическая акция заключалась в резьбе по салфеткам и коврам.
Две наиболее известные фигуры, придуманные Серпинским — «салфет ка» (треугольник, из которого последовательно вырезаются треугольники всё меньшего размера, каждый площадью вчетверо меньше предыдущего) и ковёр (квадрат с вырезкой из квадратиков, каждый квадратик площадью вдевятеро меньше предыдущего).

Площадь получившейся после бесконечного числа вырезок фигуры — как салфетки, так и ковра — равна нулю. Да и не совсем фигуры это.
Тут следует остановиться и сформулировать отличие фигуры от линии.
С одной стороны, фигура, вроде бы, имеет площадь, а линия её не имеет. Ещё Евклид писал, что линия это длина без ширины, а какая же площадь без ширины? Никакого раздолья!
Но математиков это не удовлетворило, и они решили уточнить, что значит «без ширины». И договорились: если на чём-то выбрать точку и описать вокруг этой точки круг без границы (математики называют его деревенским словом «окрестность»), а потом начать его уменьшать, то если рано или поздно вся окрестность попадёт внутрь этого чего-то, то, значит, это была фигура. А если в окрестности всегда будут «чужие» точки, значит, это что-то было линия.

Конечно, линия на картинке — никакая не линия. Линию вообще нельзя нарисовать, след от карандаша или курсора всегда имеет ширину. Линию можно только ОБОЗНАЧИТЬ. А такая вот, нарисованная, рано или поздно поглотит уменьшающуюся окрестность. На то и знак. Некоторые знаки крупнее означаемых ими объектов.
Так вот. Поскольку ковры и салфетки Серпинского раскалываются, как наша тарелка, всё мельче и мельче, и в центре каждого осколка есть «выкрошенная» зона, при бесконечном выкрашивании и раскалывании в окрестность любой сохранившейся точки фигуры Серпинского попадут «пустоты». Значит, это линия.
Ну да, всё как положено: это хитрозапутанная линия, и площадь линии равна нулю.
Но если вырезать из ковра квадратики чуть меньшей площади, может выйти и так, что оставшаяся часть будет иметь площадь больше, чем ноль. Скажем, если выкинуть сперва одну двадцать пятую (квадратик со стороной, в пять раз меньше исходного), потом восемь квадратиков, в двадцать пять раз меньше вырезанного на первом шаге, потом — шестьдесят четыре меньших ещё в пять раз… словом, вспомните то, что я предлагал вам запомнить, и убедитесь, что вырежется из такого ковра всего 1/17 часть. А 16/17 останется. Но в окрестности любой точки того, что останется, всё равно будут дырки. Такая вот линия с площадью.
А ведь можно вырезать и ещё меньшие квадратики! Да и не обязательно квадратики, было бы чётко задано правило, по которому мы вырезаем дырки и раскалываем то, что осталось, на новые кусочки. В каждом кусочке должна появиться дырка — вот и весь секрет изготовления линий из фигур. А от размера дырок зависит, будут ли линии иметь площадь, или останутся «длиной без ширины».
Фигуры Серпинского — пожалуй, самые простые и самые красивые из известных мне фракталов.

Мне сразу показалось удивительным, что нечто, имеющее площадь, может всё, как есть, быть границей между самим собой и окружающей средой. Слишком уж это напоминает устройство живого организма. Вот вдумайтесь: то, что внутри кишок — это относится к организму или нет? А то, что в межклеточных щелях? А то, что в толще цитоплазмы, а не на мембранах?
А в последнее время я всё больше и больше задумываюсь над тем, что и человеческая психика устроена сходным образом. Она — вся, всей своей толщей — пограничное явление.

Вацлав Франциск Серпинский , в другой транскрипции — Серпиньский (польск. Wacław Franciszek Sierpiński); (14 марта 1882, Варшава, Польша — 21 октября 1969, Варшава) — выдающийся польский математик. Известен своими трудами по теории множеств, аксиоме выбора, континуум-гипотезе, теории чисел, теории функций, а также топологии. Автор 724 статей и 50 книг.

Вацлав Франциск родился в семье врача Константина Серпинского.
В 1900 году поступил на физико-математический факультет Варшавского университета. В 1904 году после окончания университета, получив степень кандидата наук и золотую медаль за работу в области теории чисел, он был назначен преподавателем математики и физики в женской гимназии Варшавы.
Когда в 1905 году школы были закрыты из-за забастовки, Серпинский решил поехать в Краков для подготовки к защите докторской диссертации. В Ягеллонском университете он посещал лекции Заремба по математике, посещал лекции по астрономии и философии. В 1906 году он получил степень доктора философии. В январе 1908 года он стал членом Варшавского научного общества, а в июле получил докторскую степень и начал читать лекции по теории множеств в Львовском университете. В сентябре 1910 года он был назначен профессором. За время преподавания в университете Львова (1908—1914), он опубликовал три книги и большое количество статей.
Первая мировая война застала его с семьёй в Беларусии и он был сослан в Вятку: у В.Серпинского было немецкое подданство. Благодаря усилиям математиков Д. Ф. Егорова и Н. Н. Лузина ему позволено жить в Москве, где он работал вместе с Лузиным, участвовал в Лузитании. Летом 1918 года Серпинский начал читать лекции во Львове, но с осени 1918 года стал преподавать в Варшавском университете, где в апреле 1919 года был назначен профессором. В 1921 году он был избран в Польскую академию и стал деканом факультета Варшавского университета. В 1928 году он стал вице-президентом Общества науки и литературы Варшавы (с ноября 1931 года — президент) и, в том же году был избран председателем Польского математического общества. Он участвовал в работе на международных математических конгрессах в Торонто (1924), Болонье (1928), Цюрихе (1932) и Осло (1936).
Один из участников международной поддержки против политической травли в «деле Лузина» (1936).
В октябре 1944 года вместе с домом погибла его ценная библиотека. После освобождения из нацистского лагеря в феврале 1945 года он приехал в Краков, читал лекции в Ягеллонском университете, а осенью вернулся в Варшаву. В 1960 году вышел на пенсию, но продолжал вести семинар по теории чисел в Польской академии наук до 1967 года.
Он был членом Польской Академии наук (с 1952) и её вице-президентом (до 1957).
Он был удостоен почётных степеней университетов Львова (1929), Святого Марка в Лиме (1930), Амстердама (1931), Софии (1939), Праги (1947), Вроцлава (1947), Лакхнау (1949), Московского университета(1967).
Он был членом Географического общества Лимы (1931), Королевского научного общества Льежа (1934), Болгарской академии наук (1936), Национальной академии Лимы (1939), Королевского общества наук в Неаполе (1939), Академии деи Линчеи в Риме (1947), Немецкой академии наук (1950), Американской академии искусств и наук (1959), Парижской академии (1960), Королевской голландской академии (1961), Международной академии философии науки в Брюсселе (1961), Лондонского математического общества (1964), Румынской академии (1965) и Папской академии наук (1967).
Конечно, нужна определенная сила воли, чтобы одолеть такой монолитный текст из Википедии. Поэтому сделаю один небольшой акцент, касающийся Лузина и Лузитании (в связи с Серпинским, разумеется). А кто захочет, сможет потом уже сам нагуглить.
В 1915 году в Москве оказался польский математик Вацлав Серпинский, интернированный из-за своего немецкого гражданства. Д. Ф. Егоров и Н. Н. Лузин помогли ему выхлопотать разрешение на свободное проживание в Москве. В. Серпинский активно участвовал в создании Московской математической школы. Тесные контакты школ Лузина и Серпинского продолжались до середины 30-х годов. Первыми участниками Лузитании стали П. С. Александров, М. Я. Суслин, Д. Е. Меньшов, А. Я. Хинчин; несколько позже появились В. Н. Вениаминов, П. С. Урысон, А. Н. Колмогоров, В. В. Немыцкий, Н. К. Бари, С. С. Ковнер, В. И. Гливенко, Л. А. Люстерник, Л. Г. Шнирельман. Через несколько лет (1923—1924 годы) прибавилось третье поколение — П. С. Новиков, Л. В. Келдыш, Е. А. Селивановский. Одним последних к школе Лузина присоединился А. А. Ляпунов (1932 год). В это время Лузитании уже практически не было.

Мой «персональный» интерес к Серпинскому,
конечно же, связан в первую очередь с треугольником и ковром Серпинского.

Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Серпинским в 1915 году. Также известен как «решётка» или «салфетка» Серпинского.

Построение треугольника Серпинского:

Пусть начальное множество S ₀ — равносторонний треугольник вместе с областью, которую он замыкает. Разобьем S ₀ на четыре меньшие треугольные области, соединив отрезками середины сторон исходного треугольника. Удалим внутренность маленькой центральной треугольной области. Назовем оставшееся множество S ₁ (рис.). Затем повторим процесс для каждого из трех оставшихся маленьких треугольников и получим следующее приближение S ₂ . Продолжая таким образом, получим после-довательность вложенных множеств S _n , чье пересечение образует ковер S .

Из построения видно, что весь ковер представляет собой объединение N = 3 существенно не пересекающихся уменьшенных в два раза копий; коэффициент подобия r = Ѕ (как по горизонтали, так и по вертикали). Следовательно, S — самоподобный фрактал с размерностью:

Сам треугольник:

Очевидно, что суммарная площадь частей, выкинутых при построении, в точности равна площади исходного треугольника. На первом шаге мы выбросили ј часть площади. На следующем шаге мы выбросили три треугольника, причем площадь каждого равна ј 2 площади исходного. Рассуждая таким образом, мы убеждаемся, что полная доля выкинутой площади составила:

Эта сумма равна 1

Следовательно, мы можем утверждать, что оставшееся множество S , то есть ковер, имеет площадь меры нуль. Это выделяет множество S в разряд «совершенного», в том смысле, что оно разбивает свое дополнение на бесконечное число треугольных областей, обладая при этом нулевой толщиной.

Треугольник Серпинского можно получить по следующему алгоритму:

Взять три точки на плоскости, и нарисовать треугольник.

Случайно выбрать любую точку внутри треугольника, и продвинуться на половину расстояния от этой точки к любой из трех вершин треугольника.

Отметить текущую позицию.

Повторить с шага 2.

Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться «в обратном направлении»: взять изначально «пустой» треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т. д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут.

Построение треугольника Серпинского «в обратном направлении»

Следующий способ получить треугольник Серпинского еще больше похож на обычную схему построения геометрических фракталов с помощью замены частей очередной итерации на масштабированный фрагмент. Здесь на каждом шаге составляющие ломаную отрезки заменяются на ломаную из трех звеньев (она сама получается в первой итерации). Откладывать эту ломаную нужно попеременно то вправо, то влево. Видно, что уже восьмая итерация очень близка к фракталу, и чем дальше, тем ближе будет подбираться к нему линия.

Но и на этом не всё. Оказывается, треугольник Серпинского получается в результате одной из разновидностей случайного блуждания точки на плоскости. Этот способ называется «игрой Хаос»

С его помощью можно построить и некоторые другие фракталы.

Некоторые свойства.

1.Треугольник Серпинского замкнут.
2. Треугольник Серпинского имеет топологическую размерность 1.
3. Треугольник Серпинского имеет промежуточную (то есть, нецелую) Хаусдорфову размерность `ln3/(ln2)

1,585`.
— В частности, треугольник Серпинского имеет нулевую меру Лебега.

Треугольник Серпинского имеет нулевую площадь. То есть, если отталкиваться от построения первым способом, из треугольника «вынули» всю внутренность: после каждой итерации площадь того, что остается, умножается на 3/4, то есть становится всё меньше и стремится к 0.

Существует так же неожиданная связь треугольника Серпинского с комбинаторикой: если в треугольнике Паскаля с 2 n строками покрасить все четные числа одним цветом, а нечетные — другим, образуется треугольник Серпинского в некотором приближении.

Интересные факты
Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные — в белый, то образуется треугольник Серпинского.
Образования, похожие на треугольник Серпинского, возникают в игре Жизнь из длинной вертикальной линии.

Ковёр Серпинского (квадрат Серпинского) — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Вацлавом Серпинским в 1915 году.

Построение ковра Серпинского получается из квадрата последовательным выре занием серединных квадратов. А именно, разделим дан ный квадрат на девять равных квадратов и серединный квадрат вырежем. Получим квадрат с дыркой. Для оставшихся восьми квадратов повторим указанную процедуру. Разделим каждый из них на девять равных квадратов и серединные квадраты вырежем. Повторяя эту процедуру, будем получать все более дыря вую фигуру. То, что остается после всех выреза ний, и будет искомым ковром Серпинского.

Поскольку вырезаемые квадраты распо лагаются все более часто, в результате на ковре Серпин ского не будет ни одного, даже самого маленького, квад рата без дырки.

Вычислим площадь ковра Серпинского, считая исходный квадрат единичным. Для этого достаточно вычислить п лощадь вырезаемых квадратов. На первом шаге выреза ется квадрат площади . На втором шаге вырезается во семь квадратов, каждый из которых имеет площадь .

На каждом следующем шаге число вырезаемых квадратов увеличивается в восемь раз, а площадь каждого из них уменьшается в девять раз. Таким образом, общая площадь вырезаемых квадратов представляет собой сумму геометрической прогрессий с начальным членом и знаменателем . По формуле суммы геометрической про грессии находим, что это число равно единице, т. е. пло щадь ковра Серпинского равна нулю.

Возьмем теперь квадрат площадью, равной двум, и вы режем из него квадрат с тем же центром площадью . Оставшуюся часть представим в виде восьми прямоуголь ников и в каждом из них вырежем квадрат с тем же цент ром площади . Таким образом, суммарная площадь маленьких квадратов будет равна . Повторяя эту процедуру, будем получать все более дырявую фигуру, которую также называют ковром Серпинского.

Также как и раньше, в этом ковре Серпинского не бу дет ни одного, даже самого маленького, квадрата без дырки . Однако, в отличие от обычного ковра Серпинского его площадь отлична от нуля. Действительно, площадь вырезаемых квадратов представляет собой сумму геометрической прогрессии с начальным членом и знамена телем , т. е. равна 1. Поэтому площадь оставшейся час ти равна единице.

Ковер Серпинского является двумерным аналогом функции Кантора .

Пусть Т – заданный правильный треугольник, А, В, С – его вершины: левая, верхняя и правая. Соединяя середины сторон треугольника Т, получим четыре новых правильных треугольника, три из которых – Т ₀ , Т ₁ , Т ₂ , содержат вершины А, В, С, расположенные параллельно Т, и четвертый треугольник U находится в центре треугольника Т; исключаем внутреннюю область треугольника U.

Произведем над каждым треугольником Т ₀ , Т ₁ , Т ₂ те же операции как и для треугольника Т: получим девять треугольников, расположенных параллельно треугольнику Т. На n-ом шаге имеем ; – новые треугольники. На рис. 7 приведен ковер Серпинского при .

Также построим прямоугольный ковер Серпинского. Берем квадрат со стороной, равной единице. На первом шаге делим его на 9 равных квадратов (со стороной 1/3), и все внутренние точки центрального квадрата удаляем (на рис. 8 эта часть выделена черным цветом). На втором шаге также поступаем с оставшимися 8 квадратами, причем возникают уже 64 квадрата (со стороной 1/9). Далее процесс повторяем на всё более и более мелких масштабах. Нетрудно найти, что суммарная площадь выброшенных квадратов

Оставшееся множество точек называется ковром Серпинского.

Как видно из приведенного построения, достаточно задать алгоритм одного шага преобразования, чтобы восстановить структуру фрактала на любых масштабах.

Примерно также получаются все остальные геометрические фракталы: вы берете какую-то фигуру и начинаете применять к ней, а потом к ее частям, определенное геометрическое построение достаточно много раз.

Отметим, что до сих пор рассматривалось построение фрактала с помощью какого-либо детерминированного алгоритма, однако может использоваться и вероятностный алгоритм. При этом свойство самоподобия у таких фракталов сохраняется «в среднем», т.е. после серии реализаций или серии масштабных преобразований.

Рассмотрим общий метод получения аналогичных отображений. В отличие от рассмотренных ранее нелинейных точечных отображений рассмотрим теперь системы линейных функций (отображений), задающих аффинные преобразования плоскости.

Каждое из преобразований системы можно записать в виде ,

Здесь матрица А осуществляет масштабирование исходного множества, а вектор b – сдвиг. Отображения должны быть сжимающими: .

Систему функций получим, рассматривая совместно набор п отображений Т = < >.

Алгоритм действия отображения Т состоит в следующем. Зададим некоторое компактное начальное множество точек Е ₀ на плоскости. Первое применение Т к этому множеству (т.е. первая итерация) дает множество

т. е. каждое из отображений должно быть применено к исходному множеству, а затем требуется объединить получившиеся множества. Следующие итерации можно записать в следующем виде:

Совокупность отображений называется системой итерированных функций (СИФ), описываемая согласно приведенной итерационной схеме

В качестве примера рассмотрим систему из отображений для салфетки Серпинского (Е ₀ – треугольник с вершинами (0,0), (1,0), (1/2, ),

Каждое из этих отображений – сжимающее, со степенью сжатия s = 1/4.

Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

Треугольник Серпинского

Для просмотра анимации необходимо включить JavaScript.

Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. На рисунке показаны первые три шага, а на флэш-демонстрации вы можете потренироваться и получить шаги вплоть до десятого.

Суть «игры» такова. На плоскости зафиксирован правильный треугольник A₁A₂A₃. Отмечают любую начальную точку B₀. Затем случайным образом выбирают одну из трех вершин треугольника и отмечают точку B₁ — середину отрезка с концами в этой вершине и в B₀ (на рисунке справа случайно выбралась вершина A₁). То же самое повторяют с точкой B₁, чтобы получить B₂. Потом получают точки B₃, B₄, и т. д. Важно, чтобы точка «прыгала» случайным образом, то есть чтобы каждый раз вершина треугольника выбиралась случайно, независимо от того, что было выбрано в предыдущие шаги. Удивительно, что если отмечать точки из последовательности B_i, то вскоре начнет проступать треугольник Серпинского. Ниже изображено, что получается, когда отмечено 100, 500 и 2500 точек.

Некоторые свойства

Фрактальная размерность log₂3 ≈ 1,584962. . Треугольник Серпинского состоит из трех копий самого себя, каждая в два раза меньше. Взаимное расположение их таково, что если уменьшить клеточки сетки в два раза, то число квадратиков, пересекающихся с фракталом, утроится. То есть N(δ/2) = 3N(δ). Если сначала размер клеток был 1, а с фракталом пересекалось N₀ из них (N(1) = N₀), то N(1/2) = 3N₀, N(1/4) = 3 2 N₀, . N(1/2 k ) = 3 k N₀. Отсюда получается, что N(δ) пропорционально , и по определению фрактальной размерности она равна как раз log₂3.
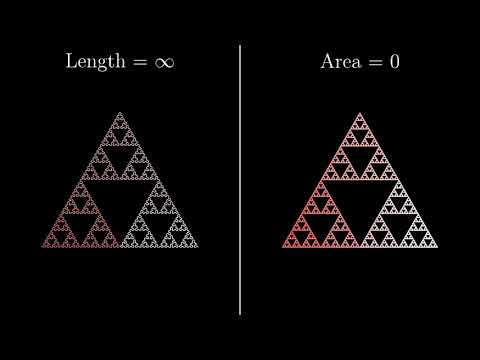
Треугольник Серпинского имеет нулевую площадь. Это означает, что в фрактал не влезет ни один, даже очень маленький, кружок. То есть, если отталкиваться от построения первым способом, из треугольника «вынули» всю внутренность: после каждой итерации площадь того, что остается, умножается на 3/4, то есть становится всё меньше и стремится к 0. Это не строгое доказательство, но другие способы построения могут только усилить уверенность, что это свойство всё-таки верно.
Неожиданная связь с комбинаторикой. Если в треугольнике Паскаля с 2 n строками покрасить все четные числа белым, а нечетные — черным, то видимые числа образуют треугольник Серпинского (в некотором приближении).

Варианты

Ковер (квадрат, салфетка) Серпинского. Квадратная версия была описана Вацлавом Серпинским в 1916 году. Ему удалось доказать, что любая кривая, которую можно нарисовать на плоскости без самопересечений, гомеоморфна какому-то подмножеству этого дырявого квадрата. Как и треугольник, квадрат можно получить из разных конструкций. Справа изображен классический способ: разделение квадрата на 9 частей и выбрасывание центральной части. Затем то же повторяется для оставшихся 8 квадратов, и т. д.

Как и у треугольника, у квадрата нулевая площадь. Фрактальная размерность ковра Серпинского равна log₃8, вычисляется аналогично размерности треугольника.

Пирамида Серпинского. Один из трехмерных аналогов треугольника Серпинского. Строится аналогично с учетом трехмерности происходящего: 5 копий начальной пирамиды, сжатой в два раза, составляют первую итерацию, ее 5 копий составят вторую итерацию, и т. д. Фрактальная размерность равна log₂5. У фигуры нулевой объем (на каждом шаге половина объема выбрасывается), но при этом площадь поверхности сохраняется от итерации к итерации, и у фрактала она такая же, как и у начальной пирамиды.

Губка Менгера. Обобщение ковра Серпинского в трехмерное пространство. Чтобы построить губку, нужно бесконечное повторение процедуры: каждый из кубиков, из которых состоит итерация, делится на 27 втрое меньших кубиков, из которых выбрасывают центральный и его 6 соседей. То есть каждый кубик порождает 20 новых, в три раза меньших. Поэтому фрактальная размерность равна log₃20. Этот фрактал является универсальной кривой: любая кривая в трехмерном пространстве гомеоморфна некоторому подмножеству губки. У губки нулевой объем (так как на каждом шаге он умножается на 20/27), но при этом бесконечно большая площадь.