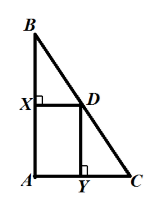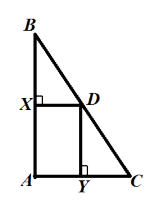Треугольник с 4 точками

Вы будете перенаправлены на Автор24

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Видео:Виды треугольниковСкачать

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

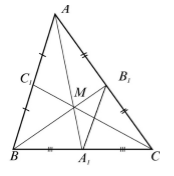
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

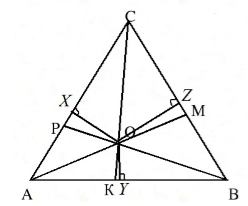
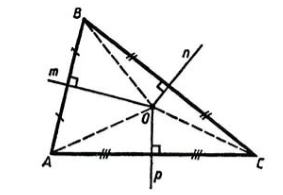
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

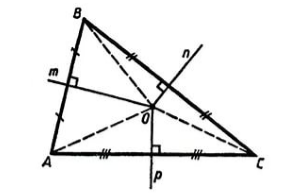
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Видео:четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

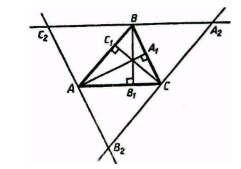
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2022

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Тема: «четыре замечательные точки треугольника»

ТЕМА: «ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА»

Свойства биссектрисы угла

Все точки биссектрисы угла равноудалены от сторон этого угла.

Свойства серединного перпендикуляра к отрезку

Все точки серединного перпендикуляра к отрезку равноудалены от концов этого отрезка.

Четыре замечательные точки треугольника

1) Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины;

2) Биссектрисы треугольника пересекаются в одной точке;

3) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке;

4) Высоты треугольника (или их продолжения) пересекаются в одной точке.

Найдите соответствующие точки, построив указанные элементы треугольника:

1) 2)

3) 4)

Пример 1. По данным рисунка найдите площадь треугольника BOQ, если QM = 9, BT = 12.

1) QM, BT – медианы ⇒ QO : OM = BO : OT = 2 : 1 (по свойству медиан треугольника);

2) QO : OM = 2 : 1, QM = 9 ⇒ QO = 2OM, QM = 3OM ⇒

OM = 9 : 3 = 3, QO = 9 – 3 = 6;

3) BO : OT = 2 : 1, BT = 12 ⇒ BO = 2OT, BT = 3OT ⇒

OT = 12 : 3 = 4, BO = 12 – 4 = 8;

4) QM⊥BT ⇒ ΔBOQ – прямоугольный ⇒ SBOQ = (по формуле площади прямоугольного треугольника).

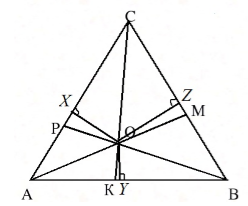
Пример 2. По данным рисунка найдите угол FNO, если угол MKN = 66°.

1) Продолжим NO до пересечения со стороной КМ. КМ∩NO = Р;

2) О – точка пересечения высот ⇒ NP – высота ΔKMN ⇒ NP⊥КМ ⇒ ΔKPM – прямоугольный;

3) ΔKPM – прямоугольный ⇒ ∠РKN + ∠КNР = 90° (по свойству острых углов прямоугольного треугольника);

∠КNР = 90° — ∠РKN = 90° — 66° = 24°;

Пример 3. По данным рисунка найдите ОК, если RO = 20.

OM, ON – серед. перп.;

1) О – точка пересечения серединных перпендикуляров ⇒ ОК – серединный перпендикуляр (по свойству серединных перпендикуляров треугольника);

2) ОМ – серединный перпендикуляр ⇒ RO = PO = 20 (свойство серединного перпендикуляра к отрезку);

3) ОК – серединный перпендикуляр ⇒ ΔРОК – прямоугольный ⇒ ОК = (по свойству катета прямоугольного треугольника, лежащего против угла 30°).

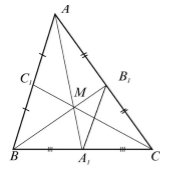
Пример 4. По данным рисунка найти угол МСВ1?

1) Продлим СМ до пересечения с АВ, АВ∩СС1 = С1,

М – точка пересечения биссектрис треугольника ⇒ СС1 – биссектриса треугольника АВС (по свойству биссектрис треугольника);

2) Рассмотрим ΔАВМ: ∠АМВ + ∠ВАМ + ∠АВМ = 180° ⇒ ∠ВАМ + ∠АВМ = 180° — 128° = 52°;

3) ВВ1, АА1 – биссектрисы ΔАВС ⇒ ∠А = 2∠ВАМ, ∠В = 2∠АВМ;

4) По теореме о сумме углов треугольника: ∠С = 180° — (∠А + ∠В) = 180° — (2∠ВАМ + 2∠АВМ) = 180° — 2(∠ВАМ + ∠АВМ) = 180° — 2 ⋅ 52° = 76°;

5) СС1 – биссектриса ∠С ⇒ ∠МСВ1 = ∠С : 2 = 38°.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Четыре замечательные точки треугольника

Подбор материалов по теме «Четыре замечательные точки треугольника» для учителей математики.

Просмотр содержимого документа
«Четыре замечательные точки треугольника»

Четыре замечательные точки треугольника

1. Точка пересечения медиан треугольника

2. Точка пересечения биссектрис треугольника

3. Точка пересечения серединных перпендикуляров треугольника

4. Точка пересечения высот треугольника

5. Пример задачи на использование 4 замечательных точек треугольника

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Точка пересечения медиан треугольника

Теорема 1 О пересечении медиан треугольника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1 начиная с вершины

. Доказательство. Рассмотрим треугольник ABC, где AA1, BB1, CC1 его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию A1B1 (Рис. 1).

Медианы треугольника По теореме 1, AB||A1B1 и AB=2A1B1, следовательно, ∠ABB1=∠BB1A1, ∠BAA1=∠AA1B1. Значит треугольники ABM и A1B1M подобны по первому признаку подобия треугольников. Тогда Аналогично доказывается, что

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство. Рассмотрим треугольник ABC, где AM, BP, CK его биссектрисы. Пусть точка O — точка пересечения биссектрис и AM и BP. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 3 Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. По теореме 3, имеем: OX=OZ, OX=OY. Следовательно, OY=OZ. Значит точка O равноудалена от сторон угла ACB и, значит, лежит на его биссектрисе CK. Теорема доказана.

Точка пересечения серединных перпендикуляров треугольника

Теорема 4
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство. Пусть дан треугольник ABC, n, m, p его серединные перпендикуляры. Пусть точка O — точка пересечения серединных перпендикуляров и n и m (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 5 Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: OB=OC, OB=OA. Следовательно, OA=OC. Значит точка O равноудалена от концов отрезка AC и, значит, лежит на его серединном перпендикуляре p. Теорема доказана.

Точка пересечения высот треугольника

Теорема 6 Высоты треугольника или их продолжения пересекаются в одной точке.
Доказательство. Рассмотрим треугольник ABC, где AA1, BB1, CC1 его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник A2B2C2 (рис. 4).

Рисунок 4. Высоты треугольника Так как AC2BC и B2ABC параллелограммы с общей стороной, то AC2=AB2, то есть точка A — середина стороны C2B2. Аналогично, получаем, что точка B — середина стороны C2A2, а точка C — середина стороны A2B2. Из построения мы имеем, что CC1⊥A2B2, BB1⊥A2C2, AA1⊥C2B2. Следовательно, AA1, BB1, CC1 — серединные перпендикуляры треугольника A2B2C2. Тогда, по теореме 4, имеем, что высоты AA1, BB1, CC1 пересекаются в одной точке. Теорема доказана.
Пример задачи на использование 4 замечательных точек треугольника Пример 1 Серединные перпендикуляры к сторонам AB и AC треугольника ABC пересекаются в точке D стороны BC. Докажите, что а) точка D — середина стороны BC. б) ∠A=∠B+∠C Решение. Изобразим рисунок.

Рисунок 5. а) По теореме 4, все серединные перпендикуляры пересекаются в точке D. Следовательно, D — основание серединного перпендикуляра к стороне BC. Значит точка D — середина стороны BC. б) Так как X и D — середины сторон, то XD — средняя линия треугольника. Тогда, по теореме о средней линии треугольника XD||AC. Значит,∠A=∠DXB, как соответственные углы. Значит, ∠A=900. Тогда∠B+∠C=1800−∠A=1800−900=900=∠A ч. т. д.

Информация взята с сайта биржи Автор24: https://avtor24.ru/spravochniki/matematika/okruzhnost/chetyre_zamechatelnye_tochki_treugolnika/ .

Замечательные точки треугольника — точки, местоположение которых не зависит от того, в каком порядке берутся стороны треугольника. Замечательными точками треугольника являются точки пересечения
Точка пересечения медиан треугольника (центроид;) , точка пересечения биссектрис
Треугольника (— инцентр (центр вписанной окружности)); , точка пересечения серединных перпендикуляров к сторонам треугольника (центр описанной окружности) , точка пересечения высот (или их продолжений) треугольника ( ортоцентр) ;

Замечательными точками треугольника являются

Медиан — центроид, центр тяжести (масс);

Биссектрис — инцентр или центр вписанной окружности;

Антибиссектрис — центр антибиссектрис;

Биссектрис внешних углов — центр вневписанной окружности;

Серединных перпендикуляров — центр описанной окружности;

Симедиан — точка Лемуана;

Биссектрис серединного треугольника (его инцентра) — Центр Шпикера;

Кливеров треугольника — также Центр Шпикера;

Трех (или даже двух) окружностей, построенных, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, — две точки Аполлония;

Отрезков, соединяющих вершины треугольника:

c точками касания противоположных сторон и вписанной окружности — точка Жергонна;

c точками касания противоположных сторон и вневписанных окружностей — точка Нагеля;

c соответствующими свободными вершинами равносторонних треугольников, построенных на сторонах треугольника (наружу) — первая точка Торричелли;

с соответствующими свободными вершинами правильных треугольников, построенных внутрь треугольника — вторая точка Торричелли;

c соответствующими свободными вершинами треугольников, подобных исходному треугольнику и построенных на его сторонах — точки Брокара;

Минимаксные точки треугольника[править | править вики-текст]

Минимаксными (экстремальными) точками треугольника назовем точки, имеющие наименьшие суммы степеней расстояний до сторон или вершин треугольника или какие-либо другие параметры треугольника [1] .

Минимаксными точками треугольника являются:

Точка пересечения трех медиан, имеющая наименьшую сумму квадратов расстояний до вершин треугольника.

Точка пересечения трех медиан треугольника является единственной точкой треугольника такой, что проведенные через нее три чевианы разделяют своими концами стороны треугольника на шесть отрезков. При этом произведение длин трех из этих шести отрезков, не имеющих общих концов, максимально. [2]

Точка Торричелли (первая), имеющая наименьшую сумму расстояний до вершин треугольника с углами не более 120 градусов.

точка Лемуана, имеющая наименьшую сумму квадратов расстояний до сторон треугольника.

Основания высот остроугольного треугольника образуют ортотреугольник, имеющий наименьший периметр из всех треугольников, вписанных в данный треугольник.

Изо-точки и изо-прямые треугольника[править | править вики-текст]

Основная статья: Замечательные прямые треугольника

Изо-точками являются точки треугольника, дающие какие-либо равные параметры трех треугольников, которые образуются при соединении изо-точки отрезками с тремя вершинами треугольника [3] . В результате образуется фигура типа «глаз дракона» (см. рис.)

Изо-точки треугольника, образующие фигуру типа «глаз дракона«[править | править вики-текст]

Изо-точками треугольника такого типа являются:

ортоцентр (дает три треугольника с равными радиусами трех описанных около них окружностей),

точка пересечения медиан (дает три треугольника с равными площадями)

инцентр (дает три треугольника с равными высотами)

центр описанной окружности (дает три равнобедренных треугольника с равными парами сторон),

точка равных периметров P или изопериметрическая точка (дает три треугольника с равными периметрами, см. http://faculty.evansville.edu/ck6/tcenters/recent/isoper.html ),

точка Торричелли(первая) (дает три треугольника с равными тупыми углами в 120 градусов).

Изо-точки треугольника, образующие фигуру типа «Трилистник (узел)«[править | править вики-текст]

Стилизованный трилистник (узел)

Изо-точками треугольника такого типа являются (см. рис.):

Центр Шпикера S является точкой пересечений прямых AX, BY и CZ, где XBC, YCA и ZAB подобные, равнобедренные и одинаково расположенные, построенные на сторонах треугольника ABC снаружи, имеющие один и тот же угол у основания <displaystyle mathrm ,[mathrm ,(A/2)mathrm ,(B/2)mathrm ,(C/2)]> [4] .

Первая точка Наполеона <displaystyle N_> , как и центр Шпикера, является точкой пересечений прямых AX, BY и CZ, где XBC, YCA и ZAB подобные, равнобедренные и одинаково расположенные, построенные на сторонах треугольника ABC снаружи, имеющие один и тот же угол у основания 30 градусов.

Изо-точки треугольника, образующие фигуру типа «Цветок традесканции»[править | править вики-текст]

Стилизованный цветок традесканции

Изо-точки треугольника, образующие фигуру типа «Цветок традесканции» (см. рис.) следующие:

точка пересечения медиан образует тремя малыми отрезками чевиан три четырехугольника с равными площадями.

точка пересечения биссектрис образует тремя перпендикулярами к трем сторонам треугольника три четырехугольника—дельтоида с двумя одинаковыми у всех смежными сторонами. Другая пара равных смежных сторон в общем случае у всех разная. У всех трех дельтоидов есть пара равных противоположных углов в 90 градусов. Они — вписанно-описанные четырехугольники.

Три окружности, проведенные внутри треугольника через точку Микеля, пересекают стороны треугольника в трех точках. Три хорды, проведенные через точку Микеля и три точки пересечения трех окружностей с тремя разными сторонами треугольника, образуют равные углы со сторонами.

Другие изо-точки треугольника[править | править вики-текст]

Изо-точками треугольника такого типа являются:

точка Лемуана (точка равных антипараллелей) — точка обладающая свойством: проведенные через неё 3 антипараллели (линии, антипараллельные 3 сторонам треугольника) дают внутри треугольника 3 отрезка равной длины.

точка равных параллелей (Equal Parallelians Point) [5] . В некотором смысле аналогична точке Лемуана. Точка обладает свойством: проведенные через неё 3 параллели (линии, параллельные 3 сторонам треугольника) дают внутри треугольника 3 отрезка равной длины.

точки Скутина — точки равных чевиан треугольника. Теорема Скутина утверждает, что три отрезка прямых или чевианы, проведенные внутри треугольника через три его вершины и через любой фокус описанного эллипса Штейнера, равны между собой. Эти фокусы часто называют точками Скутина.

Изо-прямые[править | править вики-текст]

Изо-прямыми (изо-линиями) треугольника являются прямые, которые разрезают данный треугольник на два треугольника, имеющие какие-либо равные параметры [3] . Изо-прямыми треугольника являются:

Медиана треугольника делит противоположную сторону пополам и разрезает треугольник на два треугольника с равными площадями.

Биссектриса (Биссектор) треугольника делит пополам угол, из вершины которого она выходит.

Высота треугольника пересекает противоположную сторону (или её продолжение) под прямым углом (то есть образует два равных угла со стороной по обе стороны от неё) и разрезает треугольник на два треугольника с равными (прямыми) углами.

Симедиана — геометрическое место точек внутри треугольника, выходящее из одной вершины, дающее два равных отрезка, антипараллельных двум сторонам, пересекающимся в этой вершине, и ограниченных тремя сторонами.

Кливер треугольника разбивает периметр пополам. Кливер треугольника — это отрезок, один конец которого находится в середине одной из сторон треугольника, второй конец находится на одной из двух оставшихся сторон. Кроме того, кливер параллелен одной из биссектрис угла. Каждый из кливеров проходит через центр масс периметра треугольника ABC, так что все три кливера пересекаются в центре Шпикера.

Также разбивает периметр пополам отрезок, соединяющий точку касания стороны треугольника и вневписанной окружности с вершиной, противоположной данной стороне. Три таких отрезка треугольника, проведенные из трех его вершин, пересекаются в точке Нагеля. Иными словами, этот отрезок есть чевиана точки Нагеля. (Чевиану точки Нагеля в английской литературе иногда называют сплиттером (splitter) или делителем пополам периметра [6] . К сплиттеру они относят и кливер).

Эквалайзер (equalizer) или уравниватель (выравниватель) — отрезок прямой, разрезающий треугольник на две фигуры одновременно равных площадей и периметров [7]

Немного об эквалайзере (equalizer). Любая прямая (эквалайзер), проходящая через треугольник и делящая площадь треугольника и периметр пополам, проходит через центр вписанной окружности. Таких прямых может существовать три, две или одна. [8]

Замечание об изо-прямых треугольника[править | править вики-текст]

В английской литературе вводится понятие бисекции (Bisection), как разделение чего-либо на две равные части. Например равнобедренного треугольника на два равных, отрезка прямой на два равных, плоского угла на два равных. Соответствующие линии будут являться частным случаем изо-прямых (изо-линий) треугольника. [9]

Прямые n[править | править вики-текст]

Важным частным случаем изо-прямых являются так называемые прямые n треугольника. Прямая n треугольника, исходящая из его вершины, делит противоположную сторону в отношении n-ых степеней прилежащих к ней двух сторон [10] . Важными частными случаями прямых n являются:

прямая кубов (n=3)

Для прямых n треугольника очень просто найти в общем виде некоторые свойства. Например, для прямой n изогонально сопряженной будет прямая (2-n), а изотомически сопряженной будет прямая минус n.

Замечание[править | править вики-текст]

Барицентрические координаты центра, записанные через стороны (или тригонометрические функции углов) треугольника, дают возможность перевести многие задачи о центрах треугольника на алгебраический язык. Например, выяснить, задают ли два определения один и тот же центр или лежат ли три данных центра на одной прямой.

Можно использовать и трилинейные координаты центра, очень просто связанные с барицентрическими координатами. Однако, например, изогонально сопряженные точки в трилинейных координатах выражаются проще.

Вариации и обобщения[править | править вики-текст]

Рассматривают пары центров. Например

Точки Аполлония. Для всякого невырожденного треугольника АВС можно построить окружность Аполлония к стороне АВ, проходящую через точку С. Окружности, построенные таким образом к трём сторонам, будут пересекаться в двух точках — внутренней и внешней Аполлония соответственно.

Недавно открытые точки (центры) треугольника[править | править вики-текст]

Источник: http://faculty.evansville.edu/ck6/tcenters/index.html Указаны интернет-сайты, где эти точки описаны и показаны на английском языке. http://faculty.evansville.edu/ck6/tcenters/recent/exeter.html

Иффа точка конгруэнтности (Yff Center of Congruence) http://faculty.evansville.edu/ck6/tcenters/recent/yffcc.html

Перспектор Госсарда (Gossard Perspector) http://faculty.evansville.edu/ck6/tcenters/recent/gosspersp.html

Средняя точка (Mittenpunkt=mid point =http://faculty.evansville.edu/ck6/tcenters/class/mitten.html)

Точки Аджима—Мальфатти −1-я и 2-я (1ST AND 2ND Ajima-Malfatti Points) http://faculty.evansville.edu/ck6/tcenters/recent/ajmalf.html

Точка Аполлониуса — не путать с точками Аполлония (Apollonius Point) http://faculty.evansville.edu/ck6/tcenters/recent/apollon.html

Точки Бейли (Bailey Point) http://faculty.evansville.edu/ck6/tcenters/recent/bailey.html

Точки Гофштадтера (Hofstadter Points) http://faculty.evansville.edu/ck6/tcenters/recent/hofstad.html

Изо-скелизерно-конгруэнтная точка (Congruent Isoscelizers Point)

Точки Морлея −1-я и 2-я, связанные с треугольником Морлея (1ST AND 2ND Morley Centers)http://faculty.evansville.edu/ck6/tcenters/recent/morley.html

Точка Пэрри (Parry Point) http://faculty.evansville.edu/ck6/tcenters/recent/parry.html

Точка равного периметра и равного обхода (Isoperimetric Point and Equal Detour Point) http://faculty.evansville.edu/ck6/tcenters/recent/isoper.html

Точки равных параллелей (Equal Parallelians Point) http://faculty.evansville.edu/ck6/tcenters/recent/eqparal.html

Точка Шиффлера (Schiffler Point) http://faculty.evansville.edu/ck6/tcenters/recent/schiff.html

Точка Экзетера (Exeter Point) http://faculty.evansville.edu/ck6/tcenters/recent/exeter.html

Литература[править | править вики-текст]

Энциклопедия для детей. Т. 11. Математика/Глав. ред. М. Д. Аксёнова. — М.: Аванта+, 2001. — 688 c.: ил.

А. Г. Мякишев. Элементы геометрии треугольника. — М.: МЦНМО, 2002.

Примечания[править | править вики-текст]

↑ Стариков В.Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 97.

↑ Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. задача на с. 12.

↑ Перейти к: 1 2 Стариков В.Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические нау-ки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 37, левая колонка, последний абзац.

↑ Weisstein, Eric W. Kiepert Hyperbola (англ.) на сайте Wolfram MathWorld.

↑ (Equal Parallelians Point// http://faculty.evansville.edu/ck6/tcenters/recent/eqparal.html.

↑ Kodokostas, Dimitrios (2010), «Triangle equalizers«, Mathematics Magazine Т. 83 (2): 141–146.

↑ Dimitrios Kodokostas Triangle Equalizers // Mathematics Magazine. — 2010. — Вып. 83, April. — С. 141-146..

↑ Bisection (Деление пополам, англ. яз.)/ https://en.wikipedia.org/wiki/Bisection#Area_bisectors_and_area-perimeter_bisectors_of_a_triangle.

↑ Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. задача на с. 120-125. параграфы 109-113.

Ссылки[править | править вики-текст]

Замечательные точки треугольника

Энциклопедия центров треугольника (англ.)

🌟 Видео

Уравнения стороны треугольника и медианыСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

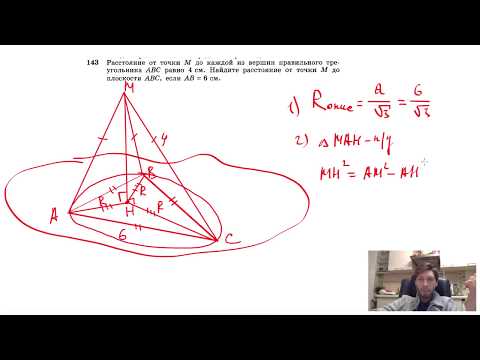
№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

Геометрия 8 класс : Решение задач. 4 замечательные точкиСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

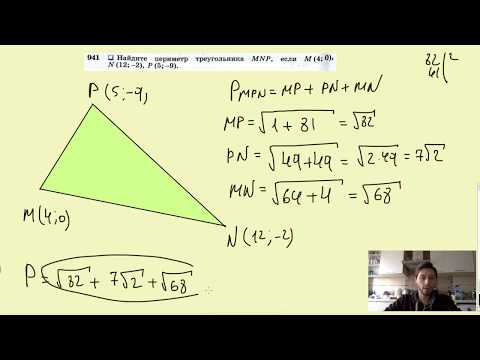
№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Виды треугольниковСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Построение следов плоскостиСкачать

Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать