Треугольник паскаля до 100 (3 видео) | Курс школьной геометрии

Содержание

Треугольник Паскаля
Натуральные степени бинома x + y
Свойства треугольника Паскаля
Определения
Написать разложение вида: (x + y) 7
Треугольник Паскаля
Построение треугольника Паскаля
Суть треугольной последовательности
История открытия
Удивительные свойства
Построение треугольника Паскаля
Примеры из реальной жизни
Подсчет количества способов
Определение вероятности
Заключение
🔥 Видео

Видео:Треугольник ПаскаляСкачать

Треугольник Паскаля

Треугольником Паскаля называется бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.

№	Треугольник Паскаля
0	1
1	1 1
2	1 2 1
3	1 3 3 1
4	1 4 6 4 1
5	1 5 10 10 5 1
6	1 6 15 20 15 6 1
…	…

Треугольник Паскаля можно получить из таблицы натуральных степеней бинома x + y

Натуральные степени бинома x + y

№	Степень	Разложение в сумму одночленов
0	(x + y) 0 =	1
1	(x + y) 1 =	1x + 1y
2	(x + y) 2 =	1x 2 + 2xy + 1y 2
3	(x + y) 3 =	1x 3 + 3x 2 y + 3xy 2 + 1y 3
4	(x + y) 4 =	1x 4 + 4x 3 y + 6x 2 y 2 + 4xy 3 + 1y 4
5	(x + y) 5 =	1x 5 + 5x 4 y + 10x 3 y 2 + 10x 2 y 3 + 5xy 4 + 1y 5
6	(x + y) 6 =	1x 6 + 6x 5 y + 15x 4 y 2 + 20x 3 y 3 + 15x 2 y 4 + 6xy 5 + 1y 6
…	…	…

Свойства треугольника Паскаля

Сумма чисел n-ной строки (отсчет ведется с нуля) треугольника Паскаля равна 2 n . Действительно, при переходе от каждой строки к следующей сумма членов удваивается, а для нулевой строки она равна 2 0 =1 .
Все строки треугольника Паскаля симметричны. Потому что при переходе от каждой строки к следующей свойство симметричности сохраняется, а нулевая строка симметрична.
Каждое число в треугольнике Паскаля равно C_n k , где n — номер строки, k — номер (отсчет ведется с нуля) элемента в строке.
Каждое число треугольника Паскаля, уменьшенное на единицу, равно сумме всех чисел, заполняющих параллелограмм, ограниченный диагоналями, на пересечении которых находится этот элемент.
Вдоль диагоналей, параллельных сторонам треугольника, выстроены треугольные числа, тетраэдрические числа и т.д.
Если посчитать для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел, то получится соответствующее число Фибоначчи.

Определения

Треугольными числами называется количество шаров, которые можно выложить в виде равностороннего треугольника.

Тетраэдрическими числами называется количество шаров, которые можно выложить в виде правильного тетраэдра.

Последовательность f₁ = f₂ = 1 , f_n = f_n−1 + f_n−2 при n>2 называется последовательностью Фибоначчи, а ее члены — числами Фибоначчи.

Написать разложение вида: (x + y) 7

Воспользовавшись строкой треугольника Паскаля с номером 6 и применив основное свойство треугольника Паскаля, получим строку с номером 7:

Видео:ТРЕУГОЛЬНИК ПАСКАЛЯ 😊 ЧАСТЬ I #shorts #математика #егэ #задачи #задачаналогику #егэ2022 #огэ2022Скачать

Треугольник Паскаля

Если говорить о треугольнике Паскаля, то его можно охарактеризовать как бесконечную таблицу. В данной таблице используются биномиальные коэффициенты. А сама таблица представлена в виде треугольника. Чтобы произвести расчет, можно использовать калькулятор, где указывается только количество строк. При самостоятельном расчете потребуется время и знание формул.

Как уже говорилось, данный треугольник представляет собой таблицу, начинается которая с нулевой строки. Вершина таблицы и боковые стороны каждой строки имеют единицы. Остальные числа (в середине) равны сумме 2-ух чисел, которые находятся в предыдущей строке (над ними).

В данном случае используются натуральные степени бинома: х+у
Для нулевой строки: (x + y)° =
Для первой: (x + y)¹ =
Для второй: (x + y)² =
И так далее.
Если разложить в сумму одночленов, получим для нулевой: 1
Для первой: 1x + 1y
Для второй: 1x² + 2xy + 1y²
Треугольника Паскаля, для расчетов используется формула:

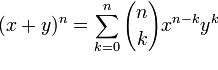
где

Видео:Треугольник ПаскаляСкачать

Построение треугольника Паскаля

Треугольник Паскаля — элегантный математический треугольник, представляющий собой бесконечную таблицу биноминальных коэффициентов. Таблица иллюстрирует скрытые соотношения между числами, которые естественным образом возникают в теории чисел, комбинаторике, теории вероятностей и алгебре.

Видео:#26. Треугольник Паскаля как пример работы вложенных циклов | Python для начинающихСкачать

Суть треугольной последовательности

Число 1 — важное число, а 11? Любопытно, что 11 × 11 = 121, 11 × 11 × 11 = 1331, а 11 × 11 × 11 × 11 = 14641. Если выстроить эти числа сверху вниз и представить их в виде отдельных цифр, то получится интересная формация:

Эти цифры — первые строки знаменитого треугольника Паскаля. Далее таблица строится по следующему принципу: по краям записываются единицы, а внутри ряда числа формируются путем суммы цифр, расположенных рядом выше слева и справа от искомых. Данная таблица знаменита в математике своей элегантностью, симметрией и неожиданными связями между числами. Связи таблицы с другими математическими сферами превратили треугольник Паскаля в Священный Грааль математики.

Видео:Треугольник ПаскаляСкачать

История открытия

Считается, что таблица была открыта Блезом Паскалем в 1653 году, однако происхождение формации гораздо древнее. Первое упоминание о бесконечной треугольной таблице встречается в трудах индийских математиков 10-го века, а наиболее полная информация о треугольнике представлена в работе китайского математика Шицзе, опубликованной в 1303 году. Однако и Шизце лишь упомянул о формации, создателем же треугольника Паскаля считается китайский ученый Ян Хуэй, поэтому в Китае таблица биноминальных коэффициентов носит название «треугольник Хуэя».

Видео:4.3 Треугольник Паскаля 1. "Поколение Python": курс для продвинутых. Курс StepikСкачать

Удивительные свойства

Симметрия — очевидное свойство треугольника Паскаля. Если из верхней единицы провести вертикальную прямую, то числа справа и слева будут симметричны. Диагонали треугольника также симметричны. Диагонали вообще обладают рядом уникальных свойств. Если первая диагональ, как восточная, так и западная, представляет собой ряд сплошных единиц, то вторая — ряд натуральных чисел, третья — ряд треугольных чисел, а четвертая — тетраэдрических.

Треугольные числа (1, 3, 6, 10…) — это числа, при помощи которых строятся плоские треугольники. Простыми словами, если в двухмерной игре вы захотите составить треугольник из круглых элементов, то вам понадобится выстроить элементы в количестве, советующему треугольным числам: сначала 6 кругов, потом 3, потом 1.
Тетраэдрические числа (1, 4, 10, 20…) используются для построения объемных тетраэдров. Проще говоря, если вам понадобится сложить пушечные ядра аккуратной пирамидой, то в основании вам потребуется уложить 20 ядер, на них еще 10, сверху 4 и увенчать пирамиду одним верхним ядром.

Кроме того, если в треугольнике Паскаля четные числа заменить единицами, а нечетные — нулями, то получится треугольник Серпинского — известный фрактал, построенный польским математиком в начале 20 века.

Треугольник Паскаля также имеет удивительную связь с алгеброй. Если мы разложим бином Ньютона вида (1 + x) 2 , то получим 1 + 2x + x 2 . Если же это будет (1 + x) 3 , то в результате мы получим 1 + 3x + 3x 2 + x 3 . Если присмотреться, то биноминальные коэффициенты — это ни что иное как числа из соответствующего ряда треугольника Паскаля.

Видео:Бином Ньютона и треугольник Паскаля | Учитель года Москвы — 2020Скачать

Построение треугольника Паскаля

Треугольник Паскаля — это бесконечная таблица элементов. При помощи нашего калькулятора вы можете построить таблицу любой размерности, однако не рекомендуется использовать слишком большие числа (n>100), так как столь огромные таблицы не имеют практического применения, а онлайн-калькулятор строит их слишком долго. Помимо элегантных свойств, используемых для решения биноминальных уравнений или построения тетраэдрических последовательностей, таблица Паскаля находит применение в комбинаторике.

Видео:Зачем нужен треугольник Паскаля (спойлер: для формул сокращённого умножения)Скачать

Примеры из реальной жизни

Подсчет количества способов

Если на кафедре работают 7 математиков, и троих из них нужно отправить на городскую олимпиаду, то сколькими способами можно это сделать? Это стандартная задача на комбинаторику, в котором важен порядок элементов, то есть вариант «Сидоров, Иванов и Петров» отличается от варианта «Иванов, Петров, Сидоров», хотя выбранная группа математиков одна и та же. Такая ситуация возникает в случае, если преподаватели должны участвовать в разных конкурсах. При «ручном» решении нам пришлось бы использовать стандартные формулы для комбинаторики, однако проще воспользоваться свойствами треугольника Паскаля.

Для ответа на вопрос нам достаточно построить треугольник с n = 10, найти седьмой ряд и третье число в нем. Таким образом, существует 35 способов объединить математиков для поездки на олимпиаду.

Определение вероятности

В корзине лежит 20 шаров, пронумерованных от 1 до 20. Наугад мы берем 3 шара. Какова вероятность, что мы вытащим шары с номерами 5, 12 и 13? Для решения этой задачи нам потребуется построить треугольник Паскаля с n = 20, после чего найти двадцатый ряд и третье число в нем. Вытащить три шара можно 1140 способами. Вероятность наступления нашего события составит 3 из 1140.

Видео:Числа сочетаний. Треугольник Паскаля | Ботай со мной #059 | Борис Трушин |Скачать

Заключение

Треугольник Паскаля — простая таблица, которая таит в себе огромное количество математических тайн. Члены рядов связаны с биноминальными коэффициентами, совершенными числами, числами Фибоначчи, тетраэдрическими и треугольными числами. Используйте наш калькулятор для построения сетки необходимой вам размерности для решения самых разных математических задач.